Dạng 1: Nhận biết và chứng minh đường thẳng vuông góc với mặt phẳng có đáp án
-
136 lượt thi
-
10 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, điểm I và H lần lượt là trung điểm của AB và BC. Trên đoạn CI và SA lần lượt lấy hai điểm M, N sao cho MC = 2MI, NA = 2NS. Biết SH ⊥ (ABC). Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: B
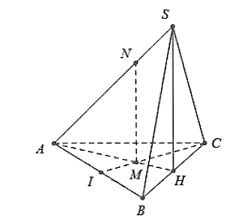
Do điểm M thuộc đường trung tuyến CI và MC = 2MI
M là trọng tâm tam giác ABC nên AH giao CI tại M
Ta có:
Do đó, MN // SH
Mặt khác, SH ⊥ (ABC) nên MN ⊥ (ABC). Suy ra MN vuông góc với AB.
Câu 2:
Cho hình chóp S.ABC, các tam giác ABC và SBC là các tam giác nhọn. Gọi H và K lần lượt là trực tâm của tam giác ABC và SBC. Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: A
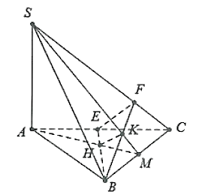
Giả sử AH vuông góc với BC tại M
Ta có:
BC vuông góc với AM
BC vuông góc với SA
Do đó, BC ⊥ (SAM).
Câu 3:
Cho hình chóp S.ABC, các tam giác ABC và SBC là các tam giác nhọn. Gọi H và K lần lượt là trực tâm của tam giác ABC và SBC. Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: C
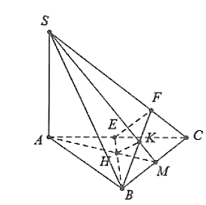
Do H là trực tâm của tam giác ABC nên BH vuông góc với AC
Mặt khác, SA vuông góc với (ABC) nên BH vuông góc với SA
Do đó, BH vuông góc với (SAC)
⇒ BH vuông góc với SC
Lại có: BK vuông góc với SC
Do đó, SC vuông góc với (BHK).Câu 4:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt bên SAB là tam giác đều, SCD là tam giác vuông cân đỉnh S. Gọi I, J lần lượt là trung điểm của AB và CD. Gọi H là hình chiếu của S lên IJ, đường thẳng SH vuông góc với mặt phẳng nào sau đây?
Xem đáp án
Đáp án đúng là: C
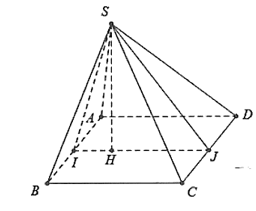
Ta có: ∆SAB đều cạnh a nên
Tứ giác IBCJ là hình chữ nhật nên IJ = BC = a
∆SCD là tam giác vuông cân đỉnh S ⇒ SJ = =
Do đó, SJ2 + SI2 = IJ2 = a2 ⇒ ∆SIJ vuông tại S.
Do ∆SCD cân tại S nên SJ ⊥ CD
Do AB // CD ⇒ SJ ⊥ (SAB)
Chứng minh tương tự ta có SI ⊥ (SCD)
⇒ SI ⊥ CD
Mà CD ⊥ IJ ⇒ CD ⊥ (SIJ) ⇒ CD ⊥ SH
Do SH ⊥ IJ ⇒ SH ⊥ (ABCD).
Câu 5:
Khẳng định nào sau đây là sai?
Xem đáp án
Đáp án đúng là: B
Đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong (α) thì d ⊥ (α), từ đó suy ra d vuông góc mọi đường thẳng nằm trong (α). Vậy đáp án B sai, do thiếu yếu tố cắt nhau.
Câu 6:
Cho hình chóp S.ABCD có SA ⊥ (ABCD) và tam giác ABC vuông ở B, AH là đường cao của ∆SAB. Khẳng định nào sau đây sai?
Xem đáp án
Đáp án đúng là: D
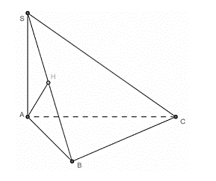
Do SA ⊥ (ABCD) nên SA ⊥ (ABC)
Do tam giác ABC vuông tại B nên BC ⊥ AB, do SA ⊥ (ABCD) nên BC ⊥ SA.
Do đó, BC ⊥ (SAB)
Do BC ⊥ (SAB) nên AH ⊥ BC, do AH là đường cao nên AH ⊥ SB, do đó, AH ⊥ (SBC).
Vậy A, B, C đúng. Do đó đáp án D là sai.
Câu 7:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi O và có SA = SC, SB = SD. Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: D
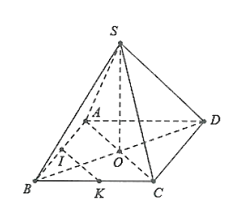
Do SA = AC nên ∆SAC cân tại S có trung tuyến SO đồng thời là đường cao, từ đó suy ra SO ⊥ AC.
Tương tự ta có: SO ⊥ BD
Do đó, SO ⊥ (ABCD).
Câu 8:
Cho tứ diện ABCD có AB = AC và DB = DC. Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: D
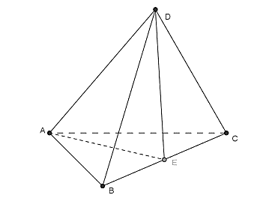
Gọi E là trung điểm của BC. Khi đó ta có:
.
Câu 9:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết SA = SC và SB = SD. Khẳng định nào sau đây sai?
Xem đáp án
Đáp án đúng là: B
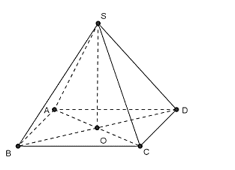
Tam giác SAC cân tại S có SO là trung tuyến.
Do đó, SO cũng là đường cao nên SO vuông góc với AC.
Tam giác SBD cân tại S có SO là trung tuyến.
Do đó, SO cũng là đường cao nên SO vuông góc với BD.
Từ đó suy ra: SO ⊥ (ABCD).
Do ABCD là hình thoi nên CD không vuông góc với BD. Do đó, CD không vuông góc với (SBD).
Câu 10:
Cho hình chóp S.ABC có cạnh SA ⊥(ABC) và đáy ABC là tam giác cân ở C. Gọi H và K lần lượt là trung điểm của AB và SB. Khẳng định nào sau đây là sai?
Xem đáp án
Đáp án đúng là: D
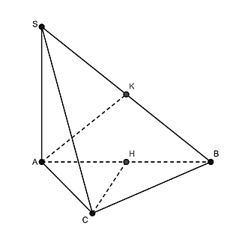
Do tam giác ABC cân tại C nên CH ⊥ AB.
Suy ra: CH ⊥ (SAB).
Vậy A, B, C đúng nên D sai.