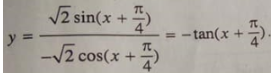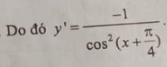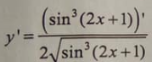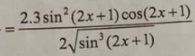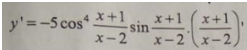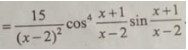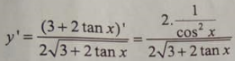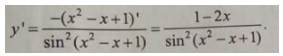23 câu hỏi trắc nghiệm thuộc Trắc nghiệm Đại số và Giải tích 11 Bài 3 (Có đáp án): Đạo hàm của các hàm số lượng giác

Câu 1:

$\underset{x \to 0}{l i m} \frac{\sin 2 x}{\tan 3 x}$ bằng:

A. 1

B. 0

C. 2/3

D. 3/2

$\begin{array}{l} \lim_{x \to 0} \frac{\sin 2 x}{\tan 3 x} = \lim_{x \to 0} \frac{\sin 2 x . c os 3x}{\sin 3 x} \\ = \lim_{x \to 0} \frac{2. \frac{\sin 2 x}{2 x} . c os3x}{3. \frac{\sin 3 x}{3 x}} = \frac{2.1. c os0}{3.1} = \frac{2}{3} \end{array}$

ĐÁP ÁN C

Câu 2:

Đạo hàm của hàm số: $y = \sin 2 x + \cos \frac{x^{2} + 1}{2} - \tan \sqrt{x}$ bằng biểu thức nào sau đây?

A. $\cos 2 x - \sin \frac{x^{2} + 1}{2} - \frac{1}{\cos^{2} \sqrt{x}}$

B. $2 \cos 2 x - x \sin \frac{x^{2} + 1}{2} - \frac{1}{2 \sqrt{x} \cos^{2} \sqrt{x}}$

C. $- 2 \cos x + x \sin \frac{x^{2} + 1}{2} - \frac{1}{2 \sqrt{x} \cos^{2} \sqrt{x}}$

D. $2 \cos 2 x + x \sin \frac{x^{2} + 1}{2} - \frac{1}{2 \sqrt{x} \cos^{2} \sqrt{x}}$

Xem đáp án

$y' = c os2x. (2x)' - sin \frac{x {}^{2}+ 1}{2} . (\frac{x {}^{2}+ 1}{2})' - \frac{1}{{cos}^{2} \sqrt{x}} . (\sqrt{x})'$

Chọn B

Câu 3:

Đạo hàm của hàm số: $y = \sin 2 x \cos^{4} x - c o t \frac{1}{x^{2}} - \sin 2 x . \sin^{4} x$ bằng biểu thức nào sau đây?``

A. $\cos 2 x . 4 \cos^{2} x + \frac{1}{\sin^{2} \frac{1}{x^{2}}} - \cos 2 x 4 \sin^{3} x$

B. $2 \cos 4 x + \frac{2}{x^{3} \sin^{2} \frac{1}{x^{2}}}$

C. $2 \cos 4 x + \frac{2}{x \sin^{2} \frac{1}{x^{2}}}$

D. $2 \cos 4 x - \frac{2}{x^{3} \sin^{2} \frac{1}{x^{2}}}$

Xem đáp án

Chú ý. Rút gọn trước khi tính đạo hàm

Câu 4:

$\underset{x \to 0}{l i m} \frac{\tan x - \sin x}{x^{3}}$ bằng:

A. 0

B. 2

C. 1/2

D. 1/4

Xem đáp án

Chọn C

Câu 5:

Đạo hàm của hàm số: $y = \frac{\sin x + \cos x}{\sin x - \cos x}$

bằng biểu thức nào sau đây?

A. $\frac{\cos x + \sin x}{\sin x - \cos x}$

B. $\frac{- 1}{\cos^{2} (x + \frac{π}{4})}$

C. $\frac{1}{\cos^{2} (x + \frac{π}{4})}$

D. $\frac{- 2 \sin x}{{(\sin x - \cos x)}^{2}}$

Xem đáp án

Chọn B

Câu 6:

Đạo hàm của hàm số: $y = \sqrt{\sin^{3} (2 x + 1)}$ bằng biểu thức nào sau đây?

A. $\frac{3 \sin^{2} (2 x + 1)}{2 \sqrt{\sin^{3} (2 x + 1)}}$

B. $3 \sqrt{s in (2 x + 1)} \cos (2 x + 1)$

C. $\frac{3 \sin^{2} 2 (2 x + 1)}{2 \sqrt{\sin^{3} (2 x + 1)}}$

D. $3 \sqrt{\sin (2 x + 1)}$

Xem đáp án

Chọn B

Câu 7:

Đạo hàm của hàm số: $y = \cos^{5} \frac{x + 1}{x - 2}$ bằng biểu thức nào sau đây?

A. $\frac{15}{{(x - 2)}^{2}} \cos^{4} \frac{x + 1}{x - 2} \sin \frac{x + 1}{x - 2}$

B. $- 5 \cos^{4} \frac{x + 1}{x - 2} \sin \frac{x + 1}{x - 2}$

C. $5 \cos^{4} \frac{x + 1}{x - 2} \sin \frac{x + 1}{x - 2}$

D. $- \frac{15}{{(x - 2)}^{2}} \cos^{4} \frac{x + 1}{x - 2} \sin \frac{x + 1}{x - 2}$

Xem đáp án

Chọn A

Câu 8:

Đạo hàm của hàm số $y = \sqrt{3 + 2 \tan x}$ bằng biểu thức nào sau đây?

A. $\frac{1}{\sin^{2} x \sqrt{3 + 2 \tan x}}$

B. $\frac{- 1}{\sin^{2} x \sqrt{3 + 2 \tan x}}$

C. $\frac{1}{\cos^{2} x \sqrt{3 + 2 \tan x}}$

D. $\frac{- 1}{\cos^{2} x \sqrt{3 + 2 \tan x}}$

Xem đáp án

Chọn C

Câu 9:

Đạo hàm của hàm số $y = c o t (x^{2} - x + 1)$ bằng biểu thức nào sau đây?

A. $\frac{2 x - 1}{\sin^{2} (x^{2} - x + 1)}$

B. $- \frac{2 x - 1}{\sin (x^{2} - x + 1)}$

C. $\frac{2 x - 1}{c o s^{2} (x^{2} - x + 1)}$

D. $\frac{1 - 2 x}{\sin^{2} (x^{2} - x + 1)}$

Xem đáp án

Chọn D

Câu 10:

Đạo hàm của hàm số y = cos⁶x + sin⁴x. cos²x + sin²x. cos⁴x + sin⁴x – sin²x bằng biểu thức nào sau đây?

A. $- 6 \cos^{5} x \sin x$

B. $6 \cos^{5} x \sin x$

C. $6 \sin^{5} x \cos x$

D. $6 \cos^{5} x$

Xem đáp án

Chọn A

y = cos6 x+ sin2xcos2x(sin2x + cos2x) + sin4x - sin2x

= cos6x + sin2x(1 - sin2x).1 + sin4x - sin2x

= cos6x + sin2x - sin4x + sin4x - sin2x

= cos6x

Do đó : y' = -6cos5xsinx.

Câu 11:

Cho hàm số:

$f (x) = \frac{\sin 3 x}{3} - \cos x - \sqrt{3} (\sin x - \frac{\cos 3 x}{3})$ . Giải phương trình f’(x)=0

A. $x = \frac{π}{12} + k π hoặc x = \frac{- 3 π}{8} + k \frac{π}{2} (k \in ℤ)$

B. $x = \frac{- π}{12} + k π hoặc x = \frac{- 3 π}{8} + k \frac{π}{2} (k \in ℤ)$

C. $x = - \frac{π}{12} + k π hoặc x = \frac{3 π}{8} + k \frac{π}{2} (k \in ℤ)$

D. $x = \frac{π}{12} + k π hoặc x = \frac{3 π}{8} + k \frac{π}{2} (k \in ℤ)$

Xem đáp án

Chọn C

Câu 12:

Tính đạo hàm của hàm số sau $y = {(\frac{\sin x}{1 + \cos x})}^{3}$

A. $\frac{\sin^{2} x}{{(1 + \cos x)}^{3}}$

B. $\frac{3 \sin^{2} x}{{(1 + \cos x)}^{2}}$

C. $\frac{2 \sin^{2} x}{{(1 + \cos x)}^{2}}$

D. $\frac{3 \sin^{2} x}{{(1 + \cos x)}^{3}}$

Xem đáp án

Chọn D.

Bước đầu tiên ta áp dụng công thức ${(u^{α})}^{/}$ với $u = \frac{\sin x}{1 + \cos x}$

$y' = 3 {(\frac{\sin x}{1 + \cos x})}^{2} . {(\frac{\sin}{1 + \cos x})}^{/}$

Tính :

$\begin{array}{l} {(\frac{\sin x}{1 + \cos x})}^{/} \\ = \frac{{(\sin x)}^{/} (1 + \cos x) - {(1 + \cos x)}^{/} . \sin x}{{(1 + \cos x)}^{2}} \\ = \frac{\cos x (1 + \cos x) + \sin^{2} x}{{(1 + \cos x)}^{2}} \end{array}$

$\begin{array}{l} = \frac{\cos x + \cos^{2} x + \sin^{2} x}{{(1 + \cos x)}^{2}} \\ = \frac{cosx + 1}{{(1 + c osx)}^{2}} = \frac{1}{1 + \cos x} \end{array}$ .

Vậy

$\begin{array}{l} y' = 3 {(\frac{\sin x}{1 + \cos x})}^{2} . \frac{1}{1 + \cos x} \\ = \frac{3 \sin^{2} x}{{(1 + \cos x)}^{3}} \end{array}$

Câu 13:

Tính đạo hàm của hàm số sau $y = \sin (\cos^{2} x . \tan^{2} x)$

A. $y' = \cos (\cos^{2} x . \tan^{2} x) (- \sin 2 x \tan^{2} x + 2 \tan x)$

B. $y' = \cos (\cos^{2} x . \tan^{2} x) (\sin 2 x \tan^{2} x + \tan x)$

C. $y' = \cos (\cos^{2} x . \tan^{2} x) (- \sin 2 x \tan^{2} x + \tan x)$

D. $y' = \cos (\cos^{2} x . \tan^{2} x) (\sin 2 x \tan^{2} x + 2 \tan x)$

Xem đáp án

Chọn A

Áp dụng ${(\sin u)}^{/},$ với $u = \cos^{2} x \tan^{2} x$

$y' = \cos (\cos^{2} x . \tan^{2} x) . {(\cos^{2} x . \tan^{2} x)}^{/} .$

Tính ${(\cos^{2} x . \tan^{2} x)}^{/},$ bước đầu sử dụng ${(u . v)}^{/},$ sau đó sử dụng ${(u^{α})}^{/} .$

$\begin{array}{l} {(\cos^{2} x . \tan^{2} x)}^{/} \\ = {(\cos^{2} x)}^{/} . \tan^{2} x + {(\tan^{2} x)}^{/} . \cos^{2} x \end{array}$

$= 2 \cos x {(\cos x)}^{/} \tan^{2} x + 2 \tan x {(\tan x)}^{/} \cos^{2} x$

$\begin{array}{l} = - 2 \sin x \cos x \tan^{2} x + 2 \tan x \frac{1}{\cos^{2} x} \cos^{2} x \\ = - \sin 2 x \tan^{2} x + 2 \tan x . \end{array}$

Vậy $y' = \cos (\cos^{2} x . \tan^{2} x) (- \sin 2 x \tan^{2} x + 2 \tan x)$

Câu 14:

Tính đạo hàm của hàm số sau $y = \frac{\sin 2 x + \cos 2 x}{2 \sin 2 x - \cos 2 x} .$

A. $\frac{6}{{(2 \sin 2 x - \cos 2 x)}^{2}}$

B. $\frac{- 6}{{(\sin 2 x - \cos 2 x)}^{2}}$

C. $\frac{6}{{(2 \sin 2 x - \cos x)}^{2}}$

D. $\frac{- 6}{{(2 \sin 2 x - \cos 2 x)}^{2}}$

Xem đáp án

Chọn D

$y' = \frac{{(\sin 2 x + \cos 2 x)}^{/} . (2 \sin 2 x - \cos 2 x) - {(2 \sin 2 x - \cos 2 x)}^{/} . (\sin 2 x + \cos 2 x)}{{(2 \sin 2 x - \cos 2 x)}^{2}}$

$\begin{array}{l} y' = \frac{(2 \cos 2 x - 2 \sin 2 x) (2 \sin 2 x - \cos 2 x) - (4 \cos 2 x + 2 \sin 2 x) (\sin 2 x + \cos 2 x)}{{(2 \sin 2 x - \cos 2 x)}^{2}} \\ = \frac{4. c {os2x. sin2x - 2cos}^{2} 2 x - 4 \sin^{2} 2 x + 2. \sin 2 x . c os2x}{{(2 \sin 2 x - \cos 2 x)}^{2}} \\ - \frac{{( 4cos2x . sin2x + 4cos}^{2} 2 x + 2 \sin^{2} 2 x + 2 \sin 2 x . c os2x}{{( 2 \sin 2 x - c os2x)}^{2}} \end{array}$

$\begin{array}{l} y' = \frac{- 6 \cos^{2} 2 x - 6 \sin^{2} 2 x}{{(2 \sin 2 x - \cos 2 x)}^{2}} \\ = \frac{- 6}{{(2 \sin 2 x - \cos 2 x)}^{2}} \end{array}$

Câu 15:

Tính đạo hàm của hàm số sau $y = \sin^{2} (\cos (\tan^{4} 3 x))$

A. $y' = \sin (2 \cos (\tan^{4} 3 x)) . (\sin (\tan^{4} 3 x)) .4 \tan^{3} 3 x . (1 + \tan^{2} 3 x) .3$

B. $y' = \sin (2 \cos (\tan^{4} 3 x)) . (\sin (\tan^{4} 3 x)) . \tan^{3} 3 x . (1 + \tan^{3} 3 x) .$

C. $y' = - \sin (2 \cos (\tan^{4} 3 x)) . (\sin (\tan^{4} 3 x)) .4 \tan^{3} 3 x . (1 + \tan^{2} 3 x) .3$

D. $y' = \sin (2 \cos (\tan^{4} 3 x)) . (\sin (\tan^{4} 3 x)) .4 \tan^{3} 3 x$

Xem đáp án

Chọn C

Đầu tiên áp dụng ${(u^{α})}^{/},$ với $u = \sin (\cos (\tan^{4} 3 x))$

$y' = 2 \sin (\cos (\tan^{4} 3 x)) . {[\sin (\cos (\tan^{4} 3 x))]}^{/}$

Sau đó áp dụng ${(\sin u)}^{/},$ với $u = \cos (\tan^{4} 3 x)$

$y' = 2 \sin (\cos (\tan^{4} 3 x)) . \cos (\cos (\tan^{4} 3 x)) . {(\cos (\tan^{4} 3 x))}^{/}$

Áp dụng ${(\cos u)}^{/},$ với $u = \tan^{4} 3 x .$

$y' = - \sin (2 \cos (\tan^{4} 3 x)) . (\sin (\tan^{4} 3 x)) . {(\tan^{4} 3 x)}^{/} .$

Áp dụng ${(u^{α})}^{/},$ với $u = \tan 3 x$

$y' = - \sin (2 \cos (\tan^{4} 3 x)) . (\sin (\tan^{4} 3 x)) .4 \tan^{3} 3 x . {(\tan 3 x)}^{/} .$

$y' = - \sin (2 \cos (\tan^{4} 3 x)) . (\sin (\tan^{4} 3 x)) .4 \tan^{3} 3 x . (1 + \tan^{2} 3 x) . {(3 x)}^{/} .$

$y' = - \sin (2 \cos (\tan^{4} 3 x)) . (\sin (\tan^{4} 3 x)) .4 \tan^{3} 3 x . (1 + \tan^{3} 3 x) .3$

Câu 16:

Hàm số $y = \frac{\sin x - x \cos x}{\cos x + x \sin x}$ có đạo hàm bằng

A. $\frac{- x^{2} . \sin 2 x}{{(\cos x + x \sin x)}^{2}}$

B. $\frac{- x^{2} . \sin^{2} x}{{(\cos x + x \sin x)}^{2}}$

C. $\frac{- x^{2} . \cos 2 x}{{(\cos x + x \sin x)}^{2}}$

D. ${(\frac{x}{\cos x + x \sin x})}^{2}$

Xem đáp án

Chọn D

$\begin{array}{l} y^{'} = \frac{{(s in x - x \cos x)}^{'} (\cos x + x \sin x) - {(\cos x + x \sin x)}^{'} (s in x - x \cos x)}{{(\cos x + x \sin x)}^{2}} \\ = \frac{(cos x - \cos x + x . s inx) (\cos x + x \sin x) - (- \sin x + \sin x + x . c osx) (s in x - x \cos x)}{{(\cos x + x \sin x)}^{2}} \\ = \frac{x \sin x (\cos x + x \sin x) - x \cos x (s in x - x \cos x)}{{(\cos x + x \sin x)}^{2}} \\ = \frac{x^{2} \sin^{2} x + x^{2} \cos^{2} x}{{(\cos x + x \sin x)}^{2}} = {(\frac{x}{\cos x + x \sin x})}^{2} \end{array}$

Câu 17:

Cho hàm số $y = \cot^{2} \frac{x}{4}$ . Khi đó nghiệm của phương trình $y' = 0$ là

A. $π + k 2 π$

B. $2 π + k 4 π$

C. $2 π + k π$

D. $π + k π$

Xem đáp án

Chọn B.

$\begin{array}{l} y^{'} = {(\cot^{2} \frac{x}{4})}^{'} \\ = 2 \cot \frac{x}{4} {(\cot \frac{x}{4})}^{'} \\ = - \frac{1}{2} \cot \frac{x}{4} (1 + \cot^{2} \frac{x}{4}) \end{array}$

$\begin{array}{l} y' = 0 \\ \Leftrightarrow \frac{1}{2} \cot \frac{x}{4} (1 + \cot^{2} \frac{x}{4}) = 0 \end{array}$

$\begin{array}{l} \Leftrightarrow \cot \frac{x}{4} = 0 \\ \Leftrightarrow \frac{x}{4} = \frac{π}{2} + k π \\ \Leftrightarrow x = 2 π + k 4 π, k \in ℤ \end{array}$

Câu 18:

Hàm số $y = 2 \sqrt{\sin x} - 2 \sqrt{\cos x}$ có đạo hàm là:

A. $y' = \frac{1}{\sqrt{\sin x}} - \frac{1}{\sqrt{\cos x}}$

B. $y' = \frac{1}{\sqrt{\sin x}} + \frac{1}{\sqrt{\cos x}}$

C. $y' = \frac{\cos x}{\sqrt{\sin x}} + \frac{\sin x}{\sqrt{\cos x}}$

D. $y' = \frac{\cos x}{\sqrt{\sin x}} - \frac{\sin x}{\sqrt{\cos x}}$

Xem đáp án

Chọn C

$\begin{array}{l} y' = 2 (\sqrt{\sin x})' - 2 (\sqrt{\cos x})' \\ = 2. \cos x . \frac{1}{2 \sqrt{\sin x}} + 2 \sin x \frac{1}{2 \sqrt{\cos x}} \end{array}$

$= \frac{\cos x}{\sqrt{\sin x}} + \frac{\sin x}{\sqrt{\cos x}}$

Câu 19:

Tính đạo hàm của hàm số sau $y = 2 \sin^{2} 4 x - 3 \cos^{3} 5 x$

A. $y' = \sin 8 x + \frac{45}{2} c o s 5 x . \sin 10 x$

B. $y' = 8 \sin 8 x + \frac{5}{2} c o s 5 x . \sin 10 x$

C. $y' = 8 \sin x + \frac{45}{2} c o s 5 x . \sin 10 x$

D. $y' = 8 \sin 8 x + \frac{45}{2} c o s 5 x . \sin 10 x$

Xem đáp án

Chọn D.

Bước đầu tiên áp dụng ${(u + v)}^{/}$

$y' = {(2 \sin^{2} 4 x)}^{/} - 3 {(\cos^{3} 5 x)}^{/}$

Tính ${(\sin^{2} 4 x)}^{/}$ : Áp dụng ${(u^{α})}^{/}$ , với $u = \sin 4 x,$ ta được:

$\begin{array}{l} {(\sin^{2} 4 x)}^{/} = 2 \sin 4 x . {(\sin 4 x)}^{/} \\ = 2 \sin 4 x . \cos 4 x {(4 x)}^{/} \\ = 8. \sin 4 x . c os4x = 4 \sin 8 x . \end{array}$

Tương tự:

$\begin{array}{l} {(\cos^{3} 5 x)}^{/} = 3 \cos^{2} 5 x . {(\cos 5 x)}^{/} \\ = 3 \cos^{2} 5 x . (- \sin 5 x) . {(5 x)}^{/} \end{array}$

$\begin{array}{l} = - 15 \cos^{2} 5 x . \sin 5 x \\ = \frac{- 15}{2} c o s 5 x . \sin 10 x . \end{array}$

Kết luận: $y' = 8 \sin 8 x + \frac{45}{2} c o s 5 x . \sin 10 x$

Câu 20:

Tính đạo hàm của hàm số sau: $y = {(2 + \sin^{2} 2 x)}^{3}$ .

A. $y' = 6 \sin 4 x {(2 + \sin^{2} 2 x)}^{3} .$

B. $y' = 3 \sin 4 x {(2 + \sin^{2} 2 x)}^{2} .$

C. $y' = s i n 4 x {(2 + \sin^{2} 2 x)}^{2} .$

D. $y' = 6 \sin 4 x {(2 + \sin^{2} 2 x)}^{2} .$

Xem đáp án

Chọn D

Áp dụng ${(u^{α})}^{/}$ , với $u = 2 + \sin^{2} 2 x .$

$\begin{array}{l} y' = 3 {(2 + \sin^{2} 2 x)}^{2} {(2 + \sin^{2} 2 x)}^{/} \\ = 3 {(2 + \sin^{2} 2 x)}^{2} {(\sin^{2} 2 x)}^{/} . \end{array}$

Tính ${(\sin^{2} 2 x)}^{/},$ áp dụng ${(u^{α})}^{/},$ với $u = \sin 2 x .$

$\begin{array}{l} {(\sin^{2} 2 x)}^{/} = 2. \sin 2 x {(\sin 2 x)}^{/} \\ = 2. \sin 2 x . \cos 2 x {(2 x)}^{/} \\ = 2 \sin 4 x . \end{array}$

$\Rightarrow y' = 6 \sin 4 x {(2 + \sin^{2} 2 x)}^{2} .$

Câu 21:

Đạo hàm của hàm số $y = \sqrt{2 + \tan (x + \frac{1}{x})}$ là:

A. $y^{'} = \frac{1}{2 \sqrt{2 + \tan (x + \frac{1}{x})}} \cdot$

B. $y^{'} = \frac{1 + \tan^{2} (x + \frac{1}{x})}{2 \sqrt{2 + \tan (x + \frac{1}{x})}} \cdot$

C. $y^{'} = \frac{1 + \tan^{2} (x + \frac{1}{x})}{2 \sqrt{2 + \tan (x + \frac{1}{x})}} . (1 - \frac{1}{x^{2}}) .$

D. $y^{'} = \frac{1 + \tan^{2} (x + \frac{1}{x})}{2 \sqrt{2 + \tan (x + \frac{1}{x})}} . (1 + \frac{1}{x^{2}}) .$

Xem đáp án

Chọn C

$\begin{array}{l} y^{'} = \frac{{[2 + \tan (x + \frac{1}{x})]}^{'}}{2 \sqrt{2 + \tan (x + \frac{1}{x})}} \\ = \frac{1 + \tan^{2} (x + \frac{1}{x})}{2 \sqrt{2 + \tan (x + \frac{1}{x})}} \cdot {(x + \frac{1}{x})}^{'} \end{array}$

$= \frac{1 + \tan^{2} (x + \frac{1}{x})}{2 \sqrt{2 + \tan (x + \frac{1}{x})}} \cdot (1 - \frac{1}{x^{2}})$

Câu 22:

Đạo hàm của hàm số $y = \cot^{2} (\cos x) + \sqrt{\sin x - \frac{π}{2}}$ là

A. $y' = - 2 \cot (\cos x) \frac{1}{\sin^{2} (\cos x)} + \frac{\cos x}{2 \sqrt{\sin x - \frac{π}{2}}} .$

B. $y' = 2 \cot (\cos x) \frac{1}{\sin^{2} (\cos x)} . \sin x + \frac{\cos x}{2 \sqrt{\sin x - \frac{π}{2}}} .$

C. $y' = - 2 \cot (\cos x) \frac{1}{\sin^{2} (\cos x)} + \frac{\cos x}{\sqrt{\sin x - \frac{π}{2}}} .$

D. $y' = 2 \cot (\cos x) \frac{1}{\sin^{2} (\cos x)} . \sin x - \frac{\cos x}{\sqrt{\sin x - \frac{π}{2}}} .$

Xem đáp án

Chọn B

$\begin{array}{l} y^{'} = 2 \cot (\cos x) . {(\cot (\cos x))}^{'} + \frac{{(\sin x - \frac{π}{2})}^{'}}{2 \sqrt{s in x - \frac{π}{2}}} \\ = 2 \cot (\cos x) . \frac{- 1}{\sin^{2} (\cos x)} . ( c osx)' + \frac{cosx}{2 \sqrt{s in x - \frac{π}{2}}} \\ = 2 \cot (\cos x) . \frac{1}{\sin^{2} (\cos x)} . \sin x + \frac{\cos x}{2 \sqrt{\sin x - \frac{π}{2}}} \end{array}$

Câu 23:

Hàm số $y = \frac{\cos x}{2 \sin^{2} x}$ có đạo hàm bằng:

A. $- \frac{1 + \cos^{2} x}{2 \sin^{3} x}$

B. $- \frac{1 + \sin^{2} x}{2 \sin^{3} x}$

C. $\frac{1 + \sin^{2} x}{2 \sin^{3} x}$

D. $\frac{3 \sin^{2} x}{{(1 + \cos x)}^{3}}$

Xem đáp án

Chọn A

$\begin{array}{l} y^{'} = {(\frac{\cos x}{2 \sin^{2} x})}^{'} \\ = \frac{2 \sin^{2} x {(\cos x)}^{'} - (2 \sin^{2} x)' . \cos x}{4 \sin^{4} x} \\ = \frac{- 2 \sin^{3} x - 2.2 \sin x . \cos x . \cos x}{4 \sin^{4} x} \end{array}$

$\begin{array}{l} = - \frac{\sin^{2} x + 2 {cos}^{2} x}{2 \sin^{3} x} \\ = - \frac{(\sin^{2} x + c {os}^{2} x) + {cos}^{2} x}{2 \sin^{3} x} \\ = - \frac{1 + {cos}^{2} x}{2 \sin^{3} x} \end{array}$