Giải SBT Toán 11 Cánh diều Bài Góc lượng giác. Giá trị lượng giác của góc lượng giác
Giải SBT Toán 11 Cánh diều Bài Góc lượng giác. Giá trị lượng giác của góc lượng giác
-
238 lượt thi
-
18 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho lục giác đều ABCDEF nội tiếp trong đường tròn lượng giác (thứ tự đi từ A đến các đỉnh theo chiều ngược chiều kim đồng hồ). Tính số đo của các góc lượng giác (OA, OB), (OA, OC), (OA, OD), (OA, OE), (OA, OF).
 Xem đáp án
Xem đáp án
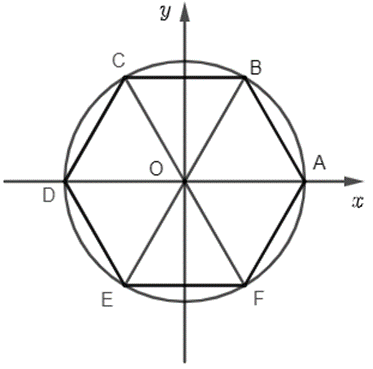
Vì ABCDEF là lục giác đều nên
\(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = \frac{{360^\circ }}{6} = 60^\circ = \frac{\pi }{3}\).
Khi đó, ta có:
\(\left( {OA,OB} \right) = \frac{\pi }{3} + k2\pi \);
\(\left( {OA,OC} \right) = \frac{\pi }{3} + \frac{\pi }{3} + k2\pi = \frac{{2\pi }}{3} + k2\pi \);
\(\left( {OA,OD} \right) = \pi + k2\pi \);
\(\left( {OA,OE} \right) = - \frac{\pi }{3} - \frac{\pi }{3} + k2\pi = - \frac{{2\pi }}{3} + k2\pi \);
\(\left( {OA,OF} \right) = - \frac{\pi }{3} + k2\pi \).
Câu 2:
Cho \(\sin \alpha = \frac{1}{3}\) với \(\alpha \in \left( {\frac{\pi }{2};\pi } \right)\). Tính cos α, tanα, cot α.
 Xem đáp án
Xem đáp án
Vì \(\alpha \in \left( {\frac{\pi }{2};\pi } \right)\) nên cos α < 0.
Do đó từ sin2 α + cos2 α = 1, suy ra
\(\cos \alpha = - \sqrt {1 - {{\sin }^2}\alpha } = - \sqrt {1 - {{\left( {\frac{1}{3}} \right)}^2}} = - \frac{{2\sqrt 2 }}{3}\).
Khi đó, \[\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{\frac{1}{3}}}{{ - \frac{{2\sqrt 2 }}{3}}} = - \frac{1}{{2\sqrt 2 }} = - \frac{{\sqrt 2 }}{4}\];
\(\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{1}{{ - \frac{{\sqrt 2 }}{4}}} = - 2\sqrt 2 \).
Câu 3:
Cho cot x = – 3, \(\frac{\pi }{2} < x < \pi \). Tính sin x, cos x, tan x.
 Xem đáp án
Xem đáp án
Ta có: \(\tan x = \frac{1}{{\cot x}} = \frac{1}{{ - 3}} = - \frac{1}{3}\).
Áp dụng công thức \(1 + {\cot ^2}x = \frac{1}{{{{\sin }^2}x}}\), ta được \({\sin ^2}x = \frac{1}{{1 + {{\cot }^2}x}} = \frac{1}{{1 + {{\left( { - 3} \right)}^2}}} = \frac{1}{{10}}\).
Mà \(\frac{\pi }{2} < x < \pi \) nên sin x > 0. Suy ra \(\sin x = \frac{{\sqrt {10} }}{{10}}\).
Khi đó từ \(\cot x = \frac{{\cos x}}{{\sin x}}\), suy ra cos x = cot x . sin x = \( - 3.\frac{{\sqrt {10} }}{{10}} = - \frac{{3\sqrt {10} }}{{10}}\).
Câu 4:
Chứng minh rằng:
sin4 x + cos4 x = 1 − 2sin2 x cos2 x;
 Xem đáp án
Xem đáp án
VT = sin4 x + cos4 x
= (sin2 x)2 + (cos2 x)2 + 2sin2 x . cos2 x – 2sin2 x . cos2 x
= (sin2 x + cos2 x)2 – 2sin2 x . cos2 x
= 12 – 2sin2 x . cos2 x = 1 – 2sin2 x . cos2 x = VP (đpcm).
Câu 5:
Chứng minh rằng:
sin6 x + cos6 x = 1 – 3sin2 x cos2 x.
 Xem đáp án
Xem đáp án
VT = sin6 x + cos6 x
= (sin2 x)3 + (cos2 x)3
= (sin2 x + cos2 x)3 – 3sin2 x cos2 x(sin2 x + cos2 x)
= 13 – 3sin2 x cos2 x . 1
= 1 – 3sin2 x cos2 x (đpcm).Câu 6:
Cho tan x = − 2. Tính giá trị của biểu thức sau:
\(B = \frac{{2{{\sin }^2}x - 3\sin x\cos x - {{\cos }^2}x}}{{{{\sin }^2}x + \sin x\cos x}}\).
 Xem đáp án
Xem đáp án
Vì tan x xác định nên cos2 x khác 0. Chia cả tử và mẫu của B cho cos2 x ta được:
\(B = \frac{{2{{\sin }^2}x - 3\sin x\cos x - {{\cos }^2}x}}{{{{\sin }^2}x + \sin x\cos x}}\)\( = \frac{{2{{\tan }^2}x - 3\tan x - 1}}{{{{\tan }^2}x + \tan x}}\)\( = \frac{{2.{{\left( { - 2} \right)}^2} - 3.\left( { - 2} \right) - 1}}{{{{\left( { - 2} \right)}^2} + \left( { - 2} \right)}} = \frac{{13}}{2}\).
Câu 7:
Tính:
A = \({\cos ^2}\frac{\pi }{8} + {\cos ^2}\frac{{3\pi }}{8} + {\cos ^2}\frac{{5\pi }}{8} + {\cos ^2}\frac{{7\pi }}{8}\);
 Xem đáp án
Xem đáp án
Do \(\cos \frac{{7\pi }}{8} = \cos \left( {\pi - \frac{\pi }{8}} \right) = - \cos \left( { - \frac{\pi }{8}} \right) = - \cos \frac{\pi }{8}\);
\(\cos \frac{{5\pi }}{8} = \cos \left( {\pi - \frac{{3\pi }}{8}} \right) = - \cos \left( { - \frac{{3\pi }}{8}} \right) = - \cos \frac{{3\pi }}{8}\).
Nên A = \({\cos ^2}\frac{\pi }{8} + {\cos ^2}\frac{{3\pi }}{8} + {\cos ^2}\frac{{5\pi }}{8} + {\cos ^2}\frac{{7\pi }}{8}\)
= \({\cos ^2}\frac{\pi }{8} + {\cos ^2}\frac{{3\pi }}{8} + {\left( { - \cos \frac{{3\pi }}{8}} \right)^2} + {\left( { - \cos \frac{\pi }{8}} \right)^2}\)
\( = 2\left( {{{\cos }^2}\frac{\pi }{8} + {{\cos }^2}\frac{{3\pi }}{8}} \right)\)
\( = 2\left[ {{{\cos }^2}\frac{\pi }{8} + {{\sin }^2}\left( {\frac{\pi }{2} - \frac{{3\pi }}{8}} \right)} \right]\)
\( = 2\left( {{{\cos }^2}\frac{\pi }{8} + {{\sin }^2}\frac{\pi }{8}} \right) = 2.1 = 2\).
Câu 8:
Tính:
B = \(\sin \frac{\pi }{5} + \sin \frac{{2\pi }}{5} + ... + \sin \frac{{9\pi }}{5}\) (gồm 9 số hạng);
 Xem đáp án
Xem đáp án
Nhận thấy \(\sin \frac{{9\pi }}{5} = \sin \left( { - \frac{\pi }{5} + 2\pi } \right) = \sin \left( { - \frac{\pi }{5}} \right) = - \sin \frac{\pi }{5}\) nên \(\sin \frac{\pi }{5} + \sin \frac{{9\pi }}{5} = 0\).
Tương tự ta có: \(\sin \frac{{2\pi }}{5} + \sin \frac{{8\pi }}{5} = 0,\,\,\sin \frac{{3\pi }}{5} + \sin \frac{{7\pi }}{5} = 0,\,\,\sin \frac{{4\pi }}{5} + \sin \frac{{6\pi }}{5} = 0\).
Suy ra B = \(\sin \frac{\pi }{5} + \sin \frac{{2\pi }}{5} + ... + \sin \frac{{9\pi }}{5}\)
\[ = \left( {\sin \frac{\pi }{5} + \sin \frac{{9\pi }}{5}} \right) + \left( {\sin \frac{{2\pi }}{5} + \sin \frac{{8\pi }}{5}} \right) + \left( {\sin \frac{{3\pi }}{5} + \sin \frac{{7\pi }}{5}} \right) + \left( {\sin \frac{{4\pi }}{5} + \sin \frac{{6\pi }}{5}} \right) + \sin \frac{{5\pi }}{5}\]
\( = 0 + \sin \pi = 0\).
Câu 9:
Tính:
C = tan 1° . tan 2° . tan 3°. ... . tan 89° (gồm 89 thừa số).
 Xem đáp án
Xem đáp án
C = tan 1° . tan 2° . tan 3°. ... . tan 89°
= (tan 1° . tan 89°) . (tan 2° . tan 88°) . ... . (tan 44° . tan 46°) . tan 45°
= [tan 1° . cot(90° – 89°)] . [tan 2° . cot(90° – 88°)] . ... . [tan44° . cot(90° – 46°)] . tan 45°
= (tan 1° . cot 1°) . (tan 2° . cot 2°) . ... . (tan 44° . cot 44°) . tan 45°
= 1 . 1 . ... . 1 . 1
= 1.
Câu 10:
Chứng minh rằng trong tam giác ABC, ta có:
sin B = sin(A + C);
 Xem đáp án
Xem đáp án
Sử dụng định lí tổng 3 góc trong tam giác.
Do A + C = π – B nên sin(A + C) = sin(π – B) = sin B.
Vậy sin B = sin(A + C).
Câu 11:
 Xem đáp án
Xem đáp án
Sử dụng định lí tổng 3 góc trong tam giác.
Do A + B + 2C = A + B + C + C = π + C
Nên cos(A + B + 2C) = cos(π + C) = – cos C.
Suy ra cosC = – cos(A + B + 2C).
Câu 12:
Chứng minh rằng trong tam giác ABC, ta có:
\(\sin \frac{A}{2} = \cos \frac{{B + C}}{2}\);
 Xem đáp án
Xem đáp án
Ta có: \(\frac{{A + B + C}}{2} = \frac{\pi }{2}\), suy ra \(\frac{{B + C}}{2} = \frac{\pi }{2} - \frac{A}{2}\).
Nên \(\sin \frac{A}{2} = \cos \frac{{B + C}}{2}\).
Câu 13:
Chứng minh rằng trong tam giác ABC, ta có:
\(\tan \frac{{A + B - 2C}}{2} = \cot \frac{{3C}}{2}\).
 Xem đáp án
Xem đáp án
Ta có: \(\frac{{A + B - 2C}}{2} = \frac{{A + B + C - 3C}}{2} = \frac{{\pi - 3C}}{2} = \frac{\pi }{2} - \frac{{3C}}{2}\).
Suy ra \(\tan \frac{{A + B - 2C}}{2} = \cot \frac{{3C}}{2}\).
Câu 14:
Cho sin α + cos α = \(\frac{1}{3}\) với \( - \frac{\pi }{2} < \alpha < 0\). Tính:
A = sinα . cos α;
 Xem đáp án
Xem đáp án
Do sin α + cos α = \(\frac{1}{3}\) nên (sin α + cos α)2 = \({\left( {\frac{1}{3}} \right)^2} = \frac{1}{9}\).
Mà (sin α + cos α)2 = sin2 α + 2 sin α cos α + cos2 α = 1 + 2 sin α cos α.
Do đó, 1 + 2 sin α cos α = \(\frac{1}{9}\), suy ra A = sinα . cos α = \(\frac{{\frac{1}{9} - 1}}{2} = - \frac{4}{9}\).
Câu 15:
Cho sin α + cos α = \(\frac{1}{3}\) với \( - \frac{\pi }{2} < \alpha < 0\). Tính:
B = sin α – cos α;
 Xem đáp án
Xem đáp án
Ta có: B2 = (sin α – cos α)2 = 1 – 2 sin α cos α = \(1 - 2.\left( { - \frac{4}{9}} \right) = 1 + \frac{8}{9} = \frac{{17}}{9}\).
Do \( - \frac{\pi }{2} < \alpha < 0\) nên sin α < 0 và cos α > 0. Do đó sin α – cos α < 0.
Vậy B = \( - \frac{{\sqrt {17} }}{3}\).Câu 16:
Cho sin α + cos α = \(\frac{1}{3}\) với \( - \frac{\pi }{2} < \alpha < 0\). Tính:
C = sin³ α + cos³ α;
 Xem đáp án
Xem đáp án
Ta có:
C = sin³ α + cos³ α = (sin α + cos α)3 – 3 sin α cos α(sin α + cos α)
\( = {\left( {\frac{1}{3}} \right)^3} - 3.\left( { - \frac{4}{9}} \right).\left( {\frac{1}{3}} \right) = \frac{{13}}{{27}}\).
Câu 17:
Cho sin α + cos α = \(\frac{1}{3}\) với \( - \frac{\pi }{2} < \alpha < 0\). Tính:
D = sin4 α + cos4 α.
 Xem đáp án
Xem đáp án
Ta có:
D = sin4 α + cos4 α = 1 – 2sin2 α cos2 α (theo Bài 9a)
= 1 – 2 (sin α cos α)2 = \(1 - 2.{\left( { - \frac{4}{9}} \right)^2} = \frac{{49}}{{81}}\).Câu 18:
Một vòng quay Mặt Trời quay mỗi vòng khoảng 15 phút. Tại vị trí quan sát, bạn Linh thấy vòng quay chuyển động theo chiều kim đồng hồ. Khi vòng quay chuyển động được 10 phút, bán kính của vòng quay quét một góc lượng giác có số đo bằng bao nhiêu? (Tính theo đơn vị radian).
 Xem đáp án
Xem đáp án
Do vòng quay Mặt Trời quay mỗi vòng khoảng 15 phút và chuyển động theo chiều kim đồng hồ nên sau 15 phút, bán kính của vòng quay quét một góc lượng giác có số đo bằng – 2π (rad).
Do đó, sau 10 phút, bán kính của vòng quay quét một góc lượng giác có số đo bằng \(\frac{{ - 2\pi }}{{15}}.10 = \frac{{ - 4\pi }}{3}\) (rad).
