10 câu hỏi trắc nghiệm thuộc Dạng 1: Tính xác suất của biến cố giao của hai biến cố độc lập bằng cách sử dụng công thức nhân xác suất và sơ đồ hình cây có đáp án

Trắc nghiệm Toán 11 Bài 30. Công thức nhân xác suất cho hai biến cố độc lập có đáp án

Dạng 1: Tính xác suất của biến cố giao của hai biến cố độc lập bằng cách sử dụng công thức nhân xác suất và sơ đồ hình cây có đáp án

238 lượt thi
10 câu hỏi
60 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho A và B là hai biến cố độc lập. Biết $P (A) = \frac{1}{3}$ ; $P (B) = \frac{1}{4}$ . Xác suất của biến cố AB là

A. $\frac{7}{12}$

B. $\frac{5}{12}$

C. $\frac{1}{7}$

D. $\frac{1}{12}$

Xem đáp án

Đáp án đúng là: D

Áp dụng quy tắc nhân xác suất ta có $P (A B) = P (A) \cdot P (B) = \frac{1}{12}$ .

Câu 2:

Cho A và B là hai biến cố độc lập với nhau. Biết P(A) = 0,4 và P(B) = 0,6. Xác suất của các biến cố $\bar{A} B$ là

A. 0,24;

B. 0,36;

C. 0,16;

D. 0,2.

Xem đáp án

Đáp án đúng là: B

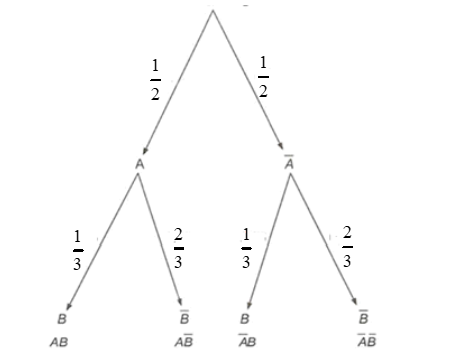
Ta có sơ đồ hình cây:

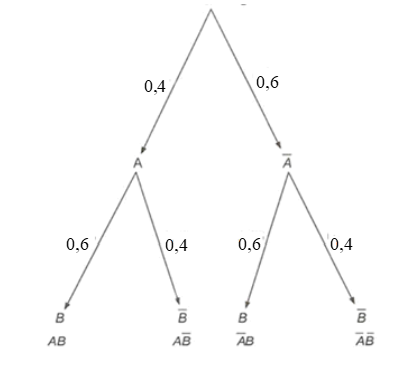
Cho A và B là hai biến cố độc lập với nhau. Biết P(A) = 0,4 và P(B) = 0,6. (ảnh 1)

Vì A và B là hai biến cố độc lập với nhau nên $\bar{A}$

và B cũng là hai biến cố độc lập.

Do đó $P (\bar{A} B) = P (\bar{A}) \cdot P (B) = 0, 6 \cdot 0, 6 = 0, 36 .$

Câu 3:

Cho A và B là hai biến cố độc lập với nhau. Biết P(A) = 0,4 và P(B) = 0,6. Xác suất của các biến cố $\bar{A} \bar{B}$ là

A. 0,24;

B. 0,16;

C. 0,76;

D. 0,36.

Xem đáp án

Đáp án đúng là: A

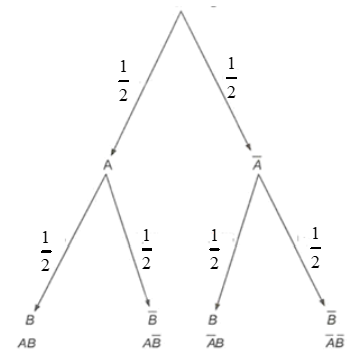
Ta có sơ đồ hình cây:

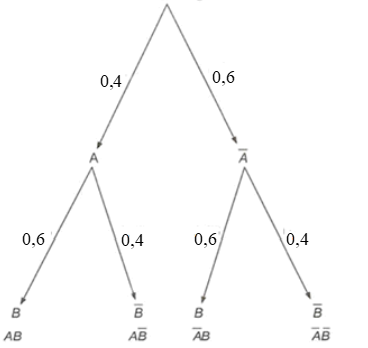
Vì A và B là hai biến cố độc lập với nhau nên $\bar{A}$ và $\bar{B}$ cũng là hai biến cố độc lập.

Do đó $P (\bar{A} \bar{B}) = P (\bar{A}) \cdot P (\bar{B}) = 0, 6 \cdot 0, 4 = 0, 24 .$

Câu 4:

An và Bình không quen biết nhau và học ở hai nơi khác nhau. Xác suất để An và Bình đạt điểm giỏi về môn Toán trong kì thi cuối năm tương ứng là 0,92 và 0,88. Xác suất để cả An và Bình đều không đạt điểm giỏi là

A. 0,8096;

B. 0,0096;

C. 0,3649;

D. 0,3597.

Xem đáp án

Đáp án đúng là: B

Gọi A là biến cố “An đạt điểm giỏi môn Toán” và B là biến cố “Bình đạt điểm giỏi môn Toán”.

Do đó A và B là hai biến cố độc lập, nên hai biến cố $\bar{A}$ và $\bar{B}$ độc lập.

Ta có $P (\bar{A}) = 1 - P (A) = 1 - 0, 92 = 0, 08$ và $P (\bar{B}) = 1 - P (B) = 1 - 0, 88 = 0, 12.$

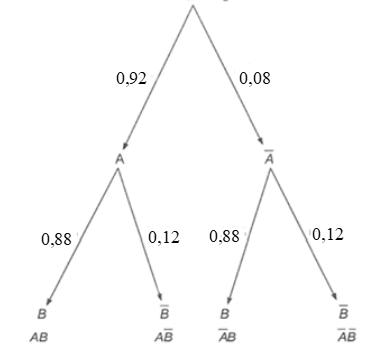
An và Bình không quen biết nhau và học ở hai nơi khác nhau. Xác suất để An và Bình đạt điểm giỏi (ảnh 1)

Ta có $\bar{A} \bar{B}$ là biến cố: "Cả An và Bình đều không đạt điểm giỏi môn Toán".

Do đó $P (\bar{A} \bar{B}) = P (\bar{A}) . P (\bar{B}) = 0, 08.0, 12 = 0, 0096$ .

Câu 5:

An và Bình không quen biết nhau và học ở hai nơi khác nhau. Xác suất để An và Bình đạt điểm giỏi về môn Toán trong kì thi cuối năm tương ứng là 0,92 và 0,88. Xác suất để cả An và Bình đều đạt điểm giỏi là

A. 0,8096;

B. 0,0096;

C. 0,3649;

D. 0,3597.

Xem đáp án

Đáp án đúng là: A

Gọi A là biến cố: "An đạt điểm giỏi về môn Toán" và B là biến cố: "Bình đạt điểm giỏi về môn Toán".

Ta có $P (\bar{A}) = 1 - P (A) = 1 - 0, 92 = 0, 08$ và $P (\bar{B}) = 1 - P (B) = 1 - 0, 88 = 0, 12.$

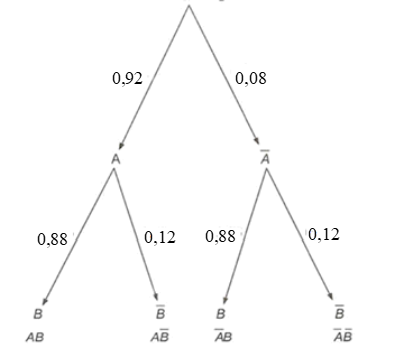
An và Bình không quen biết nhau và học ở hai nơi khác nhau. Xác suất để An và Bình đạt điểm giỏi về môn Toán (ảnh 1)

Ta có biến cố AB là: "Cả An và Bình đều đạt điểm giỏi môn Toán".

Do A và B là hai biến cố độc lập nên P(AB) = P(A).P(B) = 0,92.0,88 = 0,8096.

Câu 6:

Hai xạ thủ cùng bắn vào bia một cách độc lập với nhau. Xác suất bắn trúng bia của xạ thủ thứ nhất bằng $\frac{1}{2}$ , xác suất bắn trúng bia của xạ thủ thứ hai bằng $\frac{1}{3}$ . Xác suất của biến cố: “Xạ thủ thứ nhất bắn trúng bia, xạ thủ thứ hai bắn trật bia” là

A. $\frac{1}{4}$

B. $\frac{1}{3}$

C. $\frac{2}{3}$

D. $\frac{1}{2}$

Xem đáp án

Đáp án đúng là: B

Gọi A là biến cố: "Xạ thủ thứ nhất bắn trúng bia" và B là biến cố: "Xạ thủ thứ hai bắn trúng bia". Khi đó A, B, $\bar{A}$ , $\bar{B}$ là các biến cố độc lập đôi một với nhau.

Ta có: $P (\bar{A}) = 1 - P (A) = 1 - \frac{1}{2} = \frac{1}{2}$ , $P (\bar{B}) = 1 - P (B) = 1 - \frac{1}{3} = \frac{2}{3}$ .

Hai xạ thủ cùng bắn vào bia một cách độc lập với nhau. Xác suất bắn trúng bia của xạ thủ thứ nhất (ảnh 1)

Xét biến cố: “Xạ thủ thứ nhất bắn trúng bia, xạ thủ thứ hai bắn trật bia” là biến cố $A \bar{B} .$

Do A và $\bar{B} .$ là hai biến cố độc lập nên xác suất biến cố $A \bar{B}$ là:

$P (A \bar{B}) = P (A) . P (\bar{B}) = \frac{1}{2} . \frac{2}{3} = \frac{1}{3}$ .

Câu 7:

Gieo hai con xúc xắc cân đối và đồng chất. Gọi X là biến cố “Tích số chấm xuất hiện trên hai mặt con xúc xắc là một số lẻ”. Xác suất của X là

A. $\frac{1}{5}$

B. $\frac{1}{4}$

C. $\frac{1}{3}$

D. $\frac{1}{2}$

Xem đáp án

Đáp án đúng là: B

Gọi A là biến cố “con xúc xắc thứ nhất mặt lẻ”. $P (A) = \frac{1}{2}$ .

Gọi B là biến cố “con xúc xắc thứ hai mặt lẻ”. $P (B) = \frac{1}{2}$ .

Ta có: $P (\bar{A}) = 1 - P (A) = 1 - \frac{1}{2} = \frac{1}{2}$ , $P (\bar{B}) = 1 - P (B) = 1 - \frac{1}{2} = \frac{1}{2}$ .

Gieo hai con xúc xắc cân đối và đồng chất. Gọi X là biến cố “Tích số chấm xuất hiện trên hai mặt con xúc xắc là một số lẻ”. Xác suất của X là (ảnh 1)

Ta có AB là biến cố “Tích số chấm xuất hiện trên hai mặt con súc sắc là một số lẻ”.

Do A và B là hai biến cố độc lập nên $P (A B) = P (A) . P (B) = \frac{1}{4}$ .

Câu 8:

Một xạ thủ bắn lần lượt 2 viên đạn vào một bia. Xác suất trúng đích của viên thứ nhất và viên thứ hai lần lượt là 0,8 và 0,7. Biết rằng kết quả các lần bắn là độc lập với nhau. Xác suất của biến cố "Cả hai lần bắn đều trúng đích" là

A. 0,28;

B. 0,56;

C. 0,24;

D. 0,15.

Xem đáp án

Đáp án đúng là: B

Gọi A là biến cố “Lần 1 bắn trúng đích” và biến cố B “Lần 2 bắn trúng đích”.

Ta có sơ đồ hình cây:

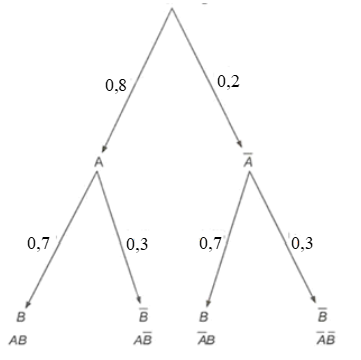
Một xạ thủ bắn lần lượt 2 viên đạn vào một bia. Xác suất trúng đích của viên thứ nhất và viên thứ hai lần lượt là 0,8 và 0,7. (ảnh 1)

Khi đó AB là biến cố “Cả hai lần bắn đều trúng đích".

Vì kết quả các lần bắn là độc lập với nhau nên P(AB) = P(A).P(B) = 0,8 . 0,7 = 0,56.

Câu 9:

Hai khẩu pháo cao xạ cùng bắn độc lập với nhau vào một mục tiêu. Xác suất bắn trúng mục tiêu lần lượt là $\frac{1}{4}$ và $\frac{1}{3}$ . Xác suất để mục tiêu bị trúng đạn là

A. $\frac{1}{4}$

B. $\frac{5}{12}$

C. $\frac{1}{2}$

D. $\frac{7}{12}$

Xem đáp án

Đáp án đúng là: C

Gọi A là biến cố “Khẩu pháo 1 bắn trúng”; $\bar{A}$ là biến cố “Khẩu pháo 1 không bắn trúng”.

B là biến cố “Khẩu pháo 2 bắn trúng”; $\bar{B} .$ là biến cố “Khẩu pháo 2 không bắn trúng”.

Ta có sơ đồ hình cây:

Hai khẩu pháo cao xạ cùng bắn độc lập với nhau vào một mục tiêu. Xác suất bắn trúng mục tiêu (ảnh 1)

Gọi M là biến cố “Mục tiêu bị bắn trúng”, khi đó $\bar{M}$ là biến cố “Mục tiêu không bị bắn trúng”. Ta có $\bar{M} = \bar{A} \bar{B} .$

Do A, B là hai biến cố độc lập nên $\bar{A}, \bar{B}$ cũng là hai biến cố độc lập

Do đó $P (\bar{M}) = P (\bar{A}) . P (\bar{B}) = \frac{3}{4} \cdot \frac{2}{3} = \frac{1}{2} .$

Vậy $P (M) = 1 - P (\bar{M}) = 1 - \frac{1}{2} = \frac{1}{2} .$

Câu 10:

Ba xạ thủ bắn vào mục tiêu một cách độc lập với nhau. Xác suất bắn trúng của xạ thủ thứ nhất, thứ hai và thứ ba lần lượt là 0,6; 0,7; 0,8. Xác suất để có ít nhất một xạ thủ bắn trúng là:

A. 0,188;

B. 0,024;

C. 0,976;

D. 0,812.

Xem đáp án

Đáp án đúng là: C

Gọi A₁ là biến cố “Xạ thủ thứ nhất bắn trúng”; A₂ là biến cố “Xạ thủ thứ hai bắn trúng”; A₃ là biến cố “Xạ thủ thứ ba bắn trúng”.

Ta có $P (\bar{A_{1}}) = 1 - 0, 6 = 0, 4$ ; $P (\bar{A_{2}}) = 1 - 0, 7 = 0, 3$ ; $P (\bar{A_{3}}) = 1 - 0, 8 = 0, 2$

Gọi A là biến cố “Có ít nhất một xạ thủ bắn trúng” thì $\bar{A}$ là biến cố “Không có xạ thủ nào bắn trúng”. Khi đó $\bar{A} = \bar{A_{1}} \bar{A_{2}} \bar{A_{3}} .$

Do A₁, A₂, A₃ là các biến cố đôi một độc lập nên các biến cố $\bar{A_{1}}, \bar{A_{2}}, \bar{A_{3}}$ là các biến cố đôi một độc lập.

Do đó $P (\bar{A}) = P (\bar{A_{1}}) . P (\bar{A_{2}}) . P (\bar{A_{3}}) = 0, 4.0, 3.0, 2 = 0, 024 .$

Vậy $P (A) = 1 - P (\bar{A}) = 1 - 0, 024 = 0, 976 .$

Bắt đầu thi ngay