10 câu hỏi trắc nghiệm thuộc Dạng 1: Xác định ảnh của một điểm, một đoạn thẳng, một tam giác, một đường tròn, … qua phép chiếu song song có đáp án

Câu 1:

Cho hình tứ diện có D, E, F, M, N, K lần lượt là trung điểm của các cạnh SA, SB, SC, AB, AC, BC (Như hình vẽ). Khẳng định nào dưới đây là đúng?

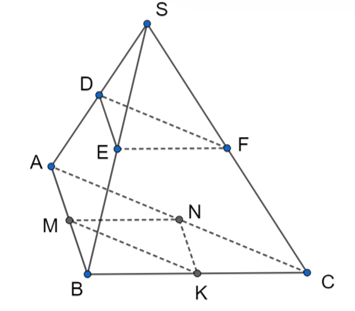
Cho hình tứ diện có D, E, F, M, N, K lần lượt là trung điểm của các cạnh SA, SB, SC, AB, AC, BC (Như hình vẽ). (ảnh 1)

A. Tam giác AMN là ảnh của tam giác DEF lên mặt phẳng đáy qua phép chiếu song song theo phương SB;

B. Tam giác BMK là ảnh của tam giác DEF lên mặt phẳng đáy qua phép chiếu song song theo phương SB;

C. Tam giác AMN là ảnh của tam giác DEF lên mặt phẳng đáy qua phép chiếu song song theo phương SC;

D. Tam giác CKN là ảnh của tam giác DEF lên mặt phẳng đáy qua phép chiếu song song theo phương SB.

Xem đáp án

Đáp án đúng là: B

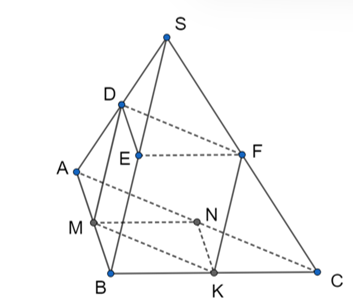
Cho hình tứ diện có D, E, F, M, N, K lần lượt là trung điểm của các cạnh SA, SB, SC, AB, AC, BC (Như hình vẽ). (ảnh 2)

Ta dễ dàng nhận thấy: MD và KF là các đường trung bình của các tam giác SAB và SBC.

Do đó: MD // SB, KF // SB; M và K Î (ABC).

ÞM, K là ảnh của D, F lên (ABC) qua phép chiếu song song theo phương SB.

E Î SB, SB Ç (ABC) = B Þ B là ảnh của E lên (ABC) qua phép chiếu song song theo phương SB.

Từ chứng minh trên ta kết luận đáp án đúng là C.

Câu 2:

Cho hình nón đỉnh S, đáy là đường tròn tâm O đường kính AB = 4. D, E lần lượt là trung điểm của SA và SB. Vẽ đường tròn tâm O¢ đường kính DE. Biết SO vuông góc với mặt phẳng đáy. Ảnh của đường tròn (O¢) lên mặt phẳng đáy qua phép chiếu song song theo phương SO có bán kính dài bao nhiêu?

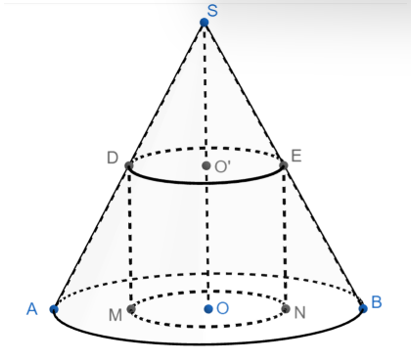
Cho hình nón đỉnh S, đáy là đường tròn tâm O đường kính AB = 4. D, E lần lượt là trung điểm của SA và SB (ảnh 1)

A. 2;

B. 4;

C. 3;

D. 1.

Xem đáp án

Đáp án đúng là: D

Do O¢ Î SO, SO cắt mặt phẳng đáy tại O;

Þ O là ảnh của O¢ lên mặt phẳng đáy qua phép chiếu song song theo phương SO.

Lần lượt kẻ các đường song song với SO, đi qua D và E, cắt đáy lần lượt tại M và N.

Do đó, ảnh của (O¢) lên mặt phẳng đáy qua phép chiếu song song theo phương SO là (O) đường kính MN.

Nhận thấy DO¢OM là một hình chữ nhật Þ DO¢ = MO;

Mà DO¢ = $\frac{1}{2}$ AO (DO¢ là đường trung bình của tam giác SAO);

Û DO¢ = $\frac{1}{2}$ . $\frac{1}{2}$ .AB = 1.

Þ MO = DO¢ = 1.

Câu 3:

Cho hình lăng trụ ABC.A¢B¢C¢, M là trung điểm của AC. Thực hiện phép chiếu song song lên mặt phẳng chiếu (A¢B¢C¢) theo phương CC’ biến M thành M’. Chọn mệnh đề đúng?

A. M¢ là trung điểm của A¢B¢;

B. M¢ là trung điểm của B¢C¢;

C. M¢ là trung điểm của A¢C¢;

D. Cả ba đáp án trên đều sai.

Xem đáp án

Đáp án đúng là: C

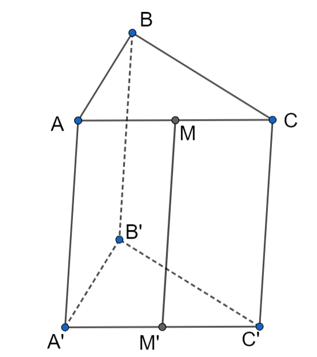
Cho hình lăng trụ ABC.A¢B¢C¢, M là trung điểm của AC. Thực hiện phép chiếu song song lên mặt phẳng chiếu (A¢B¢C¢) (ảnh 1)

Từ M kẻ đường thẳng song song với CC¢, cắt mặt phẳng đáy tại M¢.

Nhận thấy M là trung điểm của AC nên MM¢ là đường trung bình của tứ giác ACC¢A¢.

Suy ra M¢ là trung điểm của A¢C¢.

Câu 4:

Cho mặt phẳng (α), tam giác ABC nằm trên mặt phẳng (a); phương chiếu d. Biết hình chiếu (theo phương d) của tam giác ABC lên mặt phẳng (P) là một đoạn thẳng. Khẳng định nào sau đây đúng?

A. (P) // (α);

B. (P) ≡ (α);

C. d Ì (α) hoặc (α) // d;

D. Không có đáp án đúng.

Xem đáp án

Đáp án đúng là: C

Cho mặt phẳng (α), tam giác ABC nằm trên mặt phẳng (a); phương chiếu d. Biết hình chiếu (theo phương d) của tam giác ABC (ảnh 1)

Hình chiếu của tam giác ABC trên (P) là một đoạn thẳng, suy ra các đường thẳng đi qua A, B, C và song song với phương chiếu d là đồng phẳng.

Điều này xảy ra khi d nằm trên (a) hoặc d // (a).

Câu 5:

Có hình lăng trụ ABC.A¢B¢C¢; AB, A¢B¢ có trung điểm lần lượt là I và I¢. Qua phép chiếu song song lên mặt phẳng chiếu (CBB¢C¢) theo phương chiếu AI biến I¢ thành điểm nào sau đây?

A. A¢;

B. B¢;

C. C¢;

D. I.

Xem đáp án

Đáp án đúng là: B

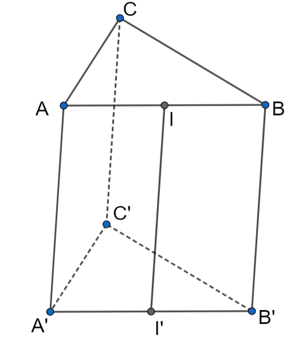
Có hình lăng trụ ABC.A¢B¢C¢; AB, A¢B¢ có trung điểm lần lượt là I và I¢. Qua phép chiếu song song lên mặt phẳng chiếu (CBB¢C¢) (ảnh 1)

Nhận thấy: I¢B¢ // AI, I¢B¢ Ç CBB¢C¢ = B¢.

Suy ra B¢ là ảnh của I¢ lên CBB¢C¢ qua phép chiếu song song theo phương AI.

Câu 6:

Thực hiện phép chiếu song song lên mặt phẳng (P), hai đường thẳng d₁ và d₂ có hình chiếu là hai đường thẳng song song a và b. Khi đó

A. d₁ và d₂ phải song song với nhau;

B. d₁ và d₂ phải cắt nhau;

C. d₁ và d₂ có thể chéo nhau hoặc song song với nhau;

D. d₁ và d₂ không thể song song.

Xem đáp án

Đáp án đúng là: C

Nếu a // b, suy ra mặt phẳng (a, d₁) song song mặt phẳng (b, d₂).

Khi đó a và b có thể song song hoặc chéo nhau.

Câu 7:

Thực hiện phép chiếu song song lên mặt phẳng (Q), hai đường thẳng chéo nhau d₁ và d₂ có hình chiếu là 2 đường thẳng a và b. Mệnh đề nào sau đây đúng?

A. d₁ và d₂ luôn cắt nhau;

B. d₁ và d₂có thể trùng nhau;

C. d₁ và d₂không thể song song;

D. d₁ và d₂có thể cắt nhau hoặc song song với nhau.

Xem đáp án

Đáp án đúng là: D

Gọi D là phương chiếu; d₁, a Ì (a₁), d₂, b Ì (a₂) Þ D // (a₁), D // (a₂).

+ Nếu (a₁) Ç (a₂) thì a và b cắt nhau.

+ Nếu (a₁) // (a₂) thì a // b.

Câu 8:

Cho tứ diện ABCD. Giả sử N là trung điểm của AB. trên mặt phẳng (BCD), hình chiếu của N qua phép chiếu song song theo phương AC là

A. Trung điểm BD;

B. Trung điểm BC;

C. Trọng tâm giác BCD;

D. Điểm B.

Xem đáp án

Đáp án đúng là: B

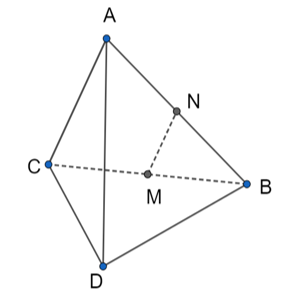
Cho tứ diện ABCD. Giả sử N là trung điểm của AB. trên mặt phẳng (BCD), hình chiếu của N (ảnh 1)

Từ N kẻ đường thẳng d song song với AC.

Do N là trung điểm của AB nên d đi qua trung điểm của BC.

Gọi M = d Ç BC Þ M là ảnh của N trên (BCD) qua phép chiếu song song theo phương AC.

Câu 9:

Cho hình chóp S.ABCD có SA = SB = a, ∆SAC và ∆SBD vuông cân tại A và B, đáy ABCD là tứ giác đều. d là đường thẳng vuông góc với (ABCD). Hình chiếu của S lên mặt phẳng đáy theo phương d là là S¢. Hỏi độ dài của S¢C là?

A. 2a

B. $\frac{3 a}{2}$

C. $\frac{a \sqrt{5}}{2}$

D. $\frac{5 a}{2}$

Xem đáp án

Đáp án đúng là: C

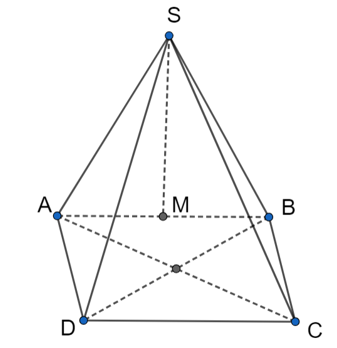
Cho hình chóp S.ABCD có SA = SB = a, ∆SAC và ∆SBD vuông cân tại A và B, đáy ABCD là tứ giác đều. d là đường thẳng vuông góc với (ABCD) (ảnh 1)

Theo giả thiết: AD ^ SA, AD ^ AB nên AD ^ (SAB) (1)

Mà SA = SB nên ∆SAB cân tại S nên trung tuyến SM của ∆SAB vuông góc với AB (2)

Từ (1) và (2) suy ra SM ^ (ABCD).

Suy ra S¢ º M.

Có S¢C = MC = $\sqrt{B M^{2} + B C^{2}} = \sqrt{{(\frac{a}{2})}^{2} + a^{2}} = a \frac{\sqrt{5}}{2}$

.

Câu 10:

Cho nửa hình trụ có các đáy là nửa đường tròn tâm O, đường kính AB; nửa đường tròn tâm O¢, đường kính CD. M Î (O) sao cho MA = MB, N Î (O¢) sao cho NC = ND. Phép chiếu song song lên mặt phẳng (ABCD) theo phương MO¢ biến ∆CDN thành tam giác có diện tích là bao nhiêu, biết ABCD là hình vuông cạnh a.

A. $\frac{a^{2}}{2}$

B. $\frac{3 a^{2}}{2}$

C. $\frac{a^{2} \sqrt{3}}{2}$

D. $\frac{5 a^{2}}{2}$

Xem đáp án

Đáp án đúng là: A

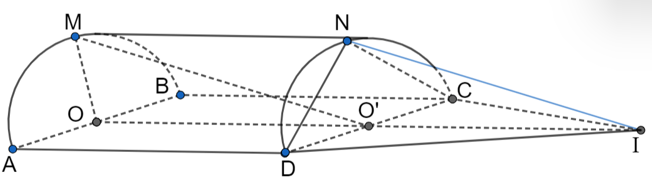
Cho nửa hình trụ có các đáy là nửa đường tròn tâm O, đường kính AB; nửa đường tròn tâm O¢, đường kính CD. M Î (O) (ảnh 1)

Gọi I là hình chiếu của N theo phép chiếu song song đã cho.

Þ Phép chiếu biến ∆CDN thành ∆CDI.

Ta nhận thấy MO, NO¢ ^ (ABCD) Þ MO // NO¢ và MO = NO¢.

Þ MNO¢O là hình bình hành suy ra MN // OO¢.

Dễ thấy MNIO¢ là hình bình hành Þ MN // O¢I và MN = O¢I.

Þ O¢ là trung điểm của OI.

S_CDI = $\frac{1}{2}$ .O¢I.CD = $\frac{1}{2}$ .a.a = $\frac{a^{2}}{2}$ .