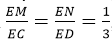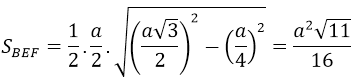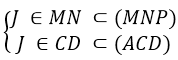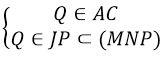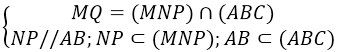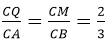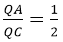Trắc nghiệm Đề kiểm tra Chương 2 Hình học 11 có đáp án
-
1012 lượt thi
-
20 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 2:
Trong các mệnh đề sau, những mệnh đề nào đúng?
(1) Hai đường thẳng chéo nhau thì không có điểm chung.
(2) Hai đường thẳng không có điểm chung thì chéo nhau.
(3) Hai đường thẳng chéo nhau thì không cùng thuộc một mặt phẳng.
(4) Hai đường thẳng không song song thì chéo nhau.
 Xem đáp án
Xem đáp án
Đáp án D
Câu 3:
Cho hai đường thẳng a và b phân biệt cùng song song với mặt phẳng (P). mệnh đề nào đúng trong các mệnh đề sau?
 Xem đáp án
Xem đáp án
Đáp án D
Câu 4:
Cho một mặt phẳng (P) và hai đường thẳng song song a, b. Mệnh đề nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án A
Câu 5:
Cho đường thẳng a song song với mặt phẳng (P). Khi đó, số đường thẳng phân biệt nằm trong (P) và song song với a có thể là:
 Xem đáp án
Xem đáp án
Đáp án D
Câu 6:
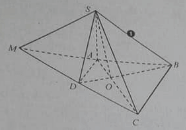
Cho hình chóp S.ABCD với AC và BD cắt nhau tại M, AB và CD cắt nhau tại N. Hai mặt phẳng (SAC), (SBD) có giao tuyến là:
 Xem đáp án
Xem đáp án
Đáp án A
Câu 8:
Cho hình chóp S.ABCD có các cạnh AB và CD không song song ; O là giao điểm của hai đường thẳng AC và BD. Giao tuyến của các cặp mặt phẳng (SAC) và (SBD), (SAB) và (SCD) lần lượt là:
 Xem đáp án
Xem đáp án
Đáp án B
Câu 9:
Cho hình chóp S.ABCD với ABCD là hình thang đáy nhỏ AD. Khi đó giao tuyến của hai mặt phẳng (SAB) và (SCD) là:
 Xem đáp án
Xem đáp án
Trong mặt phẳng (ABCD), AB cắt CD tại M, suy ra M là điểm chung của hai mặt phẳng (SAB) và (SCD). Lại có S là điểm chung thứ hai. Vậy giao tuyến của hai mặt phẳng nói trên là đường thẳng SM.
Đáp án D
Câu 10:
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC, AD và G là trọng tâm của tam giác BCD. Giao tuyến của hai mặt phẳng (BMN) và (GCD) là:
 Xem đáp án
Xem đáp án
Đáp án B
Câu 11:
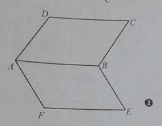
Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt. kết luận nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Phương án A sai vì AD và (BEF) cắt nhau tại A.
Phương án B đúng vì AD // BC, AF // BE
Phương án C sai vì (ABD) và (EFC) có điểm C chung
Đáp án B
Câu 12:
Cho tứ diện ABCD, điểm M thuộc cạnh AC, điểm N thuộc cạnh CD. Mặt phẳng (∝) đi qua MN, song song với AB. Tìm thiết diện của (∝) với tứ diện ABCD.
 Xem đáp án
Xem đáp án
Đáp án A
Câu 13:
Cho tứ diện ABCD, M, N lần lượt là trọng tâm tam giác ABC, ABD. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Gọi E là trung điểm của AB. M, N lần lượt là trọng tâm các tam giác ABC, ABD nên:
Theo định lí Ta – lét ta có MN // CD.
Đáp án A
Câu 14:
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành . gọi I, J lần lượt là trung điểm của SB và SD. Thiết diện của mặt phẳng (AIJ) với hình chóp là:
 Xem đáp án
Xem đáp án
Đáp án B
Câu 15:
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Điểm M thuộc đoạn thẳng SB. Tìm giao tuyến của mặt phẳng (ADM) với (SBC).
 Xem đáp án
Xem đáp án
Do AD // BC, M thuộc (SBC) nên giao tuyến của (ADM) với (SBC) là đường thẳng qua M và song song với BC.
Đáp án B
Câu 16:
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và CB. M là điểm thuộc cạnh SD. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Trong mặt phẳng (ABCD) ta có AC cắt BD tại O, IJ cắt BD tại E. trong mặt phẳng (SBD), ME cắt SO tại G. Ta có G thuộc (MIJ). (MIJ) chứa IJ // AC nên giao tuyến của (MIJ) với (SAC) là đường thẳng qua G và song song với AC.
Đáp án D
Câu 17:
Cho hình chóp S.ABCD đáy là hình bình hành. K là trung điểm của SA, H là điểm thuộc cạnh AC và không phải là trung điểm của AC. Mặt phẳng (∝) chứa KH và song song với BD. Thiết diện của hình chóp S.ABCD với (∝) là hình gì?
 Xem đáp án
Xem đáp án
Đáp án D
Câu 18:
Cho tứ diện đều ABCD cạnh a. gọi M là trung điểm của AB, qua M dựng mặt phẳng (P) song song với mặt phẳng (BCD). Tìm diện tích thiết diện của (P) và tứ diện.
 Xem đáp án
Xem đáp án
Đáp án A
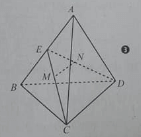
Câu 19:
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trọng tâm của ∆ABC và ∆ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BMN) là:
 Xem đáp án
Xem đáp án
Trong (ABD), BN cắt AD tại F. Trong (ABC), BM cắt AC tại E.
Do M, N lần lượt là trọng tâm của ∆ABC và ∆ABD nên E, F lần lượt là trung điểm của AC, AD
Tứ diện ABCD có cạnh bằng a nên BE = BF = (a√3)/2
Thiết diện là tam giác cân BEF tại B, có đay EF = a/2
Diện tích BEF là
Đáp án D
Câu 20:
Cho tứ diện ABCD, M là điểm thuộc BC sao cho MC = 2MB. N, P lần lượt là trung điểm của BD và AD. Điểm Q là giao điểm của AC với (MNP). Tính QA/QC.
 Xem đáp án
Xem đáp án
NP là đường trung bình của ∆ACD ⇒ NP // AB, mà AB ⊂ (ABC) ⇒NP // (ABC)
P ∈ (MNP) ∩ (ACD) (1)
Trong mặt phẳng (BCD) gọi J = MN ∩ CD, có
J ∈ (MNP) ∩ (ACD) (2)
Từ (1) và (2) : (MNP) ∩ (ACD) = JP
Trong mặt phẳng (ACD) gọi Q = JP ∩ AC. Có:
⇒ Q = AC ∩ (MNP). Có:
⇒MQ // NP // AB
Theo định lí Ta – lét có
Kết luận:
Đáp án A