19 câu hỏi trắc nghiệm thuộc Dạng 2: Chứng minh hai mặt phẳng vuông góc, chứng minh đường thẳng vuông góc với mặt phẳng và các bài toán liên quan có đáp án

Câu 1:

A B ⊥ (B C D)

. Trong

Δ B C D

vẽ các đường cao BE và DF cắt nhau ở O. Trong (ADC) vẽ

D K ⊥ A C

tại K. Khẳng định nào sau đây sai ?

A. $(A D C) ⊥ (A B E)$

B. $(A D C) ⊥ (D F K)$

C. $(A D C) ⊥ (A B C)$

D. $(B D C) ⊥ (A B E)$

Xem đáp án

Chọn C

Cho tứ diện ABCD có . Trong AB vuông góc mp BCD vẽ các đường cao BE và DF cắt nhau ở O. Trong (ADC) vẽ DK vuông góc mp AC tại K. (ảnh 1)

* Ta có $\begin{array}{l} C D ⊥ B E \\ C D ⊥ A B \end{array}\} \Rightarrow \begin{matrix} \begin{array}{l} C D ⊥ (A B E) \\ C D \subset (A D C) \end{array}\} \Rightarrow (A D C) ⊥ (A B E) \end{matrix}$ .

Vậy “ $(A D C) ⊥ (A B E)$ ”: ĐÚNG.

* $\begin{array}{l} D F ⊥ B C \\ D F ⊥ A B \end{array}\} \Rightarrow \begin{array}{l} D F ⊥ (A B C) \\ S C \subset (A B C) \end{array}\} \Rightarrow \begin{array}{l} D F ⊥ A C \\ D K ⊥ A C \end{array}\} \Rightarrow \begin{array}{l} A C ⊥ (D F K) \\ A C \subset (A D C) \end{array}\} \Rightarrow (A D C) ⊥ (D F K)$

Vậy “ $(A D C) ⊥ (D F K)$ ”: ĐÚNG.

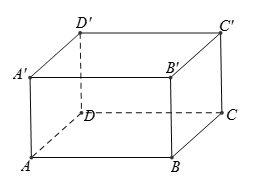
* Ta có $\begin{array}{l} C D ⊥ B E \\ C D ⊥ A B \end{array}\} \Rightarrow \begin{matrix} \begin{array}{l} C D ⊥ (A B E) \\ C D \subset (B D C) \end{array}\} \Rightarrow (B D C) ⊥ (A B E) \end{matrix}$

Vậy “ $(B D C) ⊥ (A B E)$ ”: ĐÚNG.

* “ $(A D C) ⊥ (A B C)$ ”: SAI

Câu 2:

Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chọn khẳng định sai trong các khẳng định sau?

A. $(A B E) ⊥ (A D C)$

B. $(A B D) ⊥ (A D C)$

C. $(A B C) ⊥ (D F K)$

D. $(D F K) ⊥ (A D C)$

Xem đáp án

Chọn B

Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). Gọi BE và DF là hai đường cao của tam giác BCD, (ảnh 1)

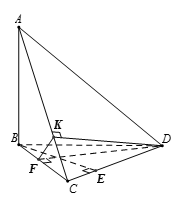
Ta có:

$\{\begin{cases} (A B C) ⊥ (B C D) \\ (A B D) ⊥ (B C D) \\ (A B C) \cap (A B D) = A B \end{cases} \Rightarrow A B ⊥ (B C D)$

Mặt khác: $\{\begin{cases} C D ⊥ B E \\ C D ⊥ A B \end{cases} \Rightarrow C D ⊥ (A B E)$ nên câu A đúng.

$\{\begin{cases} (A B C) ⊥ (B C D) \\ (A B C) \cap (B C D) = B C \\ D F ⊥ B C \end{cases} \Rightarrow D F ⊥ (A B C)$ nên câu C đúng.

Theo trên ta có $D F ⊥ (A B C)$ nên $D F ⊥ A C$

Vậy ta có $\{\begin{cases} A C ⊥ D F \\ A C ⊥ D K \end{cases} \Rightarrow A C ⊥ (D K F) \Rightarrow (A C D) ⊥ (D K F)$ . Do đó câu D đúng.

Câu 3:

Cho hình hộp chữ nhật ABCD.A'B'C'D'. Khẳng định nào sau đây không đúng?

A. Tồn tại điểm O cách đều tám đỉnh của hình hộp.

B. Hình hộp có 6 mặt là 6 hình chữ nhật.

C. Hai mặt ACC'A' và BDD'B' vuông góc nhau.

D. Hình hộp có 4 đường chéo bằng nhau và đồng qui tại trung điểm của mỗi đường.

Xem đáp án

Chọn C

Cho hình hộp chữ nhật ABCD.A'B'C'D'. Khẳng định nào sau đây không đúng? (ảnh 1)

Câu 4:

Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC) vuông góc với đáy (ABC). Khẳng định nào sau đây sai ?

A. Đáy là đa giác đều.

B. Các mặt bên là những hình chữ nhật nằm trong mặt phẳng vuông góc với đáy.

C. Các cạnh bên là những đường cao.

D. Các mặt bên là những hình bình hành.

Xem đáp án

Chọn D

Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC) vuông góc với đáy (ABC). Khẳng định nào sau đây sai ? (ảnh 1)

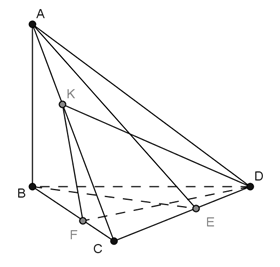
Ta có: $\{\begin{cases} (S B C) ⊥ (A B C) \\ (S A C) ⊥ (A B C) \\ S C = (S B C) \cap (S A C) \end{cases} \Rightarrow S C ⊥ (A B C)$ . Do đó câu A và B đúng

C. Sai. vì nếu $A' \in S B$ thì hai mặt phẳng (SAB) và (SBC) phải vuông góc với nhau theo giao tuyến SB

D. Ta có: $\{\begin{cases} S C ⊥ (A B C) \\ S C \subset (S A C) \end{cases} \Rightarrow (S A C) ⊥ (A B C)$ theo giao tuyến AC

Mà BK là đường cao của $Δ A B C \Rightarrow B K ⊥ A C \Rightarrow B K ⊥ (S A C)$ . Vậy D đúng

Câu 5:

Cho hình lăng trụ ABCD.A'B'C'D'. Hình chiếu vuông góc của A' lên (ABC) trùng với trực tâm H của tam giác ABC. Khẳng định nào sau đây không đúng?

A. $B B ’ C ’ C$ là hình chữ nhật

B. $(A A ’ H) ⊥ (A ’ B ’ C ’)$

C. $(B B ’ C ’ C) ⊥ (A A ’ H)$

D. $(A A ’ B ’ B) ⊥ (B B ’ C ’ C)$

Xem đáp án

Chọn D

Cho hình lăng trụ ABCD.A'B'C'D'. Hình chiếu vuông góc của A' lên ABC trùng với trực tâm H của tam giác ABC. (ảnh 1)

Ta có $B C ⊥ (A ’ A H)$ nên $B C ⊥ B B ’$ , nếu $(A A ’ B ’ B) ⊥ (B B ’ C ’ C)$ thì $B C ⊥ A B$ vô lý vì H trùng A.

Câu 6:

Cho hình chóp S.ABC có

S A ⊥ (A B C)

và đáy ABC là tam giác cân ở A. Gọi H là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây đúng?

A.

H \in S B

B. H trùng với trọng tâm tam giác SBC .

C.

H \in S C

D.

H \in S I

( I là trung điểm của BC ).

Xem đáp án

Chọn D

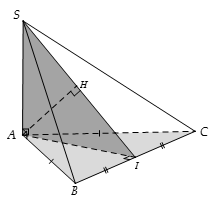
Cho hình chóp S.ABC có SA vuông góc mp ABC và đáy ABC là tam giác cân ở A. Gọi H là hình chiếu vuông góc của A lên (SBC). (ảnh 1)

Gọi I là trung điểm của BC $\Rightarrow A I ⊥ B C$ mà $B C ⊥ S A \Rightarrow B C ⊥ (S A I)$

Khi đó H là hình chiếu vuông góc của A lên (SBC). Suy ra

H \in S I

Câu 7:

Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC) vuông góc với đáy (ABC). Khẳng định nào sau đây sai?

A.

S C ⊥ (A B C)

B. Nếu A' là hình chiếu vuông góc của A lên (SBC) thì

A^{'} \in S B

C.

(S A C) ⊥ (A B C)

D. BK là đường cao của tam giác ABC thì

B K ⊥ (S A C)

Xem đáp án

Chọn B

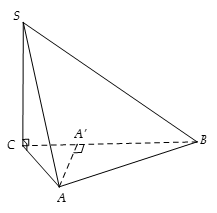
Ta có:

$\{\begin{matrix} (S A C) \cap (S B C) = S C \\ (S A C) ⊥ (A B C) \\ (S B C) ⊥ (A B C) \end{matrix} \Rightarrow S C ⊥ (A B C)$

Gọi A' là hình chiếu vuông góc của A lên (SBC), khi đó $A A^{'} ⊥ (S B C) \Rightarrow A A^{'} ⊥ B C \Rightarrow A^{'} \in B C$

Suy ra đáp án B sai

Câu 8:

Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với đáy (ABC), tam giác ABC vuông cân ở A và có đường cao AH,

(H \in B C)

. Gọi O là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây đúng?

A.

S C ⊥ (A B C)

B.

(S A H) ⊥ (S B C)

C.

O \in S C

D. Góc giữa (SBC) và (ABC) là góc

\hat{S B A}

Xem đáp án

Chọn B

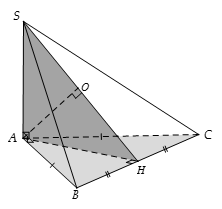
Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với đáy (ABC), tam giác ABC vuông cân ở A và có đường cao AH, H thuộc BC (ảnh 1)

Ta có:

$\{\begin{matrix} (S A B) \cap (S A C) = S A \\ (S A C) ⊥ (A B C) \\ (S A B) ⊥ (A B C) \end{matrix} \Rightarrow S A ⊥ (A B C)$

Gọi H là trung điểm của BC

$\Rightarrow A H ⊥ B C$

mà $B C ⊥ S A \Rightarrow B C ⊥ (S A H) \Rightarrow (S B C) ⊥ (S A H)$

Khi đó O là hình chiếu vuông góc của A lên (SBC)

Thì suy ra $O \in S I$ và $\hat{((S B C), (A B C))} = \hat{S H A}$

Vậy đáp án B đúng.

Câu 9:

Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân ở A. H là trung điểm BC. Khẳng định nào sau đây sai ?

A. Các mặt bên của ABC.A'B'C' là các hình chữ nhật bằng nhau.

B. (AA'H) là mặt phẳng trung trực của BC

C. Nếu O là hình chiếu vuông góc của A lên (A'BC) thì

O \in A^{'} H

D. Hai mặt phẳng (AA'B'B) và (AA'C'C) vuông góc nhau.

Xem đáp án

Chọn A

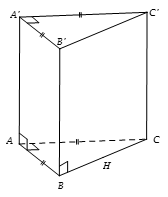
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân ở A. H là trung điểm BC. Khẳng định nào sau đây sai ? (ảnh 1)

Vì ABC là tam giác vuông cân ở A

$\Rightarrow A B = A C \neq B C$

nên các mặt bên của lăng trụ không bằng nhau.

Vậy đáp án A sai.

Câu 10:

Cho hình hộp chữ nhật ABCD.A'B'C'D'. Khẳng định nào sau đây không đúng?

A. Hình hộp có 6 mặt là 6 hình chữ nhật.

B. Hai mặt (ACC'A') và (BDD'B') vuông góc nhau.

C. Tồn tại điểm O cách đều tám đỉnh của hình hộp.

D. Hình hộp có đường chéo bằng nhau và đồng qui tại trung điểm của mỗi đường.

Xem đáp án

Chọn B

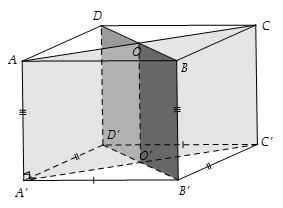
Ta có: ABCD là hình chữ nhật nên AC không vuông góc với BD

Suy ra hai mặt (ACC'A') và (BDD'B') không vuông góc với nhau.

Vậy đáp án B sai

Câu 11:

Cho hình lập phương

A B C D . A_{1} B_{1} C_{1} D_{1}

. Mặt phẳng

(A_{1} B D)

không vuông góc với mặt phẳng nào dưới đây?

A. $(A B_{1} D)$

B. $(A C C_{1} A_{1})$

C. $(A B D_{1})$

D. $(A_{1} B C_{1})$

Xem đáp án

Chọn D

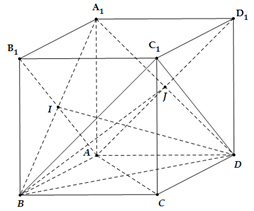
Cho hình lập phương ABCD.A1B1C1. Mặt phẳng (A1BD) không vuông góc với mặt phẳng nào dưới đây? (ảnh 1)

* Gọi $I = A B_{1} \cap A_{1} B$

Tam giác $A_{1} B D$ đều có là đường trung tuyến nên $D I ⊥ A_{1} B$

$D A ⊥ (A A_{1} B_{1} B) \Rightarrow D A ⊥ A_{1} B$

\begin{array}{l} A_{1} B ⊥ D I \\ A_{1} B ⊥ A D \end{array}\} \Rightarrow A_{1} B ⊥ (A B_{1} D)

nên A đúng.

* Ta có $\begin{array}{l} B D ⊥ A C \\ B D ⊥ A A_{1} \end{array}\} \Rightarrow B D ⊥ (A C C_{1} A_{1}) \Rightarrow (A_{1} B D) ⊥ (A C C_{1} A_{1})$ nên B đúng.

* Gọi $J = A D_{1} \cap A_{1} D$

Tam giác $A_{1} B D$ đều có BJ là đường trung tuyến nên $B J ⊥ A_{1} D$

$B A ⊥ (A A_{1} D_{1} D) \Rightarrow B A ⊥ A_{1} D$

$\begin{array}{l} A_{1} D ⊥ B J \\ A_{1} D ⊥ B A \end{array}\} \Rightarrow A_{1} B ⊥ (A B D_{1})$ nên C đúng. Chọn D.

Câu 12:

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khẳng định nào sau đây sai?

A. Tam giác AB'C là tam giác đều.

B. Nếu

α

là góc giữa AC' và (ABCD) thì

\cos α = \sqrt{\frac{2}{3}}

C. ACC'A' là hình chữ nhật có diện tích bằng

2 a^{2}

D. Hai mặt (AA'C'A) và (BB'D'D) ở trong hai mặt phẳng vuông góc với nhau.

Xem đáp án

Chọn C

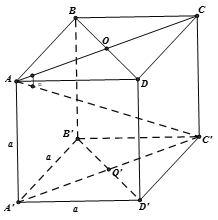
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khẳng định nào sau đây sai? (ảnh 1)

+ Cách 1: Chứng minh trực tiếp chỉ ra C là đáp án sai.

Từ giả thiết dễ dàng tính được $A C = a \sqrt{2}$

Mặt khác vì ABCD.A'B'C'D' là hình lập phương nên suy ra $\hat{A A^{'} C^{'}} = 90 °$

Xét tứ giác ACC'A' có $\{\begin{cases} A A^{'} / / C C^{'} \\ A A^{'} = C C^{'} = a \\ \hat{A A^{'} C^{'}} = 90 ° \end{cases}$ => ACC'A' là hình chữ nhật có các cạnh a và $a \sqrt{2}$

Diện tích hình chữ nhật ACC'A' là : $S = a . a \sqrt{2} = a^{2} \sqrt{2}$ (đvdt)

=> đáp án C sai.

+ Cách 2: Chứng minh 3 đáp án A, B, D đều đúng và suy ra đáp án C sai.

Câu 13:

Cho hình chóp S.ABC có đường cao SH. Xét các mệnh đề sau:

(I) SA = SB = SC

(II) H trùng với tâm đường tròn ngoại tiếp tam giác ABC

(III) Tam giác ABC là tam giác đều.

(IV) H là trực tâm tam giác ABC

Các yếu tố nào chưa đủ để kết luận S.ABC là hình chóp đều?

A. (I) và (II)

B. (II) và (III)

C. (III) và (IV)

D. (IV) và (I)

Xem đáp án

Chọn A

Câu 14:

Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Khẳng định nào sau đây sai?

A. Hai mặt ACC'A' và BDD'B' vuông góc nhau.

B. Bốn đường chéo AC', A'C, BD', B'D bằng nhau và bằng

a \sqrt{3}

C. Hai mặt ACC'A' và BDD'B' là hai hình vuông bằng nhau.

D. $A C ⊥ B D^{'}$

Xem đáp án

Chọn C

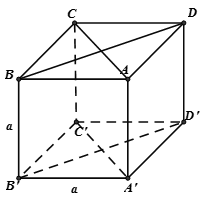
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Khẳng định nào sau đây sai? (ảnh 1)

Vì theo giả thiết ABCD.A'B'C'D' ta dễ dàng chỉ ra được:

+ $\{\begin{cases} A C ⊥ B D \\ A C ⊥ B B^{'} \end{cases}$ và BD cắt BB' cùng nằm trong $(B B^{'} D^{'} D) \Rightarrow A C ⊥ (B B^{'} D^{'} D)$

Mà $B D^{'} \subset (B B^{'} D^{'} D) \Rightarrow \Rightarrow A C ⊥ B D^{'} \Rightarrow$ đáp án D đúng.

+ $\{\begin{cases} A C \subset (A C C^{'} A^{'}) \\ A C ⊥ (B B^{'} D^{'} D) \end{cases} \Rightarrow (A C C^{'} A^{'}) ⊥ (B B^{'} D^{'} D)$ => đáp án A đúng.

+ Áp dụng đình lý Pytago trong tam giác B'A'D' vuông tại A' ta có:

$B^{'} {D^{'}}^{2} = B^{'} {A^{'}}^{2} + A^{'} {D^{'}}^{2} = a^{2} + a^{2} = 2 a^{2}$

Áp dụng định lý Pytago trong tam giác BB'D' vuông tại B' ta có: $B {D^{'}}^{2} = B {B^{'}}^{2} + B^{'} {D^{'}}^{2} = a^{2} + 2 a^{2} = 3 a^{2}$

Hoàn toàn tương tự ta tính được độ dài các đường chéo còn lại của hình lập phương đều bằng nhau và bằng $a \sqrt{3}$ => đáp án B đúng.

+ Xét tứ giác ACC'A' có $\{\begin{cases} A C / / A^{'} C^{'} \\ A C = A^{'} C^{'} = a \sqrt{3} \\ A A^{'} = C C^{'} = a \\ \hat{A C C^{'}} = 90 ° \end{cases} \Rightarrow A C C^{'} A^{'}$ là hình chữ nhật. hoàn toàn tương tự ta cũng chỉ ra BDD'B' cũng là hình chữ nhật có các cạnh là a và $a \sqrt{3}$

=> Hai mặt ACC'A' và BDD'B' là hai hình vuông bằng nhau => đáp án C sai.

Câu 15:

Cho hình lăng trụ ABCD.A'B'C'D'. Hình chiếu vuông góc của A' lên (ABC) trùng với trực tâm H của tam giác ABC. Khẳng định nào sau đây không đúng?

A. $(A A^{'} B^{'} B) ⊥ (B B^{'} C^{'} C)$

B. $(A A^{'} H) ⊥ (A^{'} B^{'} C^{'})$

C. BB'C'C là hình chữ nhật

D. $(B B^{'} C^{'} C) ⊥ (A A^{'} H)$

Xem đáp án

Chọn A

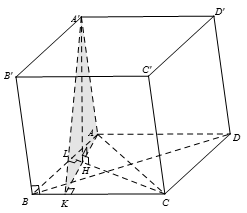
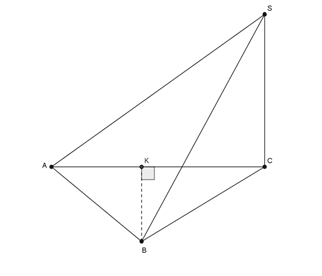
Gọi K là hình chiếu vuông góc của A lên BC

$\Rightarrow H \in A K, B C ⊥ A K, B C ⊥ A^{'} H \Rightarrow B C ⊥ (A A^{'} H)$

\Rightarrow \{\begin{matrix} (A A^{'} H) ⊥ (A^{'} B^{'} C^{'}) \\ (B B^{'} C^{'} C) ⊥ (A A^{'} H) \\ B C ⊥ B B^{'} \end{matrix}

nên đáp án B,C,D đúng

Câu 16:

Hình hộp ABCD.A'B'C'D' trở thành hình lăng trụ tứ giác đều khi phải thêm các điều kiện nào sau đây?

A. Tất cả các cạnh đáy bằng nhau và cạnh bên vuông góc với mặt đáy.

B. Cạnh bên bằng cạnh đáy và cạnh bên vuông góc với mặt đáy.

C. Có một mặt bên vuông góc với mặt đáy và đáy là hình vuông.

D. Các mặt bên là hình chữ nhật và mặt đáy là hình vuông.

Xem đáp án

Chọn D.

Theo lí thuyết lăng trụ tứ giác đều là lăng trụ đứng có đáy là hình vuông.

Câu 17:

Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng a , góc giữa hai mặt phẳng (ABCD) và (ABC') có số đo bằng 60^o. Cạnh bên của hình lăng trụ bằng:

A. 3a

B. $a \sqrt{3}$

C. 2a

D. $a \sqrt{2}$

Xem đáp án

Chọn B

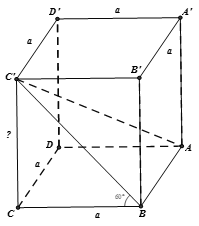
Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng a , góc giữa hai mặt phẳng (ABCD) và (ABC') có số đo (ảnh 1)

Ta có: $(A B C D) \cap (A B C^{'}) = A B$

Từ giả thiết ta dễ dàng chứng minh được: $A B ⊥ (B B^{'} C^{'} C)$ mà $C^{'} B \subset (B B^{'} C^{'} C) \Rightarrow A B ⊥ C^{'} B$

Mặt khác: $C B ⊥ A B$

$\Rightarrow ((A B C D), (A B C^{'})) = (C B, C^{'} B) = \hat{C B C^{'}} = 60 °$

Áp dụng hệ thức lượng trong tam giác BCC' vuông tại C ta có:

$\tan \hat{C B C^{'}} = \frac{C C^{'}}{C B} \Rightarrow C C^{'} = C B . \tan \hat{C B C^{'}} = a . \tan 60 ° = a \sqrt{3}$

Câu 18:

Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến

Δ

. Lấy A, B cùng thuộc

Δ

và lấy C trên (P), D trên (Q) sao cho

A C ⊥ A B

,

B D ⊥ A B

và AB = AC = BD. Thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng

(α)

đi qua A và vuông góc với CD là hình gì?

A. Tam giác cân.

B. Hình vuông.

C. Tam giác đều.

D. Tam giác vuông.

Xem đáp án

Chọn D

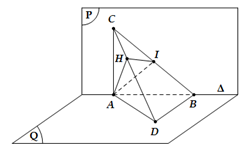
Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến denta. Lấy A, B cùng thuộc denta và lấy C trên (P), D trên (Q) sao cho AC vuông góc AB, BD vuông góc và AB = AC = BD. (ảnh 1)

Gọi I là trung điểm của BC. Vì tam giác ABC vuông cân tại A nên $A I ⊥ B C$

Ta có:

$\begin{array}{l} (P) ⊥ (Q) \\ (P) \cap (Q) = d \\ (Q) \supset B D ⊥ d \end{array}\} \Rightarrow B D ⊥ (P) \Rightarrow B D ⊥ A I \begin{array}{l} A I ⊥ B C \\ A I ⊥ B D \end{array}\} \Rightarrow A I ⊥ (B C D) \Rightarrow A I ⊥ C D$

Trong (ACD), dựng đường thẳng đi qua A và vuông góc với CD cắt CD tại H

Thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng $(α)$ là tam giác AHI

Vì

A I ⊥ (B C D) \Rightarrow A I ⊥ H I

nên tam giác AHI là tam giác vuông tại I

Câu 19:

Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a, CD = 2x. với giá trị nào của x thì hai mặt phẳng (ABC) và (ABD) vuông góc.

A. $\frac{a \sqrt{3}}{3}$

B. $\frac{a}{2}$

C. $\frac{a \sqrt{2}}{2}$

D. $\frac{a}{3}$

Xem đáp án

Chọn A

$Y C B T \Leftrightarrow Δ C J D$ vuông cân tại J

$\Leftrightarrow I J = I C = I D = \frac{A B}{2} \Leftrightarrow 4 x^{2} = 2 A I^{2} = 2 (\frac{a^{2} + a^{2}}{2} - x^{2}) \Leftrightarrow x = \frac{a \sqrt{3}}{3}$

( Với I là trung điểm CD; J là trung điểm AB)