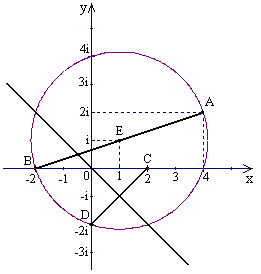
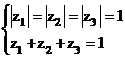Gọi A, B theo thứ tự là các điểm trong mặt
phẳng phức biểu diễn số phức là 4 + 2i, -2, . Khi đó tập hợp điểm M biểu diễn số phức z thỏa mãn (1) là đường tròn đường kính AB, trừ hai điểm A và B. Đường tròn này có tâm E biểu diễn số phức 1 + i và bán kính
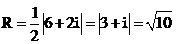
nên có phương trình là
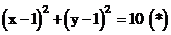
Gọi C, D theo thứ tự là các điểm trong mặt phẳng phức biểu diễn các số phức 2, - i. Khi đó tập hợp điểm M biểu diễn số phức z thỏa mãn (2) là đường trung trực của đoạn thẳng CD. Đường trung trực này đi qua trung điểm H (1, -i) của đoạn thẳng CD và nhận
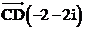
làm véctơ pháp tuyến nên có phương trình là
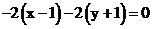
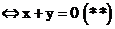
. Suy ra giao điểm của đường tròn và đường trung trực là nghiệm của hệ đã cho. Đó là các điểm (x;y) thỏa mãn (*) và (**), tức là nghiệm của hệ phương trình sau:
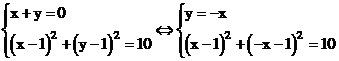
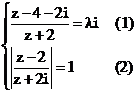
![]()
 Giải bởi Vietjack
Giải bởi Vietjack
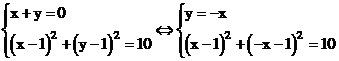
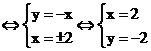 hoặc
hoặc 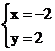 .
.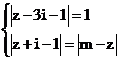 , (ẩn z là số phức)
, (ẩn z là số phức)