 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Phương pháp:
Sử dụng tính chất song song.
Cách giải:
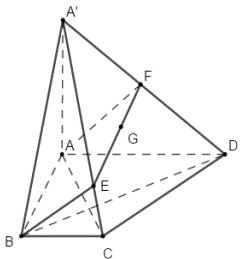
Từ G kẻ đường thẳng song song với AB lần lượt cắt SC, SD tại E, F.
Vậy thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng \(\left( {ABG} \right)\) là hình tứ giác ABEF.