Tìm khẳng định đúng trong các khẳng định sau.
A. Nếu một đường thẳng song song với một mặt phẳng thì nó song song với một đường thẳng nào đó nằm trong mặt phẳng đó.
B. Nếu hai mặt phẳng cùng song song với mặt phẳng thứ ba thì chúng song song với nhau.
D. Trong không gian, hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.
Giải bởi Vietjack
Chọn A
Cho tứ diện $ABCD$. Gọi $H,\,\,K$ lần lượt là trung điểm các cạnh $AB,\,\,BC.$ Trên đường thẳng $CD$ lấy điểm $M$ nằm ngoài đoạn $CD$. Thiết diện của tứ diện với mặt phẳng $(HKM)$ là
Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu $h\,{\text{(m)}}$ của mực nước trong kênh tính theo thời gian $t$ (giờ) trong một ngày $\left( {0 \leqslant t < 24} \right)$ cho bởi công thức \[h = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12.\] Tìm $t$ để độ sâu của mực nước là $9\,\,{\text{m}}$ (làm tròn đến chữ số thập phân thứ hai).
Cho hình chóp $S.ABC$. Gọi $L,\,\,M,\,\,N$ lần lượt các điểm trên các cạnh $SA,\,\,SB$ và $AC$ sao cho $LM$ không song song với $AB,\,\,LN$ không song song với $SC$. Mặt phẳng $(LMN)$ cắt các cạnh $AB,\,\,BC,\,\,SC$ lần lượt tại $K,\,\,I,\,\,J$. Ba điểm nào sau đây thẳng hàng?
Cho hình chóp $S.ABC$, gọi $M,\,\,P$ và $I$ lần lượt là trung điểm của $AB,\,\,SC$ và $SB$. Mặt phẳng $(\alpha )$ qua $MP$ và song song với $AC$ và cắt các cạnh $SA,\,\,BC$ tại $N,\,\,Q.$
a) Chứng minh đường thẳng $BC$ song sòng với mặt phẳng $(IMP)$.
b) Xác định thiết diện của $(\alpha )$ và hình chóp. Thiết diện này là hình gì?
c) Tìm giao điểm của đường thẳng $CN$ và mặt phẳng $(SMQ)$.
Người ta trồng $3\,\,003$ cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây. Hỏi có tất cả bao nhiêu cây?
Cho hình chóp $S.ABCD$ có đáy là hình thang với các cạnh đáy là $AB$ và $CD$. Gọi $I,\,\,J$ lần lượt là trung điểm của $AD$ và $BC$; $G$ là trọng tâm của tam giác $SAB.$ Giao tuyến của $(SAB)$ và $(IJG)$ là
Cho $\alpha $ thuộc góc phần phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai?
Cho góc $\alpha $ thỏa mãn $\cot \alpha = \frac{3}{4}$ và $0^\circ < \alpha < 90^\circ $. Khẳng định nào sau đây đúng?
Cho góc lượng giác $\left( {Oa,Ob} \right)$ có số đo là $50^\circ .$ Hỏi số đo của góc luọng giác nào trong bốn đáp án A, B, C, D bên dưới cũng có tia đầu là $Oa$ và tia cuối là $Ob?$
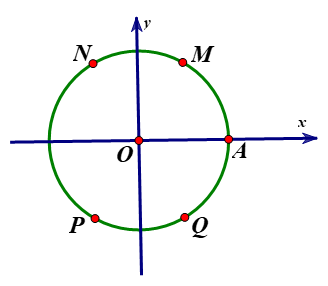
Trong mặt phẳng tọa độ $Oxy,$ trên đường tròn lượng giác như hình vẽ bên dưới. Điểm nào trong bốn đáp án A, B, C, D biểu diễn cho góc lượng giác có số đo bằng $60^\circ ?$
Điểm cuối của góc lượng giác $\alpha $ ở góc phần tư phần thứ mấy nếu $\sqrt {{{\sin }^2}\alpha } = \sin \alpha $.
