Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M là trung điểm SA, điểm N thuộc đoạn SD sao cho \[NS = 2ND,I\] là giao điểm của MN và AD.

a) Xác định giao tuyến của mặt phẳng \[\left( {BMN} \right)\] với mặt phẳng \[\left( {ABCD} \right)\].

b) Gọi J là giao điểm của CD với BI. Xác định giao tuyến của mặt phẳng \[\left( {BMN} \right)\] với mặt phẳng \[\left( {SCD} \right)\], từ đó suy ra thiết diện của hình chóp với mặt phẳng \[\left( {BMN} \right)\].

c) Gọi K là giao điểm của BI với AC. Chứng minh \[BM\parallel KN\].

Phương pháp:

a, b) Xác định 2 điểm chung của hai mặt phẳng.

c) Sử dụng định lí Ta-lét.

Cách giải:

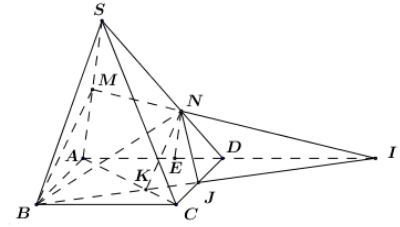
a)  Xét \[\left( {BMN} \right)\] và \[\left( {ABCD} \right)\] có:

+ B là điểm chung thứ nhất.

+ \[\left\{ \begin{array}{l}I \in MN \subset \left( {BMN} \right) \Rightarrow I \in \left( {BMN} \right)\\I \in AD \subset \left( {ABCD} \right) \Rightarrow I \in \left( {ABCD} \right)\end{array} \right. \Rightarrow I \in \left( {BMN} \right) \cap \left( {ABCD} \right) \Rightarrow I\] là điểm chung thứ hai.

Vậy \[\left( {BMN} \right) \cap \left( {ABCD} \right) = BI\]

b)  Xét \[\left( {BMN} \right)\] và \[\left( {SCD} \right)\] có:

+ N là điểm chung thứ nhất.

+ \[J = BI \cap CD \Rightarrow \left\{ \begin{array}{l}J \in BI \subset \left( {BMN} \right) \Rightarrow J \in \left( {BMN} \right)\\J \in CD \subset \left( {SCD} \right) \Rightarrow J \in \left( {SCD} \right)\end{array} \right. \Rightarrow J \in \left( {BMN} \right) \cap \left( {SCD} \right) \Rightarrow J\] là điểm chung thứ hai.

Vậy \[\left( {BMN} \right) \cap \left( {SCD} \right) = NJ\]. Từ đó ta có thiết diện của hình chóp cắt bởi \[\left( {BMN} \right)\] là tứ giác BMNJ.

c)  Trong \[\left( {SAD} \right)\] kẻ \[NE\parallel SA\left( {E \in AD} \right)\] ta có: \[\frac{{NE}}{{SA}} = \frac{{DN}}{{SD}} = \frac{1}{3} \Rightarrow \frac{{NE}}{{2MA}} = \frac{1}{3} \Leftrightarrow \frac{{NE}}{{MA}} = \frac{2}{3}\].

Mà \[\frac{{NE}}{{MA}} = \frac{{IN}}{{IM}} \Rightarrow \frac{{IN}}{{IM}} = \frac{2}{3} \Rightarrow \frac{{NI}}{{MN}} = 2\]

Mà IM là trung tuyến của tam giác \[SAI \Rightarrow N\] là trọng tâm tam giác SAI.

\[ \Rightarrow D\] là trung điểm của \[AI \Rightarrow \frac{{ID}}{{IA}} = \frac{1}{2} = \frac{{DJ}}{{AB}} = \frac{{DJ}}{{CD}} \Rightarrow J\] là trung điểm của CD.

\[ \Rightarrow \frac{{CJ}}{{AB}} = \frac{1}{2} = \frac{{KJ}}{{KB}} \Rightarrow KJ = \frac{1}{2}KB \Rightarrow IK = KJ + IJ = \frac{1}{2}KB + \frac{3}{2}KB = 2KB\]

Vậy \[\frac{{IN}}{{MN}} = \frac{{IK}}{{BK}} = 2 \Rightarrow BM\parallel KN\] (đpcm).