Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 6)
-
3910 lượt thi
-
18 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Dựa vào lý thuyết các hàm số lượng giác.
Cách giải:
Khẳng định đúng là đáp án C.
Câu 2:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Giải phương trình lượng giác cơ bản.
Cách giải:
\[\cos x = 1 \Leftrightarrow x = k2\pi \left( {k \in \mathbb{Z}} \right)\].
Câu 3:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
+ Sử dụng: \[{\sin ^2}x + {\cos ^2}x = 1\,\,\,\forall x \in \mathbb{R}\].
+ Giải phương trình lượng giác cơ bản.
+ Tìm các giá trị của \[k \in \mathbb{Z}\] để \[x \in \left[ { - \frac{\pi }{2};5\pi } \right]\].
Cách giải:
\[{\sin ^2}x + \cos 2x = - {\cos ^2}x \Leftrightarrow {\sin ^2}x + {\cos ^2}x + \cos 2x = 0\]
\[ \Leftrightarrow 1 + \cos 2x = 0 \Leftrightarrow \cos 2x = - 1 \Leftrightarrow 2x = \pi + k2\pi \Leftrightarrow x = \frac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)\]
\[x \in \left[ { - \frac{\pi }{2};5\pi } \right] \Rightarrow - \frac{\pi }{2} \le \frac{\pi }{2} + k\pi \le 5\pi \Leftrightarrow - \frac{1}{2} \le \frac{1}{2} + k \le 5 \Leftrightarrow - \frac{1}{5} \le k \le \frac{9}{2}\]
Mà \[k \in \mathbb{Z} \Rightarrow k \in \left\{ {0;1;2;3;4} \right\} \Rightarrow \] Phương trình ban đầu có 5 nghiệm thỏa mãn.
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng khái niệm chỉnh hợp.
Cách giải:
Số các số có 5 chữ số khác nhau lập được từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8 là một chỉnh hợp chập 5 của 8.
Vậy có \[A_8^5 = 6720\] số thỏa mãn.
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng khai triển nhị thức Niu – tơn: \[{\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n - k}}{b^k}} \]
Cách giải:
Ta có: \[{\left( {2 + x} \right)^{10}} = \sum\limits_{k = 0}^{10} {C_{10}^k{2^{10 - k}}{x^k}} \]
Hệ số của \[{x^3}\] ứng với \[k = 3\].
Vậy hệ số của \[{x^3}\] trong khai triển trên là: \[C_{10}^3{.2^7}\].
Câu 6:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
+ Tính số phần tử của không gian mẫu.
+ Tính số phần tử của biến cố.
+ Tính xác suất của biến cố.
Cách giải:
Chọn ngẫu nhiên một số nguyên dương nhỏ hơn 9 \[ \Rightarrow n\left( \Omega \right) = C_8^1 = 8\].
Gọi A là biến cố: “Số được chọn là số nguyên tố”.
Tập hợp các số nguyên tố là số nguyên dương nhỏ hơn 9 là \[\left\{ {2;3;5;7} \right\}\].
\[ \Rightarrow n\left( A \right) = C_4^1 = 4\].
Vậy \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{4}{8} = \frac{1}{2}\].
Câu 7:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Sử dụng công thức tổ hợp.
Cách giải:
\[C_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}}\]
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
\[{T_{\overrightarrow u }}\] biến \[M\left( {x;y} \right)\] thành \[M'\left( {x';y'} \right) \Rightarrow \left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\]
Cách giải:
\[{T_{\overrightarrow v }}\left( A \right) = A' \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = 1 + 2 = 3\\{y_{A'}} = 3 + 3 = 6\end{array} \right. \Rightarrow A'\left( {3;6} \right)\]
Câu 9:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
+ Xác định tâm I và bán kính R của đường tròn \[\left( C \right)\].
+ Gọi \[I' = {V_{\left( {O;2} \right)}}\left( I \right)\], xác định tọa độ \[I'\].
+ Gọi \[\left( {C'} \right) = {V_{\left( {O;2} \right)}}\left( C \right) \Rightarrow \left( {C'} \right)\] là đường tròn tâm \[I'\], bán kính \[R' = \left| k \right|.R\]
Cách giải:
+ Đường tròn \[\left( C \right)\] có tâm \[I\left( {1;1} \right),R = 2\].
+ Gọi \[I' = {V_{\left( {O;2} \right)}}\left( I \right) \Rightarrow \overrightarrow {OI'} = 2\overrightarrow {OI} \Rightarrow \left\{ \begin{array}{l}{x_{I'}} = 2.{x_I} = 2.1 = 2\\{y_{I'}} = 2.{y_I} = 2.1 = 2\end{array} \right. \Rightarrow I'\left( {2;2} \right)\]
+ Gọi \[\left( {C'} \right) = {V_{\left( {O;2} \right)}}\left( C \right) \Rightarrow \left( {C'} \right)\] là đường tròn tâm \[I'\left( {2;2} \right)\], bán kính \[R' = \left| k \right|.R = 2.2 = 4\]
Vậy phương trình đường tròn \[\left( {C'} \right):{\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 16\]
Câu 10:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Giao tuyến của hai mặt phẳng chứa hai đường thẳng song song là đường thẳng đi qua 1 điểm chung của hai mặt phẳng và song song với hai đường thẳng đó.
Cách giải:
Ta có \[\left\{ \begin{array}{l}Q \in \left( {PQR} \right)\\Q \in CD \subset \left( {ACD} \right) \Rightarrow Q \in \left( {ACD} \right)\end{array} \right. \Rightarrow Q \in \left( {PQR} \right) \cap \left( {ACD} \right)\]
\[\left\{ \begin{array}{l}\left( {PQR} \right) \supset PR\\\left( {ACD} \right) \supset AC\\PR\parallel AC\end{array} \right. \Rightarrow \] Giao tuyến của hai mặt phẳng \[\left( {PQR} \right)\] và \[\left( {ACD} \right)\]
là đường thẳng đi qua Q và song song với AC, PR.
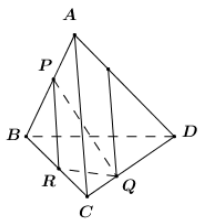
Câu 11:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Qua 3 điểm phân biệt không thẳng hàng xác định một mặt phẳng.
Cách giải:
Qua 3 điểm phân biệt không thẳng hàng xác định một mặt phẳng. Do đó số mặt phẳng tạo bởi 3 trong 5 điểm đã cho là: \[C_5^3 = 10\].
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
+ Xác định điểm I.
+ Xác định thiết diện.
+ Sử dụng công thức He-rong để tính diện tích tam giác: \[{S_{\Delta AEC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \].
Cách giải:
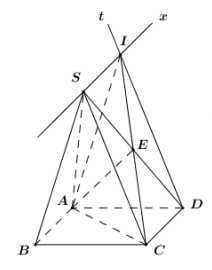
Trong \[\left( {SCD} \right)\] kẻ \[Dt\parallel SC\]
Ta có \[\left\{ \begin{array}{l}S \in \left( {SAB} \right) \cap \left( {SCD} \right)\\\left( {SAB} \right) \supset AB,\left( {SCD} \right) \supset CD\\AB\parallel CD\left( {gt} \right)\end{array} \right. \Rightarrow \] Giao tuyến của \[\left( {SAB} \right),\left( {SCD} \right)\] là đường thẳng đi qua S và song song với AB, CD. Trong \[\left( {SAB} \right)\] kẻ \[Sx\parallel AB \Rightarrow \left( {SAB} \right) \cap \left( {SCD} \right) = Sx\]
Trong \[\left( {SCD} \right)\] gọi \[I = Dt \cap Sx\] ta có: \[\left\{ \begin{array}{l}I \in Dt\\I \in Sx \subset \left( {SAB} \right) \Rightarrow I \in \left( {SAB} \right)\end{array} \right. \Rightarrow I = Dt \cap \left( {SAB} \right)\].
Trong \[\left( {SCD} \right)\] gọi \[E = CI \cap SD\], khi đó thiết diện của chóp cắt bởi \[\left( {AIC} \right)\] là tam giác AEC.
ABCD là hình vuông cạnh \[a \Rightarrow AC = a\sqrt 2 \].
Dễ dàng chứng minh được SBAI, SCDI là hình bình hành \[ \Rightarrow AI = SB = a,E\] là trung điểm của SD, IC.
Tam giác SAD có \[SA = AD = a,\angle SAD = 90^\circ \Rightarrow \Delta SAD\] vuông cân tại \[A \Rightarrow SD = SA\sqrt 2 = a\sqrt 2 \].
\[ \Rightarrow AE = \frac{1}{2}SD = \frac{{a\sqrt 2 }}{2}\]
Xét tam giác IAC có:
\[A{E^2} = \frac{{A{I^2} + A{C^2}}}{2} - \frac{{I{C^2}}}{4} \Leftrightarrow \frac{{{a^2}}}{2} = \frac{{{a^2} + 2{a^2}}}{2} - \frac{{I{C^2}}}{4}\]
\[ \Rightarrow \frac{{I{C^2}}}{4} = {a^2} \Leftrightarrow I{C^2} = 4{a^2} \Leftrightarrow IC = 2a \Rightarrow EC = \frac{1}{2}IC = a\]
Khi đó áp dụng công thức Hê-rông ta có: \[{S_{\Delta AEC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \frac{{{a^2}\sqrt 7 }}{8}\]
Câu 13:
Giải các phương trình sau:
a) \[\sin 2x = \frac{1}{2}\]
 Xem đáp án
Xem đáp án
Phương pháp:
Giải phương trình lượng giác cơ bản \[\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\]
Cách giải:
\[\sin 2x = \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{6} + k2\pi \\2x = \frac{{5\pi }}{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{12}} + k\pi \\x = \frac{{5\pi }}{{12}} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\]
Câu 14:
Giải các phương trình sau:
b) \[\sin x - \sqrt 3 \cos x = \sqrt 3 \]
 Xem đáp án
Xem đáp án
b) \[\sin x - \sqrt 3 \cos x = \sqrt 3 \]
Phương pháp:
Chia cả hai vế của phương trình cho \[\sqrt {{a^2} + {b^2}} \]
Cách giải:
\[\sin x - \sqrt 3 \cos x = \sqrt 3 \Leftrightarrow \frac{1}{2}\sin x - \frac{{\sqrt 3 }}{2}\cos x = \frac{{\sqrt 3 }}{2}\]
\[ \Leftrightarrow \sin x\cos \frac{\pi }{3} - \cos x\sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2} \Leftrightarrow \sin \left( {x - \frac{\pi }{3}} \right) = \sin \frac{\pi }{3}\]
\[ \Leftrightarrow \left[ \begin{array}{l}x - \frac{\pi }{3} = \frac{\pi }{3} + k2\pi \\x - \frac{\pi }{3} = \frac{{2\pi }}{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{2\pi }}{3} + k2\pi \\x = \pi + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\]
Câu 15:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng khai triển nhị thức Niu-tơn: \[{\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n - k}}{b^k}} \]
Cách giải:
Ta có: \[{\left( {{x^2} + \frac{2}{x}} \right)^8} = \sum\limits_{k = 0}^8 {C_8^k{{\left( {{x^2}} \right)}^{8 - k}}{{\left( {\frac{2}{x}} \right)}^k}} = \sum\limits_{k = 0}^8 {C_8^k{2^k}{x^{16 - 2k}}{x^{ - k}}} = \sum\limits_{k = 0}^8 {C_8^k{2^k}{x^{16 - 3k}}} \]
Số hạng chứa \[{x^7}\] ứng với \[16 - 3k = 7 \Leftrightarrow k = 3\left( {tm} \right)\].
Vậy hệ số của \[{x^7}\] trong khai triển trên là \[C_8^3{.2^3} = 448\].
Câu 16:
Trong ngân hàng đề có 6 câu hỏi dễ, 5 câu hỏi trung bình và 3 câu hỏi khó. Một đề thi gồm có 6 câu hỏi được chọn từ các câu trong ngân hàng đề đã cho.
a) Hỏi có tất cả bao nhiêu đề thi khác nhau nếu trong đề có 3 câu dễ, 2 câu trung bình và 1 câu khó.
 Xem đáp án
Xem đáp án
a) Hỏi có tất cả bao nhiêu đề thi khác nhau nếu trong đề có 3 câu dễ, 2 câu trung bình và 1 câu khó.
Phương pháp:
Sử dụng quy tắc nhân.
Cách giải:
Chọn 3 câu dễ có \[C_6^3\] cách.
Chọn 2 câu trung bình có \[C_5^2\] cách.
Chọn 1 câu khó có \[C_3^1\] cách.
Áp dụng quy tắc nhân ta tính được số đề thi thỏa mãn là \[C_6^3.C_5^2.C_3^1 = 600\].
Câu 17:
b) Nếu các câu hỏi trong đề thi được chọn ngẫu nhiên. Tính xác suất để trong đề thi có đủ ba loại câu hỏi sao cho số câu dễ và câu trung bình bằng nhau.
 Xem đáp án
Xem đáp án
b) Nếu các câu hỏi trong đề thi được chọn ngẫu nhiên. Tính xác suất để trong đề thi có đủ ba loại câu hỏi sao cho số câu dễ và câu trung bình bằng nhau.
Phương pháp:
+ Tính số phần tử của không gian mẫu.
+ Tính số phần tử của biến cố.
+ Tính xác suất của biến cố.
Cách giải:
Chọn 6 câu bất kì trong 14 câu \[ \Rightarrow n\left( \Omega \right) = C_{14}^6\].
Gọi A là biến cố: “Trong đề thi có đủ ba loại câu hỏi sao cho số câu dễ và câu trung bình bằng nhau.”
Do đó trong đề thi phải có 2 dễ + 2 trung bình + 2 khó \[ \Rightarrow n\left( A \right) = C_6^2.C_5^2.C_3^2 = 450\]
Vậy \[P\left( A \right) = \frac{{450}}{{C_{14}^6}} = \frac{{150}}{{1001}}\].
Câu 18:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M là trung điểm SA, điểm N thuộc đoạn SD sao cho \[NS = 2ND,I\] là giao điểm của MN và AD.
a) Xác định giao tuyến của mặt phẳng \[\left( {BMN} \right)\] với mặt phẳng \[\left( {ABCD} \right)\].
b) Gọi J là giao điểm của CD với BI. Xác định giao tuyến của mặt phẳng \[\left( {BMN} \right)\] với mặt phẳng \[\left( {SCD} \right)\], từ đó suy ra thiết diện của hình chóp với mặt phẳng \[\left( {BMN} \right)\].
c) Gọi K là giao điểm của BI với AC. Chứng minh \[BM\parallel KN\].
 Xem đáp án
Xem đáp án
Phương pháp:
a, b) Xác định 2 điểm chung của hai mặt phẳng.
c) Sử dụng định lí Ta-lét.
Cách giải:
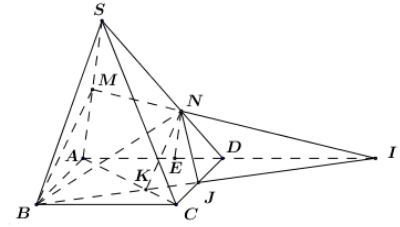
a) Xét \[\left( {BMN} \right)\] và \[\left( {ABCD} \right)\] có:
+ B là điểm chung thứ nhất.
+ \[\left\{ \begin{array}{l}I \in MN \subset \left( {BMN} \right) \Rightarrow I \in \left( {BMN} \right)\\I \in AD \subset \left( {ABCD} \right) \Rightarrow I \in \left( {ABCD} \right)\end{array} \right. \Rightarrow I \in \left( {BMN} \right) \cap \left( {ABCD} \right) \Rightarrow I\] là điểm chung thứ hai.
Vậy \[\left( {BMN} \right) \cap \left( {ABCD} \right) = BI\]
b) Xét \[\left( {BMN} \right)\] và \[\left( {SCD} \right)\] có:
+ N là điểm chung thứ nhất.
+ \[J = BI \cap CD \Rightarrow \left\{ \begin{array}{l}J \in BI \subset \left( {BMN} \right) \Rightarrow J \in \left( {BMN} \right)\\J \in CD \subset \left( {SCD} \right) \Rightarrow J \in \left( {SCD} \right)\end{array} \right. \Rightarrow J \in \left( {BMN} \right) \cap \left( {SCD} \right) \Rightarrow J\] là điểm chung thứ hai.
Vậy \[\left( {BMN} \right) \cap \left( {SCD} \right) = NJ\]. Từ đó ta có thiết diện của hình chóp cắt bởi \[\left( {BMN} \right)\] là tứ giác BMNJ.
c) Trong \[\left( {SAD} \right)\] kẻ \[NE\parallel SA\left( {E \in AD} \right)\] ta có: \[\frac{{NE}}{{SA}} = \frac{{DN}}{{SD}} = \frac{1}{3} \Rightarrow \frac{{NE}}{{2MA}} = \frac{1}{3} \Leftrightarrow \frac{{NE}}{{MA}} = \frac{2}{3}\].
Mà \[\frac{{NE}}{{MA}} = \frac{{IN}}{{IM}} \Rightarrow \frac{{IN}}{{IM}} = \frac{2}{3} \Rightarrow \frac{{NI}}{{MN}} = 2\]
Mà IM là trung tuyến của tam giác \[SAI \Rightarrow N\] là trọng tâm tam giác SAI.
\[ \Rightarrow D\] là trung điểm của \[AI \Rightarrow \frac{{ID}}{{IA}} = \frac{1}{2} = \frac{{DJ}}{{AB}} = \frac{{DJ}}{{CD}} \Rightarrow J\] là trung điểm của CD.
\[ \Rightarrow \frac{{CJ}}{{AB}} = \frac{1}{2} = \frac{{KJ}}{{KB}} \Rightarrow KJ = \frac{1}{2}KB \Rightarrow IK = KJ + IJ = \frac{1}{2}KB + \frac{3}{2}KB = 2KB\]
Vậy \[\frac{{IN}}{{MN}} = \frac{{IK}}{{BK}} = 2 \Rightarrow BM\parallel KN\] (đpcm).
