Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 16)
-
3663 lượt thi
-
23 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Đáp án A
Phương pháp:
Các đoạn giao tuyến giữa mặt phẳng và hình chóp khi nối tiếp nhau sẽ tạo thành một đa giác phẳng, người ta gọi đó là thiết diện (hay mặt cắt) của mặt phẳng với hình chóp đó.
Cách giải:
Chóp tứ giác có 5 mặt nên thiết diện tối đa chỉ có thể là ngũ giác, không thể là lục giác.
Câu 2:
Xem đáp án
Đáp án D
Phương pháp:
Hai điểm \[M\left( {a;b} \right)\] và \[M'\left( { - a;b} \right)\] đối xứng nhau qua trục Oy.
Cách giải:
Hai điểm \[M\left( {5; - 7} \right)\] và \[M'\left( { - 5; - 7} \right)\] đối xứng nhau qua trục Oy.
Câu 3:
Xem đáp án
Đáp án A
Phương pháp:
Qua ba điểm phân biệt không thẳng hàng xác định một mặt phẳng.
Cách giải:
Qua ba điểm phân biệt không thẳng hàng xác định một mặt phẳng nên số mặt phẳng phân biệt tạo bởi 3 trong số 2018 điểm trên là \[C_{2018}^3 = C_{2018}^{2015}.\]
Câu 4:
Xem đáp án
Đáp án A
Cách giải:
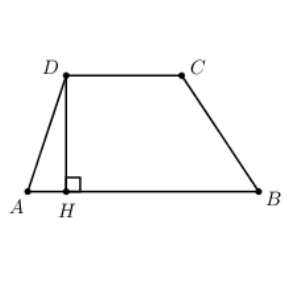
Vẽ \[DH \bot AB{\rm{ }}\left( {H \in AB} \right)\] ta có \[DH = \frac{{\sqrt 3 }}{2}.\]
Phương trình CD: \[y = \pm \frac{{\sqrt 3 }}{2}.\]
TH1: Phương trình CD: \[y = \frac{{\sqrt 3 }}{2}.\]
Khi đó tọa độ điểm C, D là nghiệm của phương trình
\[\cos y = \frac{{\sqrt 3 }}{2} \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + m2\pi \\x = - \frac{\pi }{6} + n2\pi \end{array} \right.\left( {m,n \in \mathbb{Z}} \right).\]
\[ \Rightarrow CD = \left| {{x_C} - {x_D}} \right| = \left| {\frac{\pi }{6} + m2\pi + \frac{\pi }{6} - n2\pi } \right| = \left| {\frac{\pi }{3} + \left( {m - n} \right)2\pi } \right|\]
\[ \Rightarrow \frac{\pi }{3} + \left( {m - n} \right)2\pi < \frac{\pi }{2} \Leftrightarrow \frac{1}{3} + 2\left( {m - n} \right) < \frac{1}{2} \Leftrightarrow m - n < \frac{1}{{12}}\]
Chọn \[m - n = 0 \Leftrightarrow CD = \frac{\pi }{3} \Rightarrow AB = \frac{{2\pi }}{3}.\]
TH2: Phương trình CD: \[y = - \frac{{\sqrt 3 }}{2} \Rightarrow \] Tọa độ của C, D là nghiệm của phương trình
\[\cos x = - \frac{{\sqrt 3 }}{2} \Leftrightarrow \left[ \begin{array}{l}x = \frac{{5\pi }}{6} + m'2\pi \\x = - \frac{{5\pi }}{6} + n'2\pi \end{array} \right.\left( {m',n' \in \mathbb{Z}} \right)\]
\[ \Rightarrow CD = \left| {{x_C} - {x_D}} \right| = \left| {\frac{{3\pi }}{2} + \left( {m' - n'} \right)2\pi } \right|\]
Khi \[m' - n' = 0 \Rightarrow CD = \frac{{3\pi }}{2} > \frac{\pi }{2}\left( {ktm} \right)\]
Khi \[m' - n' = - 1 \Rightarrow CD = \frac{\pi }{2} = \frac{\pi }{2}\left( {ktm} \right)\]
Vậy \[AB = \frac{{2\pi }}{3}.\]
Câu 5:
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng định lí: Hai mặt phẳng chứa hai đường thẳng song song thì cắt nhau theo giao tuyến (nếu có) song song với hai đường thẳng đó.
Cách giải:
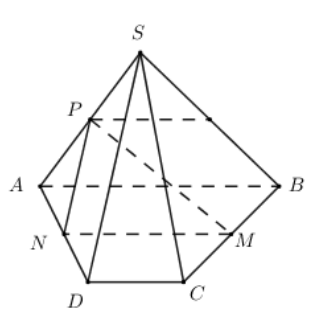
\[\left( {SAB} \right)\] và \[\left( {MNP} \right)\] có điểm P chung;
\[\left\{ \begin{array}{l}AB \subset \left( {SAB} \right)\\MN \subset \left( {MNP} \right)\\AB||MN\end{array} \right. \Rightarrow \] Giao tuyến của 2 mặt phẳng \[\left( {SAB} \right)\] và \[\left( {MNP} \right)\] là đường thẳng qua P và song song với AB.
Câu 6:
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng công thức SHTQ của CSC: \[{u_n} = {u_1} + \left( {n - 1} \right)d.\]
Cách giải:
Giả sử 2018 là số hạng thứ n ta có \[{u_n} = 2018 \Leftrightarrow 2 + \left( {n - 1} \right)9 = 2018 \Leftrightarrow n = 225.\]
Câu 7:
Xem đáp án
Đáp án A
Phương pháp:
Sử dụng công thức chỉnh hợp chập k của n.
Cách giải:
Số cách lấy ra từ hộp 3 quả cầu là \[C_{10}^3 = 120\] (cách).
Câu 8:
Xem đáp án
Đáp án C
Phương pháp:
Sử dụng khai triển nhị thức Newton: \[{\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^k}{b^{n - k}}.} \]
Cách giải:
Ta có: \[{\left( {x + 4} \right)^{20}} = \sum\limits_{k = 0}^{20} {C_{20}^k{x^k}{4^{20 - k}}.} \]
Số hạng chứa \[{x^{11}}\] tương ứng với \[k = 11.\]
Vậy số hạng chứa \[{x^{11}}\] là: \[C_{20}^{11}{.4^9}.{x^{11}} = C_{20}^9{.4^9}.{x^{11}}.\]
Chú ý: HS cần phân biệt số hạng chứa \[{x^{11}}\] và hệ số của số hạng chứa \[{x^{11}}\] để tránh chọn nhầm đáp án D.
Câu 9:
Xem đáp án
Đáp án
Phương pháp: C
Thay \[n = 2018.\]
Cách giải:
\[{u_n} = 1 + {2^n} \Rightarrow {u_{2018}} = 1 + {2^{2018}}.\]
Câu 10:
Xem đáp án
Đáp án B
Phương pháp:
Hàm phân thức xác định khi và chỉ khi mẫu thức khác 0.
Cách giải:
Hàm số \[\frac{1}{{\sin 2x}}\] xác định \[ \Leftrightarrow \sin 2x \ne 0 \Leftrightarrow 2x \ne k\pi \Leftrightarrow x \ne \frac{{k\pi }}{2}\left( {k \in \mathbb{Z}} \right).\]
Vậy TXĐ của hàm số là \[D = \mathbb{R}\backslash \left\{ {\frac{{k\pi }}{2},k \in \mathbb{Z}} \right\}.\]
Câu 11:
Xem đáp án
Đáp án A
Phương pháp:
Suy luận từng mệnh đề.
Cách giải:
Đáp án A sai vì Cho điểm M nằm ngoài mặt phẳng \[\left( \alpha \right).\] Khi đó tồn tại vô số đường thẳng a chứa M và song song với \[\left( \alpha \right).\] Các đường thẳng đó nằm trong mặt phẳng đi qua M và song song với \[\left( \alpha \right).\]
Câu 12:
Xem đáp án
Đáp án D
Phương pháp:
Giải phương trình lượng giác cơ bản: \[\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right).\]
Cách giải:
\[\sin x = \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi \\x = \frac{{5\pi }}{6} + l2\pi \end{array} \right.\left( {k,l \in \mathbb{Z}} \right)\]
\[0 \le \frac{\pi }{6} + k2\pi \le 20\pi \Leftrightarrow \frac{{ - 1}}{{12}} \le k \le \frac{{119}}{{12}} \Rightarrow k \in \left\{ {0;1;2;...;9} \right\}\]
\[0 \le \frac{{5\pi }}{6} + l2\pi \le 20\pi \Leftrightarrow \frac{{ - 5}}{{12}} \le k \le \frac{{115}}{{12}} \Rightarrow l \in \left\{ {0;1;2;...;9} \right\}\]
Vậy phương trình đã cho có 20 nghiệm thuộc \[\left[ {0;2\pi } \right].\]
Câu 13:
Xem đáp án
Đáp án D
Phương pháp:
Sử dụng quy tắc nhân.
Cách giải:
Số cách chọn 1 bạn nữ là \[C_2^1\] cách.
Số cách chọn 3 bạn nam là \[C_6^3\] cách.
Vậy số cách chọn 1 bạn nữ và 3 bạn nam là \[C_2^1.C_6^3 = 40\] cách.
Câu 14:
Xem đáp án
Đáp án C
Phương pháp:
Số chia hết cho 5 là số có tận cùng là 0 hoặc 5.
Cách giải:
Số các số tự nhiên có 3 chữ số là \[9.10.10 = 900\] số \[ \Rightarrow n\left( \Omega \right) = 900.\]
Gọi A là biến cố: “số được chọn không vượt quá 600, đồng thời nó chia hết cho 5”.
\[ \Rightarrow A = \left\{ {100 \le 5k \le 600|k \in \mathbb{N}} \right\}.\] Do \[100 \le 5k \le 600 \Leftrightarrow 20 \le k \le 120,\] suy ra có \[\frac{{120 - 20}}{1} + 1 = 101\] số k thỏa mãn \[ \Rightarrow n\left( A \right) = 101.\]
Vậy \[P\left( A \right) = \frac{{101}}{{900}}.\]
Câu 15:
Xem đáp án
Đáp án B
Phương pháp:
Chứng minh dãy số đã cho là dãy số giảm bằng cách chứng minh hiệu \[{u_{n + 1}} - {u_n} < 0.\] Từ đó chọn kết luận đúng.
Cách giải:
Ta có
\[{u_n} = \frac{{n + 2018}}{{2018n + 1}} = \frac{{n + \frac{1}{{2018}} + 2018 - \frac{1}{{2018}}}}{{2018n + 1}}\]
\[ = \frac{1}{{2018}} + \frac{{2018 - \frac{1}{{2018}}}}{{2018n + 1}} = \frac{1}{{2018}} + \frac{{{{2018}^2} - 1}}{{2018\left( {2018n + 1} \right)}} = \frac{1}{{2018}} + \frac{{2017.2019}}{{2018\left( {2018n + 1} \right)}}\]
\[ \Rightarrow {u_{n + 1}} = \frac{1}{{2018}} + \frac{{2017.2019}}{{2018\left( {2018\left( {n + 1} \right) + 1} \right)}}\]
\[ = \frac{1}{{2018}} + \frac{{2017.2019}}{{2018\left( {2018n + 2019} \right)}}\]
\[ \Rightarrow {u_{n + 1}} - {u_n}\]
\[ = \frac{{2017.2019}}{{2018\left( {2018n + 2019} \right)}} - \frac{{2017.2019}}{{2018\left( {2018n + 1} \right)}}\]
\[ = \frac{{2017.2019}}{{2018}}\left( {\frac{1}{{2018n + 2019}} - \frac{1}{{2018n + 1}}} \right)\]
Do \[2018n + 2019 > 2018n + 1 \Rightarrow \frac{1}{{2018n + 2019}} < \frac{1}{{2018n + 1}}\]
\[ \Rightarrow \frac{1}{{2018n + 2019}} - \frac{1}{{2018n + 1}} < 0\] hay \[{u_{n + 1}} - {u_n} < 0 \Leftrightarrow {u_{n + 1}} < {u_n}.\]
Suy ra dãy số đó cho là dãy số giảm.
Lại có \[{u_1} = \frac{{1 + 2018}}{{2018 + 1}} = 1.\] Vậy dãy số \[\left( {{u_n}} \right)\] giảm và bị chặn dưới bởi 1.
Câu 16:
Xem đáp án
Đáp án C
Phương pháp:
Sử dụng quy tắc nhân.
Cách giải:
Gọi số có hai chữ số cuối của SĐT cần tìm là \[\overline {ab} .\] Do hai chữ số đó phân biệt khác 0 nên có \[9.8 = 72\] cách chọn.
Vậy xác suất để người đó gọi một lần đúng số cần gọi là \[\frac{1}{{72}}.\]
Câu 17:
Xem đáp án
Đáp án C
Phương pháp:
Sử dụng công thức SHTQ của CSN: \[{u_n} = {u_1}{q^{n - 1}}.\]
Cách giải:
Ta có: \[{U_2} = {U_1}.q \Rightarrow {U_1} = \frac{{{U_2}}}{q} = \frac{5}{2}\]
\[ \Rightarrow {U_7} = {U_1}.{q^6} = \frac{5}{2}{.2^6} = 160.\]
Câu 18:
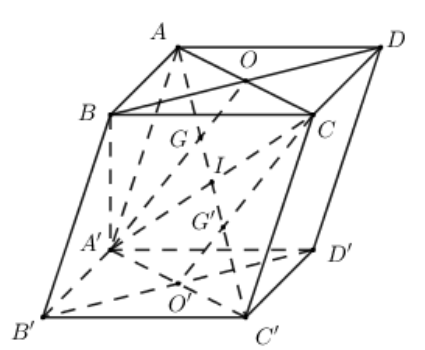
Cho hình hộp \[ABCD.A',B',C',D'\]. Gọi G và G’ là trọng tâm các tam giác \[BDA'\] và \[A'CC'\].
Khẳng định nào sau đây đúng?
Xem đáp án
Đáp án D
Phương pháp:
Sử dụng định lí Ta-lét.
Cách giải:
Gọi \[O = AC \cap BD,O' = A'C' \cap B'D'.\] Gọi \[I = AC' \cap A'C.\]
Do \[ACC'A'\] là hình bình hành \[ \Rightarrow \] I là trung điểm của \[A'C\]
\[ \Rightarrow G \in AI \Rightarrow G \in AC'.\] Chứng minh tương tự ta có \[G' \in AC'.\]
Do G là trọng tâm tam giác \[BDA'\] nên \[\frac{{A'G}}{{OG}} = 2.\]
Áp dụng định lí Ta-lét ta có: \[\frac{{A'G}}{{OG}} = \frac{{GC'}}{{AG}} = 2 \Rightarrow AG = \frac{1}{3}AC'.\]
Chứng minh tương tự ta có \[G'C' = \frac{1}{3}AC'.\] Vậy \[GG' = \frac{1}{3}AC'.\]
Câu 19:
Xem đáp án
Đáp án C
Phương pháp:
Sử dụng khai triển nhị thức Newton \[{\left( {x + 1} \right)^{2018}}\] và cho \[x = - 1.\]
Cách giải:
Ta có: \[{\left( {x + 1} \right)^{2018}} = \sum\limits_{k = 0}^{2018} {C_{2018}^k} {x^k}.\]
Với \[x = - 1\] ta có \[0 = \sum\limits_{k = 0}^{2018} {C_{2018}^k} {\left( { - 1} \right)^k} = C_{2018}^0 - C_{2018}^1 + C_{2018}^2 + ... - C_{2018}^{2017} + C_{2018}^{2018}\]
\[ \Rightarrow C_{2018}^0 - C_{2018}^1 + C_{2018}^2 + ... - C_{2018}^{2017} = - C_{2018}^{2018} = - 1.\]
Câu 20:
Xem đáp án
Đáp án D
Phương pháp:
Sử dụng công thức \[A_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}\]
Cách giải:
Số cách chọn 3 học sinh trong tổ để làm ba việc khác nhau là 1 chỉnh hợp chập 3 của n, khi đó ta có:
\[A_n^3 = 210 \Leftrightarrow \frac{{n!}}{{\left( {n - 3} \right)!}} = 210 \Leftrightarrow n\left( {n - 1} \right)\left( {n - 2} \right) = 210.\]
Câu 21:
Xem đáp án
Phương pháp:
+) Sử dụng công thức biến đổi tổng thành tích \[\sin a - \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a - b}}{2}.\]
+) Đưa phương trình đã cho về dạng tích sau đó giải phương trình lượng giác cơ bản.
Cách giải:
\[\frac{{\sin 3x - \sin x + \sin 2x}}{{2\cos x - 1}} = 0.\]
ĐK: \[2\cos x - 1 \ne 0 \Leftrightarrow \cos x \ne \frac{1}{2} \Leftrightarrow x \ne \pm \frac{\pi }{3} + k2\pi \left( {k \in \mathbb{Z}} \right).\]
\[pt \Leftrightarrow \sin 3x - \sin x + \sin 2x = 0\]
\[ \Leftrightarrow 2\cos 2x\sin x + 2\sin x\cos x = 0\]
\[ \Leftrightarrow 2\sin x\left( {\cos x + \cos 2x} \right) = 0 \Leftrightarrow 2\sin x\left( {2{{\cos }^2}x + \cos x - 1} \right) = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}\sin x = 0\\\cos x = - 1\\\cos x = - \frac{1}{2}\left( {loai} \right)\end{array} \right. \Leftrightarrow \sin x = 0 \Rightarrow A = \sin x = 0\]
Vậy A = 0
Câu 22:
Xem đáp án
Phương pháp:
+) Gọi d là công sai của cấp số cộng trên, sử dụng công thức tính tổng n số hạng đầu tiên của cấp số cộng \[{S_n} = \frac{{\left[ {2{u_1} + \left( {n - 1} \right)d} \right].n}}{2}\] tìm d.
+) Viết công thức của SHTQ của CSC.
+) Tính \[\frac{1}{{{u_k}{u_{k + 1}}}},\] rút gọn sau đó tính S.
Cách giải:
Gọi d là công sai của cấp số cộng trên ta có:
\[{S_n} = \frac{{\left[ {2{u_1} + \left( {n - 1} \right)d} \right].n}}{2} \Rightarrow {S_{100}} = \frac{{\left( {2 + 99d} \right).100}}{2} = 10000 \Rightarrow d = 2.\]
Khi đó ta có số hạng tổng quát của cấp số cộng là \[{u_n} = 1 + \left( {n - 1} \right).2 = 2n - 1.\]
Xét \[{u_k}{u_{k + 1}} = \frac{1}{{\left( {2k - 1} \right)\left( {2k + 1} \right)}} = \frac{1}{2}\left( {\frac{1}{{2k - 1}} - \frac{1}{{2k + 1}}} \right).\] Khi đó ta có:
\[S = \frac{1}{2}\left( {1 - \frac{1}{3} + \frac{1}{3} - \frac{1}{5} + ... + \frac{1}{{197}} - \frac{1}{{199}}} \right)\]
\[ \Rightarrow S = \frac{1}{2}\left( {1 - \frac{1}{{199}}} \right) = \frac{{99}}{{199}}\]
Vậy \[S = \frac{{99}}{{199}}.\]
Câu 23:
Cho hình chóp \[S.ABCD\] có đáy là hình thang, \[AB//CD\] và \[AB = 2CD\]. Gọi O là giao điểm của AC và BD. Lấy E thuộc cạnh SA, F thuộc cạnh SC sao cho \[\frac{{SE}}{{SA}} = \frac{{SF}}{{SC}} = \frac{2}{3}\].
a) Chứng minh đường thẳng AC song song với mặt phẳng \[\left( {BEF} \right)\].
b) Xác định giao điểm N của đường thẳng SD với mặt phẳng \[\left( {BEF} \right)\] , từ đó chỉ ra thiết diện của hình chóp cắt bởi mặt phẳng \[\left( {BEF} \right)\].
c) Gọi \[\left( \alpha \right)\] là mặt phẳng qua O và song song với mặt phẳng \[\left( {BEF} \right)\]. Gọi P là giao điểm của SD với \[\left( \alpha \right)\]. Tính tỉ số \[\frac{{SP}}{{SD}}\].
Xem đáp án
Phương pháp:
a) Một đường thẳng song song với một mặt phẳng khi nó song song với một đường nằm trong mặt phẳng đó.
b) Xác định điểm chung của SD với \[\left( {BEF} \right),\] từ đó xác định thiết diện.
c) Xác định \[\left( \alpha \right).\] Sử dụng định lí Ta-lét.
Cách giải:
a) Áp dụng định lí Ta-lét đảo ta có \[\frac{{SE}}{{SA}} = \frac{{SF}}{{SC}} = \frac{2}{3} \Rightarrow EF{\rm{ // }}AC.\]
Mà \[EF \subset \left( {BEF} \right) \Rightarrow AC{\rm{ // }}\left( {BEF} \right).\]
b) Trong \[\left( {SAC} \right)\] gọi
\[I = SO \cap EF \Rightarrow \left\{ \begin{array}{l}I \in EF \Rightarrow I \in \left( {BEF} \right) \Rightarrow BI \subset \left( {BEF} \right)\\I \in SO \subset \left( {SBD} \right) \Rightarrow I \in \left( {SBD} \right)\end{array} \right..\]
Trong \[\left( {SBD} \right)\] gọi \[N = BI \cap SD\] ta có:
\[\left\{ \begin{array}{l}N \in SD\\N \in BI \subset \left( {BEF} \right)\end{array} \right. \Rightarrow N = SD \cap \left( {BEF} \right).\]
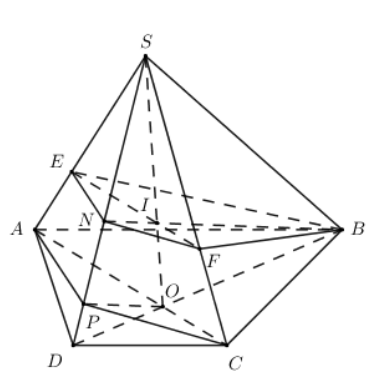
Ta có \[\left\{ \begin{array}{l}\left( {BEF} \right) \cap \left( {SAB} \right) = BE\\\left( {BEF} \right) \cap \left( {SAD} \right) = EN\\\left( {BEF} \right) \cap \left( {SCD} \right) = NF\\\left( {BEF} \right) \cap \left( {SBC} \right) = FB\end{array} \right. \Rightarrow \] Thiết diện của hình chóp cắt bởi mặt phẳng \[\left( {BEF} \right)\] là tứ giác BENF.
c) Ta có AC qua O và \[AC{\rm{ // }}EF \Rightarrow AC \subset \left( \alpha \right).\]
Trong \[\left( {SAD} \right)\] qua A kẻ \[AP{\rm{ // }}EN\left( {P \in SD} \right) \Rightarrow AP{\rm{ // }}\left( {BEF} \right) \Leftrightarrow AP \subset \left( \alpha \right).\]
Khi đó ta có \[\left( \alpha \right) \equiv \left( {BEF} \right).\]
Ta có \[\left\{ \begin{array}{l}\left( \alpha \right) \cap \left( {SBD} \right) = OP\\\left( {BEF} \right) \cap \left( {SBD} \right) = BN\\\left( \alpha \right){\rm{ // }}\left( {BEF} \right)\end{array} \right. \Rightarrow OP{\rm{ // }}BN.\]
Áp dụng đinh lí Ta-lét ta có: \[\frac{{DP}}{{DN}} = \frac{{DO}}{{DB}}.\]
Ta có: \[\frac{{DO}}{{OB}} = \frac{{DC}}{{AB}} = \frac{1}{2} \Rightarrow \frac{{DO}}{{DB}} = \frac{1}{3} \Rightarrow \frac{{DP}}{{DN}} = \frac{1}{3} \Rightarrow \frac{{DP}}{{PN}} = \frac{1}{2} \Rightarrow DP = \frac{1}{2}NP.\]
Lại áp dụng định lí Ta-lét ta có: \[\frac{{SN}}{{SP}} = \frac{{SE}}{{SA}} = \frac{2}{3}\left( {AP{\rm{ // }}EN} \right) \Rightarrow \frac{{SN}}{{NP}} = 2 \Rightarrow SN = 2NP.\]
Từ đó ta có \[\frac{{SP}}{{SD}} = \frac{{SN + NP}}{{SN + NP + DP}} = \frac{{2NP + NP}}{{2NP + NP + \frac{1}{2}NP}} = \frac{{3NP}}{{\frac{7}{2}NP}} = \frac{6}{7}.\]
Vậy \[\frac{{SP}}{{SD}} = \frac{6}{7}.\]