 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Phương pháp:
Sử dụng định lí: Hai mặt phẳng chứa hai đường thẳng song song thì cắt nhau theo giao tuyến (nếu có) song song với hai đường thẳng đó.
Cách giải:
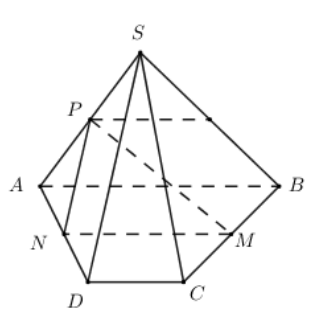
\[\left( {SAB} \right)\] và \[\left( {MNP} \right)\] có điểm P chung;
\[\left\{ \begin{array}{l}AB \subset \left( {SAB} \right)\\MN \subset \left( {MNP} \right)\\AB||MN\end{array} \right. \Rightarrow \] Giao tuyến của 2 mặt phẳng \[\left( {SAB} \right)\] và \[\left( {MNP} \right)\] là đường thẳng qua P và song song với AB.
Cho hình chóp \[S.ABCD\] có đáy là hình thang, \[AB//CD\] và \[AB = 2CD\]. Gọi O là giao điểm của AC và BD. Lấy E thuộc cạnh SA, F thuộc cạnh SC sao cho \[\frac{{SE}}{{SA}} = \frac{{SF}}{{SC}} = \frac{2}{3}\].
a) Chứng minh đường thẳng AC song song với mặt phẳng \[\left( {BEF} \right)\].
b) Xác định giao điểm N của đường thẳng SD với mặt phẳng \[\left( {BEF} \right)\] , từ đó chỉ ra thiết diện của hình chóp cắt bởi mặt phẳng \[\left( {BEF} \right)\].
c) Gọi \[\left( \alpha \right)\] là mặt phẳng qua O và song song với mặt phẳng \[\left( {BEF} \right)\]. Gọi P là giao điểm của SD với \[\left( \alpha \right)\]. Tính tỉ số \[\frac{{SP}}{{SD}}\].