 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Cách giải:
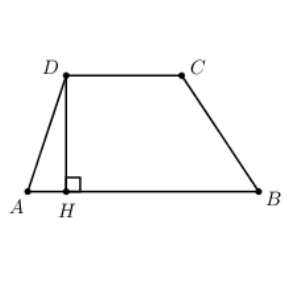
Vẽ \[DH \bot AB{\rm{ }}\left( {H \in AB} \right)\] ta có \[DH = \frac{{\sqrt 3 }}{2}.\]
Phương trình CD: \[y = \pm \frac{{\sqrt 3 }}{2}.\]
TH1: Phương trình CD: \[y = \frac{{\sqrt 3 }}{2}.\]
Khi đó tọa độ điểm C, D là nghiệm của phương trình
\[\cos y = \frac{{\sqrt 3 }}{2} \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + m2\pi \\x = - \frac{\pi }{6} + n2\pi \end{array} \right.\left( {m,n \in \mathbb{Z}} \right).\]
\[ \Rightarrow CD = \left| {{x_C} - {x_D}} \right| = \left| {\frac{\pi }{6} + m2\pi + \frac{\pi }{6} - n2\pi } \right| = \left| {\frac{\pi }{3} + \left( {m - n} \right)2\pi } \right|\]
\[ \Rightarrow \frac{\pi }{3} + \left( {m - n} \right)2\pi < \frac{\pi }{2} \Leftrightarrow \frac{1}{3} + 2\left( {m - n} \right) < \frac{1}{2} \Leftrightarrow m - n < \frac{1}{{12}}\]
Chọn \[m - n = 0 \Leftrightarrow CD = \frac{\pi }{3} \Rightarrow AB = \frac{{2\pi }}{3}.\]
TH2: Phương trình CD: \[y = - \frac{{\sqrt 3 }}{2} \Rightarrow \] Tọa độ của C, D là nghiệm của phương trình
\[\cos x = - \frac{{\sqrt 3 }}{2} \Leftrightarrow \left[ \begin{array}{l}x = \frac{{5\pi }}{6} + m'2\pi \\x = - \frac{{5\pi }}{6} + n'2\pi \end{array} \right.\left( {m',n' \in \mathbb{Z}} \right)\]
\[ \Rightarrow CD = \left| {{x_C} - {x_D}} \right| = \left| {\frac{{3\pi }}{2} + \left( {m' - n'} \right)2\pi } \right|\]
Khi \[m' - n' = 0 \Rightarrow CD = \frac{{3\pi }}{2} > \frac{\pi }{2}\left( {ktm} \right)\]
Khi \[m' - n' = - 1 \Rightarrow CD = \frac{\pi }{2} = \frac{\pi }{2}\left( {ktm} \right)\]
Vậy \[AB = \frac{{2\pi }}{3}.\]
Cho hình chóp \[S.ABCD\] có đáy là hình thang, \[AB//CD\] và \[AB = 2CD\]. Gọi O là giao điểm của AC và BD. Lấy E thuộc cạnh SA, F thuộc cạnh SC sao cho \[\frac{{SE}}{{SA}} = \frac{{SF}}{{SC}} = \frac{2}{3}\].
a) Chứng minh đường thẳng AC song song với mặt phẳng \[\left( {BEF} \right)\].
b) Xác định giao điểm N của đường thẳng SD với mặt phẳng \[\left( {BEF} \right)\] , từ đó chỉ ra thiết diện của hình chóp cắt bởi mặt phẳng \[\left( {BEF} \right)\].
c) Gọi \[\left( \alpha \right)\] là mặt phẳng qua O và song song với mặt phẳng \[\left( {BEF} \right)\]. Gọi P là giao điểm của SD với \[\left( \alpha \right)\]. Tính tỉ số \[\frac{{SP}}{{SD}}\].