Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 10)
-
3815 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công bội \(q\) thì \({u_n} = {u_1}.{q^{n - 1}};\,{u_n} = {u_{n - 1}}q\)
Cách giải:
Đáp án A: Ta nhận thấy \(2:1 = 2;\,\left( { - 4} \right):2 = - 2\) nên dãy số \(1,\,2,\, - 4,\,8\) không là một cấp số nhân
Đáp án B: Ta thấy \(2:\left( { - \sqrt 2 } \right) = - 2\sqrt 2 :2 = 4:\left( { - 2\sqrt 2 } \right) = - \sqrt 2 \) nên dãy số \( - \sqrt 2 ;\,2;\,2\sqrt 2 ;\,4\) là một cấp số nhân có \({u_1} = - \sqrt 2 \); công bội \(q = - \sqrt 2 \).
Đáp án C: Ta thấy \( - \sqrt 3 :3 \ne \left( { - 1} \right):\left( { - \sqrt 3 } \right)\) nên dãy số \(3;\,\sqrt 3 ;\,1;\,\frac{{\sqrt 3 }}{3}\)không là cấp số nhân
Đáp án D: Ta thấy \(5:10 = \frac{1}{2} \ne \frac{1}{5}\) nên dãy số 10, 5, 1, 1 không là cấp số nhân.
Câu 2:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp
Sử dụng công thức khai triển nhị thức Newton \({\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n - k}}{b^k}} \) và suy ra số số hạng của khai triển là \(n + 1\)
Cách giải:
Số số hạng của biểu thức \(P\left( x \right) = {\left( {2x + 1} \right)^{17}}\) là \(17 + 1 = 18\) số hạng.
Câu 3:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp
Hàm số \(y = \cot x\) có TXĐ \(D = \mathbb{R}\backslash \left\{ {k\pi ,\,k \in \mathbb{Z}} \right\}\).
Cách giải:
ĐK: \(\sin \frac{x}{2} \ne 0 \Leftrightarrow \frac{x}{2} \ne k\pi \Leftrightarrow x \ne k2\pi \left( {k \in \mathbb{Z}} \right)\)
Nên hàm số \(y = \cot \frac{x}{2}\) có TXĐ \(D = \mathbb{R}\backslash \left\{ {k2\pi ,\,k \in \mathbb{Z}} \right\}\).
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Sử dụng lý thuyết về tính chẵn lẻ của các hàm số lượng giác.
Cách giải:
Đáp án A: Hàm số \(y = \tan x\) là hàm số lẻ nên A sai.
Đáp án B: Hàm số \(y = \sin 2x\) là hàm số lẻ nên B đúng.
Đáp án C: Hàm số \(y = \cot 2x\) là hàm số lẻ trên \(\mathbb{R}\backslash \left\{ {\frac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\) nên C sai.
Đáp án D : Hàm số \(y = \cos x\) là hàm số chẵn trên \(\mathbb{R}\)nên D sai.
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp
Vận dụng đúng công thức \({u_n} = {2^n}\) để suy ra câu đúng.
Cách giải:
Ta có \({u_n} = {2^n}\) nên \({u_{n + 2}} = {2^{n + 2}} = {2^n}{.2^2} = {4.2^n}\)
Câu 6:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp
Sử dụng các tính chất của giai thừa, tổ hợp chập k của n.
Cách giải:
Đáp án A: sai vì \(C_n^0 = 1\).
Đáp án B: sai vì \(C_n^k = C_n^{n - k}\).
Đáp án C: sai vì \(0! = 1\).
Đáp án D đúng.
Câu 7:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Sử dụng vị trí tương đối của hai mặt phẳng trong không gian.
Cách giải:
Hai mặt phẳng trong không gian có thể có ba vị trí tương đối sau:
+ Song song
+ Cắt nhau
+ Trùng nhau
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Cứ mỗi cách chọn ra 3 điểm không thẳng hàng ta lại có được một tam giác.
Cách giải:
Do 2019 điểm phân biệt trên đường tròn nên không có 3 điểm nào thẳng hàng.
Mỗi cách chọn 3 trong 2019 điểm ta được một tam giác nên số tam giác là số cách chọn 3 trong 2019 điểm.
Vậy có \(C_{2019}^3\) tam giác.
Câu 9:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp
Sử dụng kiến thức về đường thẳng cắt mặt phẳng, đường thẳng song song với mặt phẳng
Cách giải:
A. Nếu đường thẳng a không có điểm chung với mặt phẳng \(\left( \alpha \right)\) thì \(a//\left( \alpha \right)\) nên A đúng.
B. Sai vì đường thẳng a có thể nằm trong \(\left( \alpha \right)\)
C. Sai vì đường thẳng a có thể nằm trong \(\left( \alpha \right)\)
D. Sai vì a, b có thể cắt nhau.
Câu 10:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Nhận xét tính đúng sai của mỗi đáp án, sử dụng tính chất hàm số sin.
Cách giải:
Đáp án A: đúng vì \(\sin \left( { - 3x} \right) = - \sin 3x\).
Đáp án B: sai vì hàm số có tập giá trị là \(\left[ { - 1;1} \right]\).
Đáp án C: đúng.
Đáp án D: đúng vì \(\sin \left( {3.0} \right) = 0\) nên đồ thị hàm số đi qua điểm \(\left( {0;0} \right)\).
Câu 11:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Tính xác suất theo định nghĩa \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\) với \(n\left( A \right)\) là số phần tử của biến cố A và \(n\left( \Omega \right)\) là số phần tử của không gian mẫu.
Cách giải:
Số phần tử của không gian mẫu: \(n\left( \Omega \right) = 6.6 = 36\)
Gọi A là biến cố: Tổng số chấm xuất hiện trên hai con súc sắc là 7
Có các cặp số có tổng là 7 là \(\left( {1;6} \right),\,\left( {6;1} \right),\,\left( {2;5} \right),\,\left( {5;2} \right),\,\left( {3;4} \right),\,\left( {4;3} \right)\)
Nên số phần tử của biến cố A là \(n\left( A \right) = 6\)
Xác suất cần tìm là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{6}{{36}} = \frac{1}{6}\)
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp
Sử dụng điều kiện đường thẳng song song mặt phẳng nếu nó không nằm trong mặt phẳng và song song với một đường thẳng nằm trong mặt phẳng đó.
Cách giải:
Đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\) nếu \(\left\{ \begin{array}{l}a//b\\b \subset \left( P \right)\\a \not\subset \left( P \right)\end{array} \right.\)
Câu 13:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Sử dụng công thức tọa độ của phép quay tâm \(O\left( {0;0} \right)\) góc quay \(\alpha \) biến \(M\left( {x;y} \right)\) thành \(M\left( {x';y'} \right)\) thì \(\left\{ \begin{array}{l}x' = x\cos \alpha - y\sin \alpha \\y' = x\sin \alpha + y\cos \alpha \end{array} \right.\)
Cách giải:
Ta có \({Q_{\left( {O; - 90^\circ } \right)}}\left( A \right) = A'\)
Suy ra \(\left\{ \begin{array}{l}{x_{A'}} = {x_A}\cos \left( { - 90^\circ } \right) - {y_A}\sin \left( { - 90^\circ } \right)\\{y_{A'}} = {x_A}\sin \left( { - 90^\circ } \right) + {y_A}\cos \left( { - 90^\circ } \right)\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = 2.0 - 0.\left( { - 1} \right) = 0\\{y_{A'}} = 2.\left( { - 1} \right) + 0.0 = - 2\end{array} \right.\) nên \(A'\left( {0; - 2} \right)\)
Câu 14:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp
Dựng hình, tìm ảnh của \(O\) qua phép tịnh tiến theo véc tơ \(\overrightarrow {BO} \).
Sử dụng định nghĩa: \({T_{\overrightarrow v }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'} = \overrightarrow v \)
Cách giải:
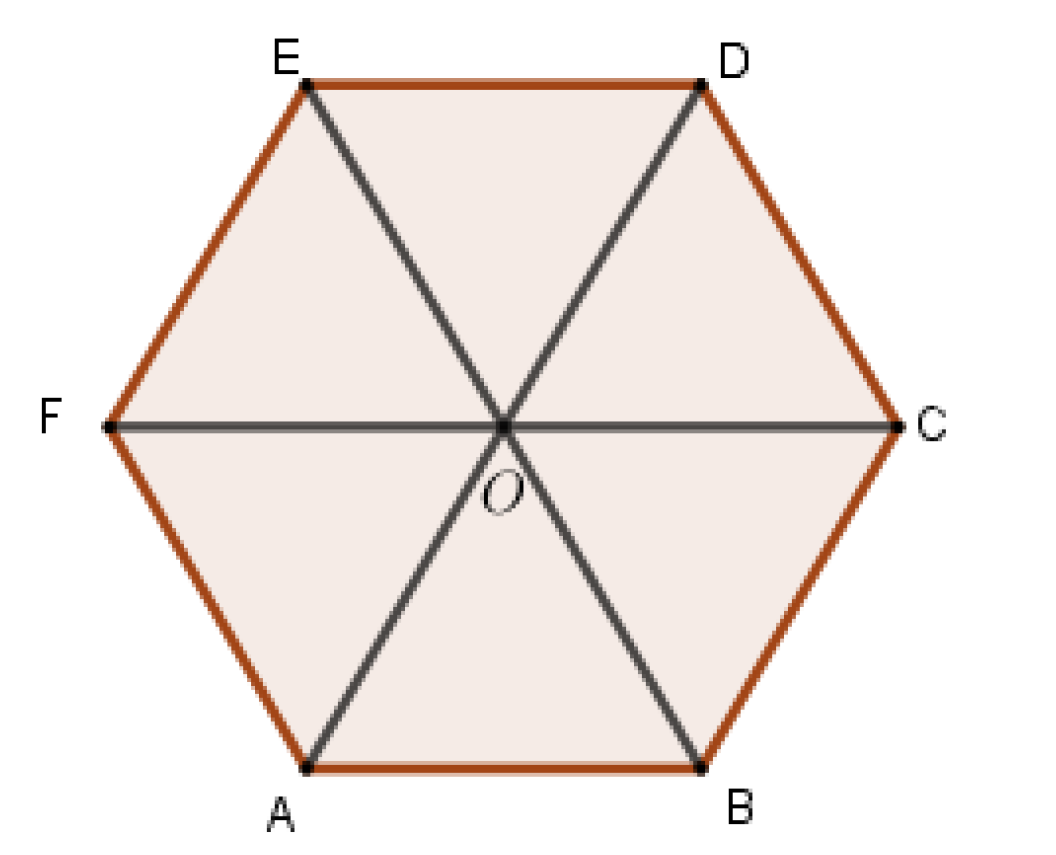
Quan sát hình vẽ ta thấy \({T_{\overrightarrow {BO} }}\left( O \right) = E\)vì \(\overrightarrow {OE} = \overrightarrow {BO} \)
Câu 15:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp
Đưa về giải phương trình dạng \[cos\left( {x - \alpha } \right) = 0 \Leftrightarrow x - \alpha = \frac{\pi }{2} + k\pi \] \(\left( {k \in \mathbb{Z}} \right)\)
Lưu ý: \(\cos \left( {a - b} \right) = \cos a\cos b + \sin a\sin b\)
Cách giải:
Ta có \(\sqrt 3 \sin x + \cos x = 0 \Leftrightarrow \frac{1}{2}\cos x + \frac{{\sqrt 3 }}{2}\sin x = 0 \Leftrightarrow \cos x.\cos \frac{\pi }{3} + \sin x.\sin \frac{\pi }{3} = 0\)
\( \Leftrightarrow \cos \left( {x - \frac{\pi }{3}} \right) = 0 \Leftrightarrow x - \frac{\pi }{3} = \frac{\pi }{2} + k\pi \Leftrightarrow x = \frac{{5\pi }}{6}\left( {k \in \mathbb{Z}} \right) \Leftrightarrow x = - \frac{\pi }{6} + k\pi \,\left( {k \in \mathbb{Z}} \right)\)
Câu 16:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp
Ba số a, b, c theo thứ tự đó lập thành cấp số cộng thì \(2a = b + c\)
Cách giải
Ba số \(1,\,2\sin x,\,\sin x + 2\) theo thứ tự đó lập thành cấp số cộng \( \Leftrightarrow 2.\left( {2\sin x} \right) = 1 + \left( {\sin x + 2} \right)\)
\( \Rightarrow 4\sin x = 3 + \sin x \Leftrightarrow \sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi ,\,k \in \mathbb{Z}\)
Câu 17:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp
Cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công bội \(q\) thì số hạng thứ n là \({u_n} = {u_1}.{q^{n - 1}}\)
Tổng n số hạng đầu của dãy \({S_n} = \frac{{{u_1}\left( {{q^n} - 1} \right)}}{{q - 1}}\)
Cách giải:
Gọi cấp số nhân \(\left( {{u_n}} \right)\), \({u_n} > 0;\,\forall n\) có số hạng đầu \({u_1}\) và công bội \(q \ne 1\) thì theo đề bài ta có
\(\left\{ \begin{array}{l}{u_5} - {u_4} = 576\\{u_2} - {u_1} = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1}{q^4} - {u_1}{q^3} = 576\\{u_1}q - {u_1} = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1}{q^3}\left( {q - 1} \right) = 576\\{u_1}\left( {q - 1} \right) = 9\end{array} \right.\)
Vì \(q \ne 1\) nên ta có \(\frac{{{u_1}{q^3}\left( {q - 1} \right)}}{{{u_1}\left( {q - 1} \right)}} = \frac{{576}}{9} \Leftrightarrow {q^3} = 64 \Leftrightarrow q = 4\left( {tm} \right)\)
Suy ra \({u_1} = 3\)
Do đó \({S_3} = \frac{{{u_1}\left( {{q^3} - 1} \right)}}{{\left( {q - 1} \right)}} = \frac{{3\left( {{4^3} - 1} \right)}}{{4 - 1}} = 63\)
Câu 18:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp
Cho \(x = 1\) và tính tổng \(S\).
Cách giải:
Ta có: \(P\left( x \right) = {a_{99}}{x^{99}} + {a_{98}}{x^{98}} + ... + {a_1}x + {a_0} = {\left( {5x - 7} \right)^{99}}\)
Dễ thấy \(S = {a_{99}} + {a_{98}} + ... + {a_1} + {a_0} = P\left( 1 \right)\) nên \(S = {\left( {5.1 - 7} \right)^{99}} = {\left( { - 2} \right)^{99}} = - {2^{99}}\)
Câu 19:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Đưa phương trình đã cho về dạng \(\cos a = \cos b \Leftrightarrow \left[ \begin{array}{l}a = b + k2\pi \\a = - b + k2\pi \end{array} \right.\) \(\left( {k \in \mathbb{Z}} \right)\)
Cách giải:
Ta có \[\sin 7x = cos2m \Leftrightarrow cos2m = cos\left( {\frac{\pi }{2} - 7x} \right)\]
\( \Leftrightarrow \left[ \begin{array}{l}2m = \frac{\pi }{2} - 7x + k2\pi \\2m = 7x - \frac{\pi }{2} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{14}} - \frac{m}{7} + \frac{{k2\pi }}{7}\\x = \frac{\pi }{{14}} + \frac{{2m}}{7} - \frac{{k2\pi }}{7}\end{array} \right.\)
Vậy phương trình luôn có nghiệm với mọi \(m\).
Câu 20:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp
Sử dụng công thức tính số hạng thứ n của cấp số cộng \({u_n} = {u_1} + \left( {n - 1} \right)d\)
Cách giải:
Cứ hai cây cách nhau 50m và cây đầu tiên trồng ở đầu đường nên ta coi dãy các cây là một cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 0\), công sai \(d = 50\), cây cuối cùng trồng trên đường là số hạng \({u_n}\) của cấp số cộng.
Có \({u_n} = {u_1} + \left( {n - 1} \right)d \Rightarrow {u_n} = 0 + \left( {n - 1} \right).50 \Leftrightarrow {u_n} = 50\left( {n - 1} \right)\)
Do \(n \in \mathbb{N}*\) nên \({u_n} \vdots 50\). Lại có \({u_n} \le 5270\) nên \({u_n} = 5270\).
Do đó \(5250 = \left( {n - 1} \right).50 \Leftrightarrow n = 106\). Vậy trồng được tất cả 106 cây và dư ra 20m đường.
Chú ý:
Một số em chỉ lấy \(5270:50 = 105\) dư 20 và chọn ngay B là sai vì quên mất cây đầu tiên trồng ngay đầu đường nên phải cộng thêm 1.
Câu 21:
Cho dãy số \(\left( {{u_n}} \right)\) có \({u_1} = 1;\,{u_{n + 1}} = {u_n} + \frac{1}{{{n^2}}},\,\forall n \in \mathbb{N}\). Trong các phát biểu sau, có bao nhiêu phát biểu đúng?
(I) \(\left( {{u_n}} \right)\) là dãy số tăng (II) \(\left( {{u_n}} \right)\) là dãy số bị chặn dưới (III) \({u_2} = 2{u_1}\)
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Cho dãy số \(\left( {{u_n}} \right)\)
+ \(\left( {{u_n}} \right)\) là dãy số tăng khi \({u_n} > {u_{n - 1}}\) \(\left( {\forall n \in \mathbb{N}*} \right)\)
\(\left( {{u_n}} \right)\) là dãy số bị chặn dưới khi tồn tại số \(m\) sao cho \({u_n} \ge m\) \(\left( {\forall n \in \mathbb{N}*} \right)\)
Cách giải:
Ta có \({u_1} = 1;\,{u_{n + 1}} = {u_n} + \frac{1}{{{n^2}}},\,\forall n \in \mathbb{N}\) nên \({u_2} = {u_1} + \frac{1}{{{1^2}}} = 1 + 1 = 2 \Rightarrow {u_2} = 2{u_1}\) nên (III) đúng.
Lại có \({u_{n + 1}} - {u_n} = \frac{1}{{{n^2}}} > 0\) \(\left( {\forall n} \right)\) hay \({u_{n + 1}} > {u_n}\) nên \(\left( {{u_n}} \right)\) là dãy số tăng nên (I) đúng.
Vì \(\left( {{u_n}} \right)\) là dãy số tăng nên ta có \({u_n} \ge {u_1} = 1\) với mọi \(n \in \mathbb{N}*\)
Hay \(\left( {{u_n}} \right)\) là dãy số bị chặn dưới nên (II) đúng.
Câu 22:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp
Tính các số hạng \({u_3},\,{u_4}\) và kết luận.
Cách giải:
Ta có: \({u_3} = 2{u_2} + {u_1} = 2.3 + 2 = 8;\,{u_4} = 2{u_3} + {u_2} = 2.8 + 3 = 19\)
Câu 23:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp
TH1: \(\cos x = 0\)
TH2: \(\cos x \ne 0\)
Chia cả hai vế cho \(co{s^2}x\) đưa về giải phương trình ẩn \(\tan x\).
Sử dụng \(\tan x = m \Leftrightarrow x = \arctan m + k\pi \), \(\left( {k \in \mathbb{Z}} \right)\)
Cách giải:
+ Với \(\cos x = 0\) thay vào phương trình \(2{\sin ^2}x + 3\sin x\cos x + 5{\cos ^2}x = 2\) ta được
\(2{\sin ^2}x = 2 \Leftrightarrow {\sin ^2}x = 1\left( {tm} \right)\) nên \(\cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi \) \(\left( {k \in \mathbb{Z}} \right)\) thỏa mãn phương trình đã cho.
+ Với \(\cos x \ne 0\), ta chia cả hai vế của phương trình cho \({\cos ^2}x \ne 0\) ta được \(2{\tan ^2}x + 3\tan x + 5 = 2.\frac{1}{{co{s^2}x}}\)
\( \Leftrightarrow 2{\tan ^2}x + 3\tan x + 5 = 2\left( {1 + {{\tan }^2}x} \right) \Leftrightarrow 3\tan x = - 3 \Leftrightarrow \tan x = - 1 \Leftrightarrow x = - \frac{\pi }{4} + k\pi \,\left( {k \in \mathbb{Z}} \right)\left( {tm} \right)\)
Vậy họ nghiệm của phương trình là \(x = - \frac{\pi }{4} + k\pi \), \(x = \frac{\pi }{2} + k\pi \) \(\left( {k \in \mathbb{Z}} \right)\)
Câu 24:
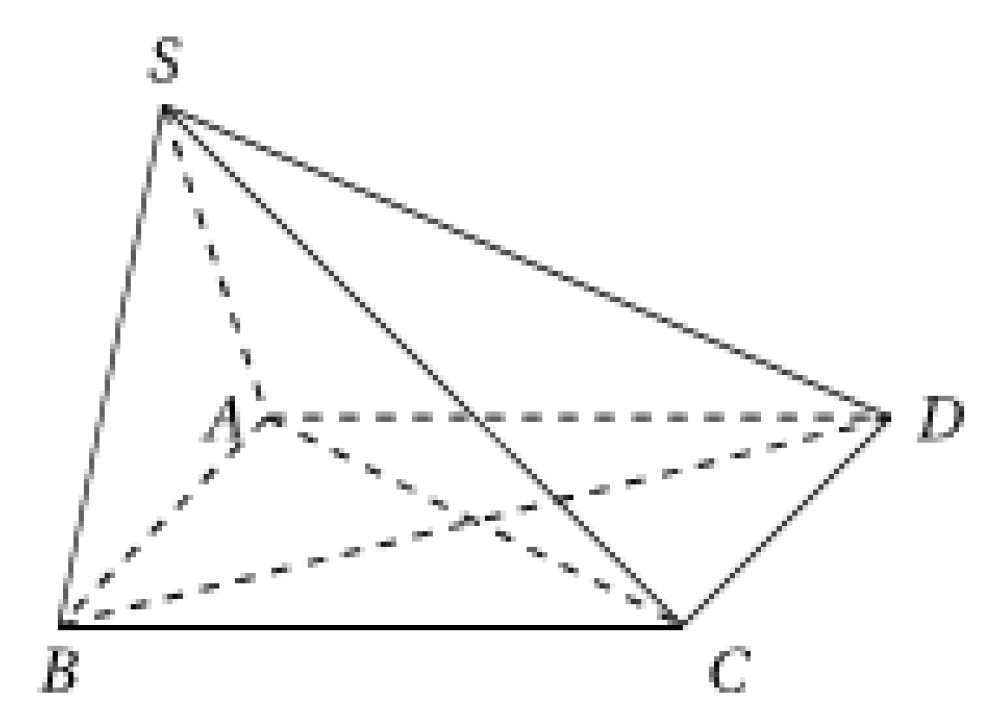
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành (tham khảo hình vẽ). Một mặt phẳng đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD, BD tương ứng tại M, N, E, F, I, J. Có bao nhiêu khẳng định sai trong các khẳng định sau?
I) \(IJ//SB\)
II) \(MF//AC\)
III) Tứ giác \(MNEF\) là hình bình hành.
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp
Dựng hình và nhận xét.
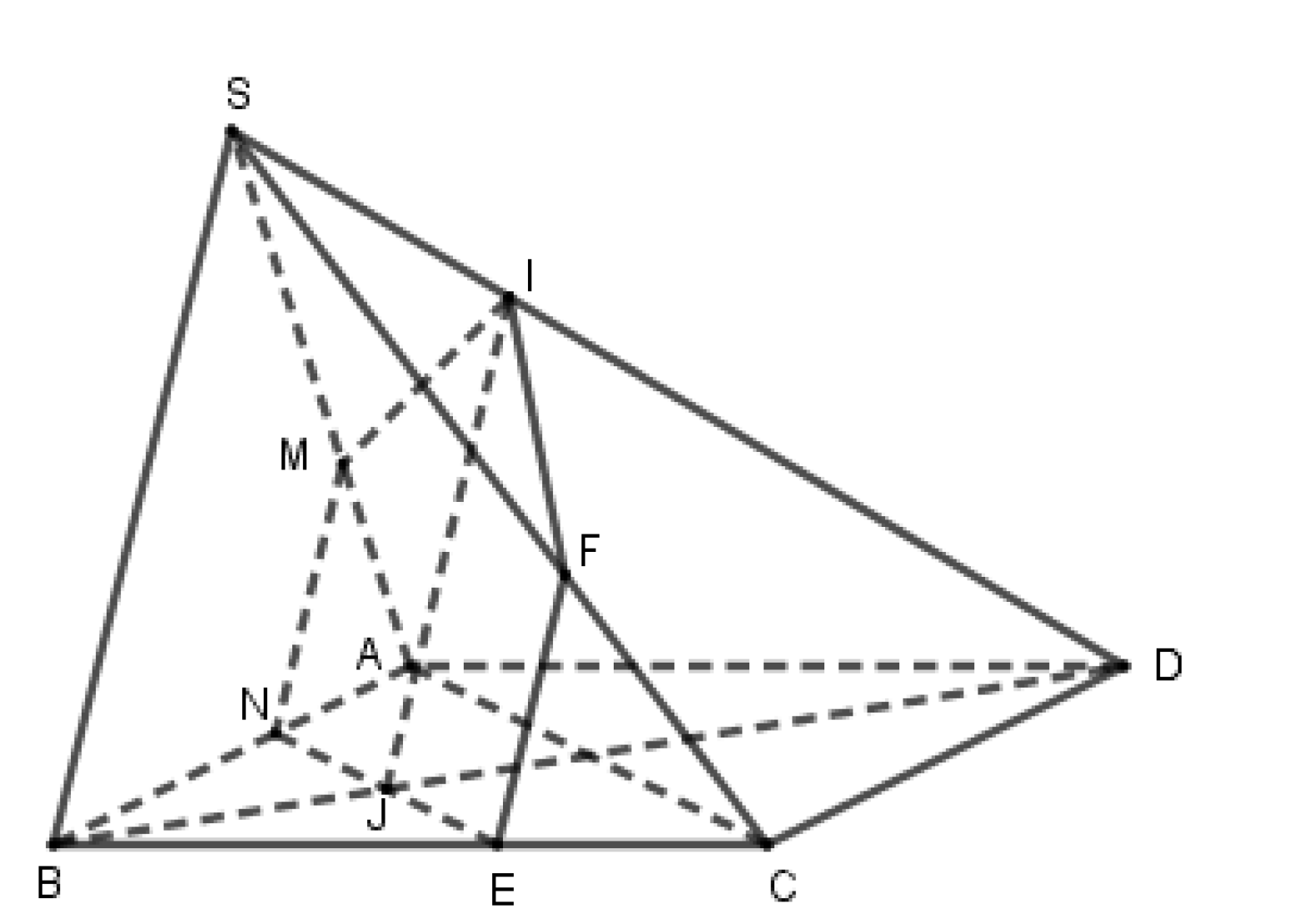
Cách giải:
Lấy \(M\) bất kì thuộc \(SA\).
Trong \(\left( {SAB} \right)\), kẻ \(MN//SB\) \(\left( {N \in AB} \right)\).
Trong \(\left( {ABCD} \right)\), kẻ \(NE//AC\) \(\left( {E \in BC} \right)\).
Trong \(\left( {SBC} \right)\), kẻ \(EF//SB\) \(\left( {F \in SC} \right)\).
Trong \(\left( {ABCD} \right)\), gọi \(NE \cap BD = J\).
Trong \(\left( {SBD} \right)\), kẻ \(JI//SB\) \(\left( {I \in SD} \right)\).
Từ đó ta được mặt phẳng \(\left( {MNEFI} \right)\) thỏa mãn bài toán và các điểm M, N, E, F, J, I.
Dễ thấy, \(SB//JI\) nên (I) đúng.
\(MF//AC\) nên (II) đúng.
Tứ giác \(MNEF\) có \[NE//MF\] (cùng \(//AC\)) và \(FE//MN\) (cùng song song \(SB\) ) nên tứ giác \(MNEF\) là hình bình hành.
Vậy cả ba khẳng định đều đúng.
Câu 25:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d thì \({u_n} = {u_1} + \left( {n - 1} \right)d\) và \({S_n} = n{u_1} + \frac{{n\left( {n - 1} \right)d}}{2}\)
Cách giải:
Ta có \(\left\{ \begin{array}{l}{u_4} = 7{u_1}\\{S_5} = 75\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} + 3d = 7{u_1}\\5{u_1} + \frac{{5.4.d}}{2} = 75\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 6{u_1} + 3d = 0\\5{u_1} + 10d = 75\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} = 3\\d = 6\end{array} \right.\)
Số hạng thứ hai \({u_2} = {u_1} + d = 3 + 6 = 9\).
Câu 26:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng điều kiện hai mặt phẳng song song nhận xét từng đáp án.
Cách giải:
Đáp án A: Đúng.
Đáp án B: Không đủ vì có thể xảy ra trường hợp \(\left( P \right)\) chứa các đường thẳng song song với nhau và song song với \(\left( Q \right)\). Khi đó \(\left( P \right)\) có thể cắt \(\left( Q \right)\) và các đường thẳng song song ở trên đều song song với giao tuyến.
Đáp án C: Đúng.
Đáp án D: Đúng.
Câu 27:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) có tính chất \(u_k^2 = {u_{k - 1}}.{u_{k + 1}}\)
Cách giải:
Vì a, b, c theo thứ tự lập thành một cấp số nhân nên ta có \(ac = {b^2}\)
Mà \(abc = - 27 \Leftrightarrow {b^3} = - 27 \Leftrightarrow b = - 3 \Rightarrow ac = 9\)
Nên \(D = ac - 5b = 9 - 5.\left( { - 3} \right) = 24\).
Câu 28:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
- Sử dụng công thức khai triển nhị thức Newton, khai triển nhị thức đã cho.
- Tìm hệ số của số hạng thứ 12 trong khai triển và kết luận.
Cách giải:
Ta có:
\({\left( {3 - x} \right)^{15}} = \sum\limits_{k = 0}^{15} {C_{15}^k{3^{15 - k}}{{\left( { - x} \right)}^k}} = \sum\limits_{k = 0}^{15} {C_{15}^k{3^{15 - k}}{{\left( { - 1} \right)}^k}{{\left( x \right)}^k}} \)
\( = C_{15}^0 - C_{15}^1{.3^{14}}x + C_{15}^2{.3^{13}}{x^2} - ... + C_{15}^{14}.3{x^{14}} - C_{15}^{15}{x^{15}}\)
Lũy thừa của \(x\) tăng dần ứng với \(k\) tăng dần nên số hạng thứ 12 là \(C_{15}^{11}{3^{15 - 11}}{\left( { - 1} \right)^{11}}{x^{11}}\).
Hệ số của số hạng trên là \(C_{15}^{11}{3^4}{\left( { - 1} \right)^{11}} = - {3^4}C_{15}^{11} = - 110565\).
Câu 29:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Phép vị tự tâm A tỉ số \(k\): \({V_{\left( {I;k} \right)}}\left( M \right) = M' \Leftrightarrow \overrightarrow {IM'} = k\overrightarrow {IM} \)
Cách giải:
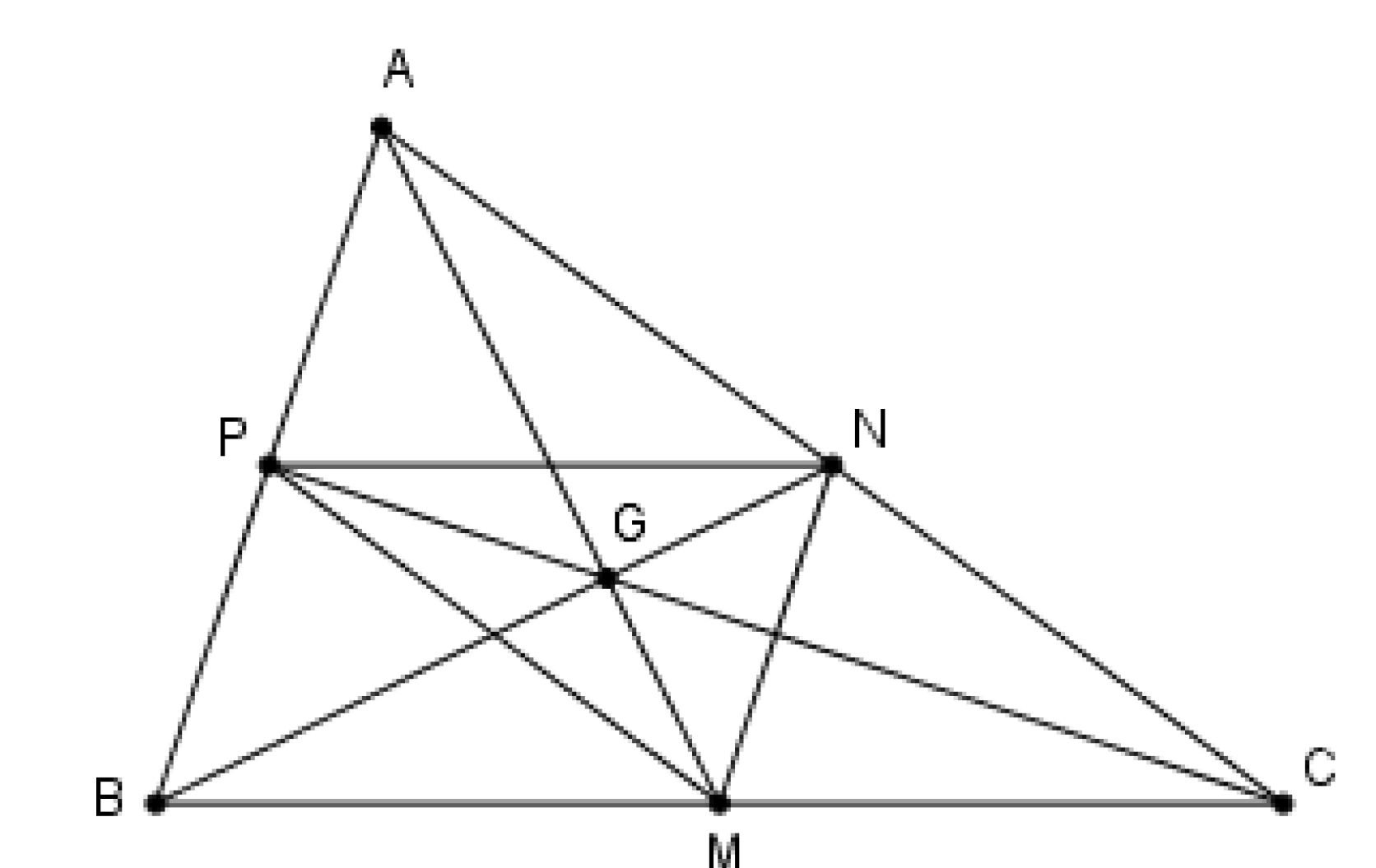
Vì G là trọng tâm tam giác ABC nên \(\frac{{GM}}{{GA}} = \frac{{GN}}{{GB}} = \frac{{GP}}{{GC}} = \frac{1}{2}\) hay
\(\overrightarrow {GM} = - \frac{1}{2}\overrightarrow {GA} ;\,\overrightarrow {GN} = - \frac{1}{2}\overrightarrow {GB} ;\,\overrightarrow {GP} = - \frac{1}{2}\overrightarrow {GC} \)
Xét phép vị tự tâm G tỉ số \( - \frac{1}{2}\)ta có \({V_{\left( {G; - \frac{1}{2}} \right)}}\left( A \right) = M,\,{V_{\left( {G; - \frac{1}{2}} \right)}}\left( B \right) = N,\,{V_{\left( {G; - \frac{1}{2}} \right)}}\left( C \right) = P\) (do
\(\overrightarrow {GM} = - \frac{1}{2}\overrightarrow {GA} ;\,\overrightarrow {GN} = - \frac{1}{2}\overrightarrow {GB} ;\,\overrightarrow {GP} = - \frac{1}{2}\overrightarrow {GC} \) (cmt))
Hay phép vị tự tâm G tỉ số \( - \frac{1}{2}\) biến tam giác ABC thành tam giác MNP.
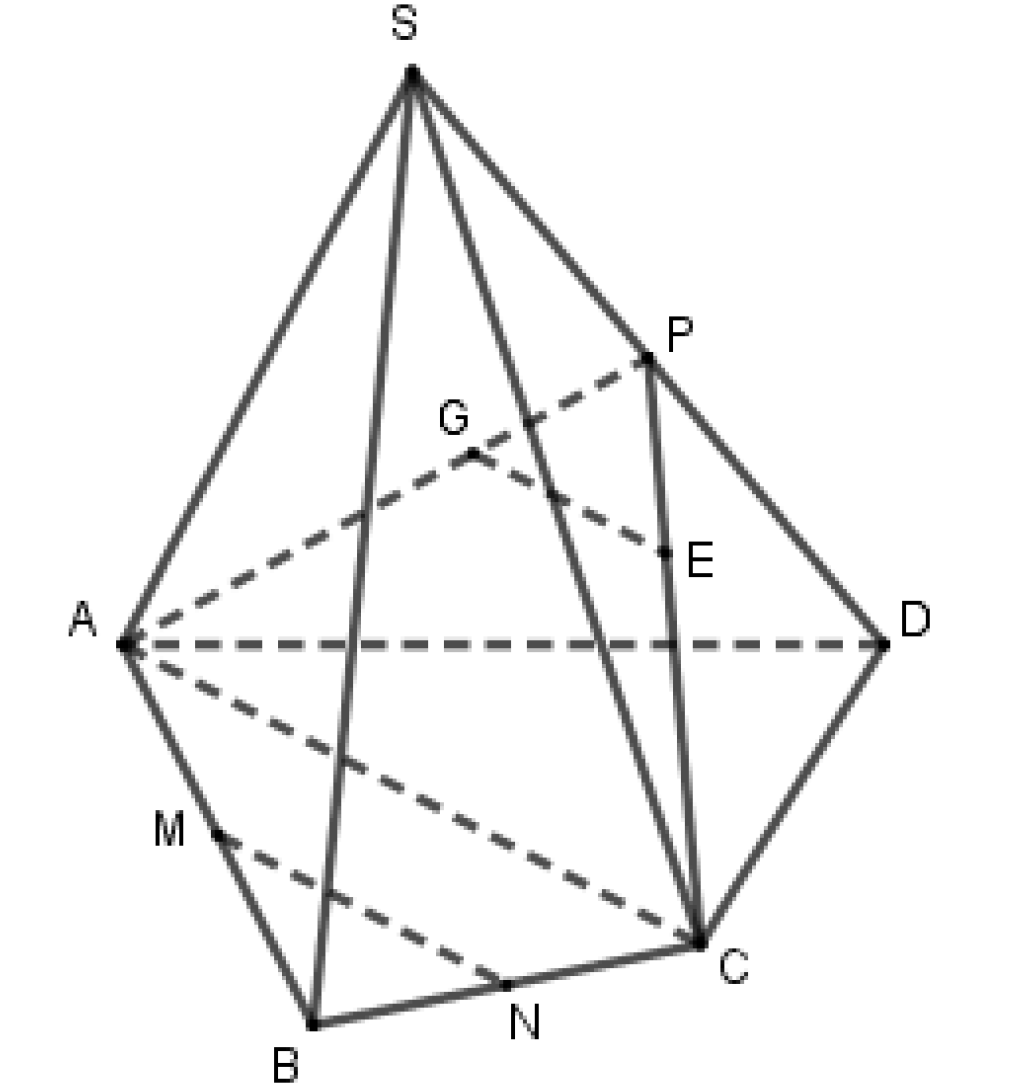
Câu 30:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Dựng hình, nhận xét tính đúng sai của từng đáp án.
Cách giải:
Gọi \(P\) là trung điểm của \(SD\) thì \(AG = \frac{2}{3}AP,\,CE = \frac{2}{3}CP \Rightarrow GE//AC\)
Mà \(MN\) là đường trung bình của tam giác \(ABC\) nên \(MN//AC\).
Vậy \(GE//MN\) (cùng \(//AC\)).
Câu 31:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Cấp số nhân \(\left( {{u_n}} \right)\) với công bội \(q\)và số hạng đầu tiên \({u_1}\) có \({u_n} = {u_{n - 1}}.q\)
\(\left( {{u_n}} \right)\) là dãy số giảm khi \({u_{n + 1}} < {u_n}\), \(\forall n \in \mathbb{N}*\)
Cách giải:
Vì \({u_1} > 0\) nên \(\left( {{u_n}} \right)\) là dãy số giảm thì \(q > 0\) suy ra \({u_n} > 0,\,\forall n\)
Ta có \({u_{n + 1}} = {u_n}q \Leftrightarrow \frac{{{u_{n + 1}}}}{{{u_n}}} = q\) mà \(\left( {{u_n}} \right)\) là dãy số giảm nên \({u_{n + 1}} < {u_n}\), \(\forall n \in \mathbb{N}*\)
Suy ra \(\frac{{{u_{n + 1}}}}{{{u_n}}} < 1 \Rightarrow q < 1\)
Do đó \(0 < q < 1\)
Câu 32:
 Xem đáp án
Xem đáp án
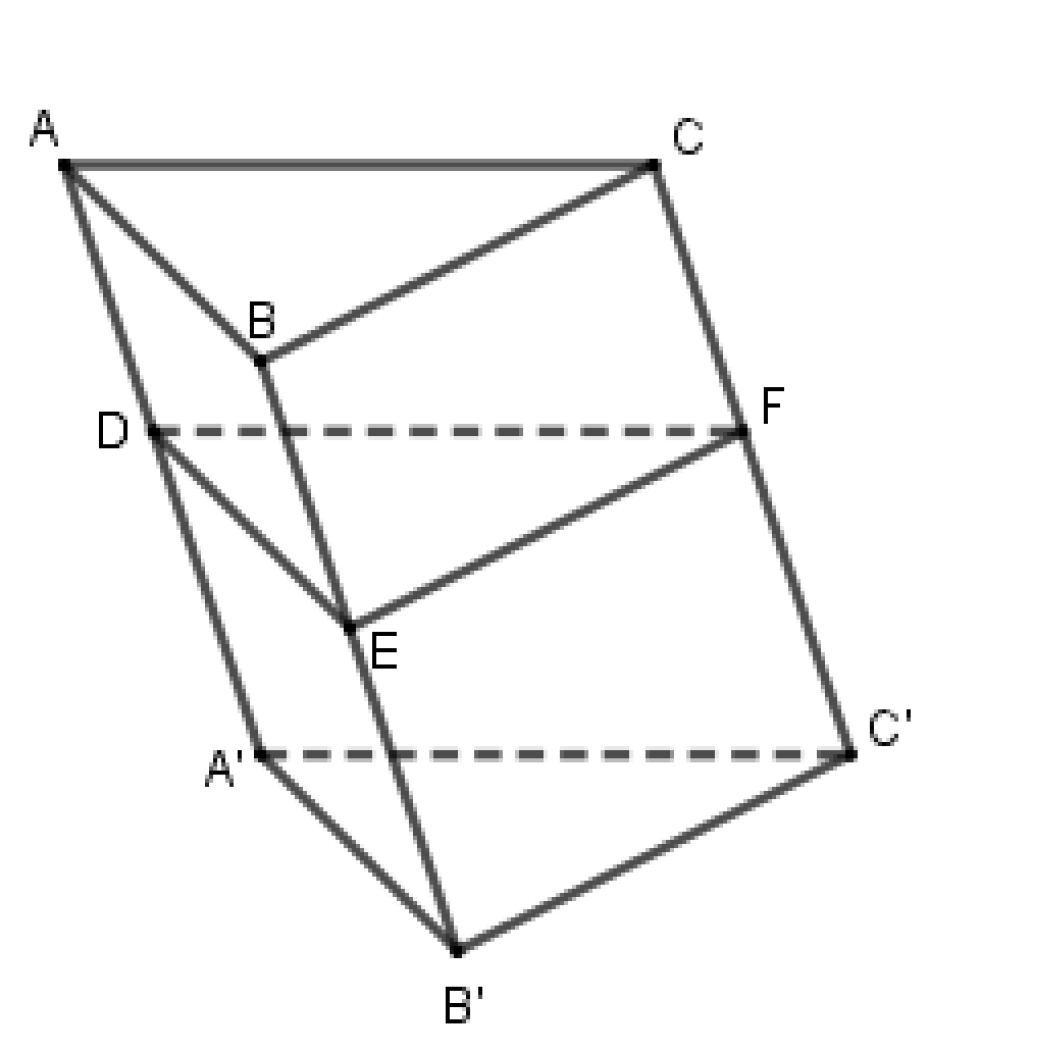
Đáp án D
Phương pháp:
Dựng hình và nhận xét.
Cách giải:
Lăng trụ \(ABC.A'B'C'\) có các cạnh bằng nhau nên tam giác \(ABC\) đều. Khi cắt lăng trụ bởi mặt phẳng song song với đáy ta cũng được tam giác đều \(DFE\).
Câu 33:
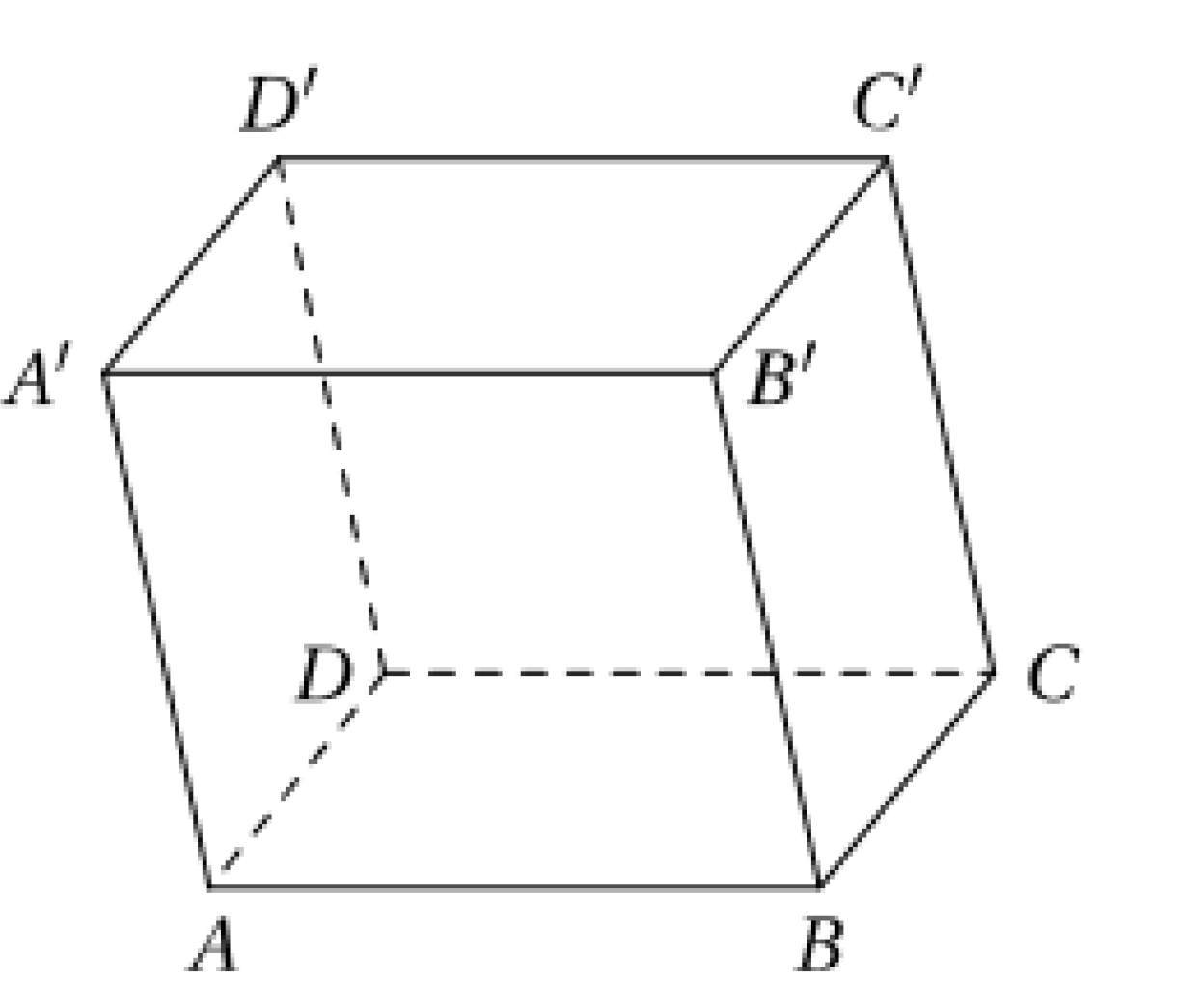
Cho lăng trụ \(ABCD.A'B'C'D'\) có hai đáy là các hình bình hành. Các điểm M, N, P lần lượt là trung điểm của cạnh AD, BC, CC' (tham khảo hình vẽ). Xét các khẳng định sau:
I) Mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(A'D'\)
II) Mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(DD'\) tại trung điểm của \(DD'\)
III) Mặt phẳng \(\left( {MNP} \right)\) song song với mặt phẳng \(\left( {ABC'D'} \right)\)
Trong các khẳng định trên, số khẳng định đúng là
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Sử dụng cách tìm giao điểm của đường thẳng và mặt phẳng
Chứng minh hai mặt phẳng \(\left( P \right),\,\left( Q \right)\) song song dựa vào \(\left\{ \begin{array}{l}a//b\\c//d\\a,\,c \subset \left( P \right),\,a \cap c\\b,d \subset \left( Q \right),\,b \cap d\end{array} \right. \Rightarrow \left( P \right)//\left( Q \right)\)
Cách giải
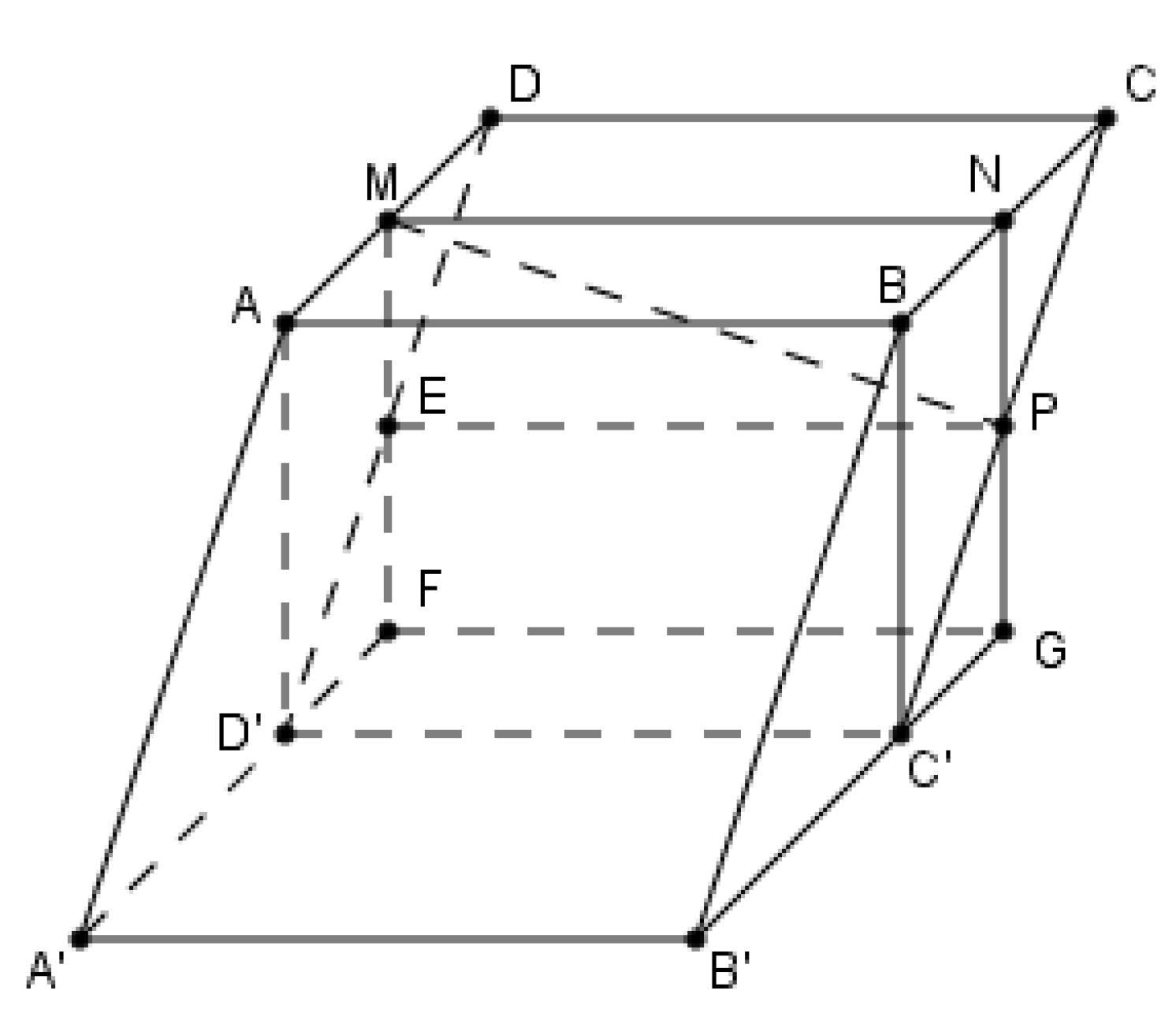
+ Lấy \(E\) là trung điểm \(DD' \Rightarrow EP//CD//MN\) suy ra \(\left( {MNP} \right) \equiv \left( {MNPE} \right)\)
Do đó \(\left( {MNP} \right) \cap DD' = E\) với \(E\) là trung điểm \(DD'\) nên II) đúng.
+ Trong \(\left( {ADD'A'} \right)\) có \(ME\) cắt tia \(A'D'\) tại \(F\) suy ra \(\left( {MNPE} \right) \cap A'D' = \left\{ F \right\}\)
Ta có \(AMFD'\) là hình bình hành (do \(MF//AD';\,AM//D'F\)) nên \(AM = D'F = \frac{1}{2}A'D' \Rightarrow A'F = \frac{3}{2}A'D\)
Nên \(F\) không thuộc cạnh \(A'D'\) do đó I) sai.
+ Ta có \(ME//AD'\) (do \(ME\) là đường trung bình \(\Delta DAD'\)) và \(MN//AB\) nên \(\left( {MNP} \right)//\left( {ABC'D'} \right)\) do đó III) đúng.
Câu 34:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Đếm số các số bằng cách sử dụng quy tắc nhân.
Cách giải:
Gọi số tự nhiên thỏa mãn bài toán là \(\overline {abc} \) với \(a,b,c \in \left\{ {0;2;4;6;8;9} \right\},\,a \ne 0\)
Ta có: \(a \ne 0\) nên có 5 cách chọn \(a\).
Có 6 cách chọn \(b\) và 6 cách chọn \(c\).
Vậy có \(5.6.6 = 180\) số.
Câu 35:
Trong các mệnh đề sau, có bao nhiêu mệnh đề đúng?
I) Hàm số \(y = x + {\mathop{\rm sinx}\nolimits} \) tuần hoàn với chu kì \(T = 2\pi \)
II) Hàm số \(y = x\cos x\) là hàm số lẻ
III) Hàm số \(y = \tan x\) đồng biến trên từng khoảng xác định
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Hàm số \(y = f\left( x \right)\) tuần hoàn với chu kì \(T \Leftrightarrow \left\{ \begin{array}{l}x \in D \Rightarrow x + T \in D\\f\left( x \right) = f\left( {x + T} \right)\end{array} \right.\)
Hàm số \(y = f\left( x \right)\) là hàm số lẻ \( \Leftrightarrow \left\{ \begin{array}{l}x \in D \Rightarrow - x \in D\\f\left( { - x} \right) = - f\left( x \right)\end{array} \right.\)
Cách giải:
A. Sai vì \(f\left( {x + 2\pi } \right) = x + 2\pi + \sin \left( {x + 2\pi } \right) = x + \sin x + 2\pi \ne f\left( x \right)\)
B. Đúng vì \(\left\{ \begin{array}{l}x \in \mathbb{R} \Rightarrow - x \in \mathbb{R}\\f\left( { - x} \right) = - x.cos\left( { - x} \right) = - x\cos x = - f\left( x \right)\end{array} \right.\)
C. Đúng vì hàm số \(y = \tan x\) đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\,\frac{\pi }{2} + k\pi } \right)\)
Câu 36:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Sử dụng công thức tính số hạng tổng quát của cấp số nhân \({u_n} = {u_1}{q^{n - 1}}\)
Lập hệ phương trình ẩn \(q,\,{u_1}\) và giải phương trình.
Cách giải:
Ta có: \({u_5} = 15,\,{u_8} = - 1875 \Rightarrow \left\{ \begin{array}{l}{u_1}{q^4} = 15\\{u_1}{q^7} = - 1875\end{array} \right. \Rightarrow {q^3} = - 125 \Rightarrow q = - 5\)
Câu 37:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Dựng các đường thẳng qua \(M\) và song song với các cạnh của tam giác \(SAB\) ta được mặt phẳng \(\left( \alpha \right)\) cần dựng
Từ đó ta xác định thiết diện của hình chóp cắt bởi mặt phẳng \(\left( \alpha \right)\)
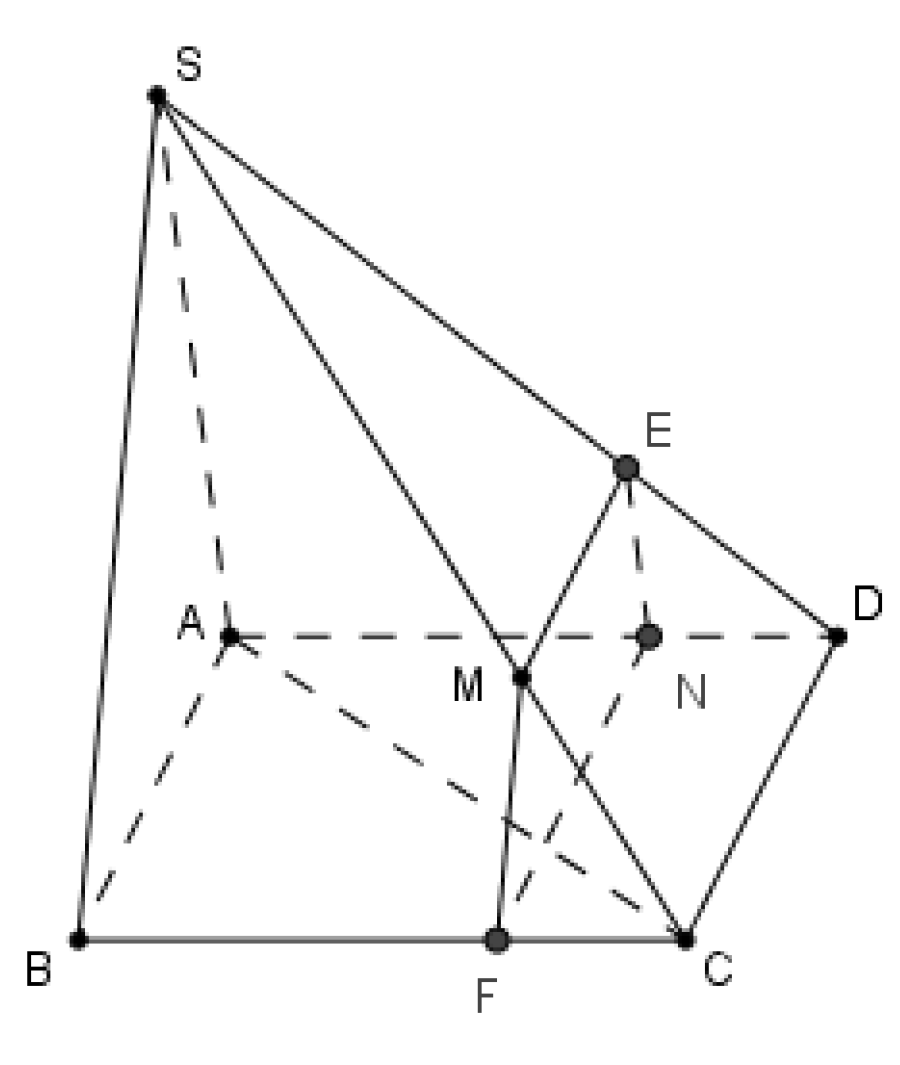
Cách giải:
+ Trong mặt phẳng \(\left( {SBC} \right)\) kẻ \(MF//SB\) \(\left( {F \in BC} \right)\)
+ Trong mặt phẳng \(\left( {ABCD} \right)\) kẻ \(FN//BA\) \(\left( {N \in AD} \right)\)
Từ đó ta có \(\left( {MNF} \right)//\left( {SAB} \right)\)
Trong \(\left( {SCD} \right)\) kẻ \(ME//CD\) \(\left( {E \in SD} \right) \Rightarrow ME//CD//FN//AB\) hay \(\left( {MNF} \right) \equiv \left( {MFNE} \right)\)
Suy ra \(\left( \alpha \right) \equiv \left( {MFNE} \right)\)
Ta có \(\left\{ \begin{array}{l}\left( \alpha \right) \cap \left( {SBC} \right) = MF\\\left( \alpha \right) \cap \left( {SDC} \right) = ME\\\left( \alpha \right) \cap \left( {SAD} \right) = NE\\\left( \alpha \right) \cap \left( {ABCD} \right) = NF\end{array} \right.\) nên thiết diện cắt bởi \(\left( \alpha \right)\)là tứ giác \(MENF\)
Mà \(ME//FN \Rightarrow MENF\) là hình thang.
Câu 38:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Đếm số trận đấu của mỗi đội trong giải đấu, từ đó suy ra số trận đấu trong giải.
Cách giải:
Cứ mỗi đội trong giải đấu phải đấu với 13 đội còn lại nên có 13 trận đấu.
Vậy 14 đội có \(14.13 = 182\) trận đấu.
Câu 39:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng tính chất hình bình hành, tính chất đường trung bình của tam giác
Sử dụng cách tìm giao tuyến của hai mặt phẳng, tìm giao điểm của đường thẳng và mặt phẳng.
Cách giải:
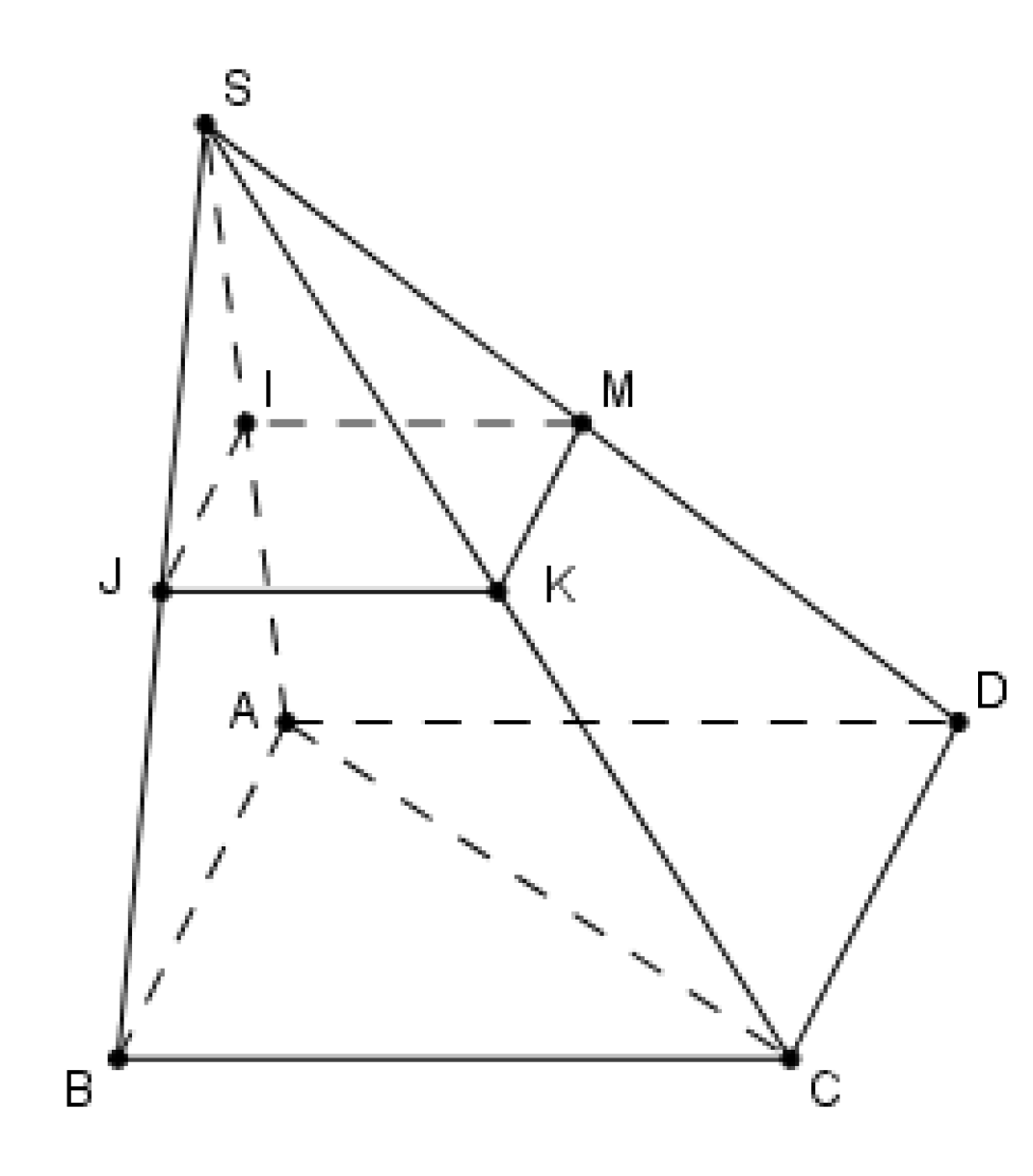
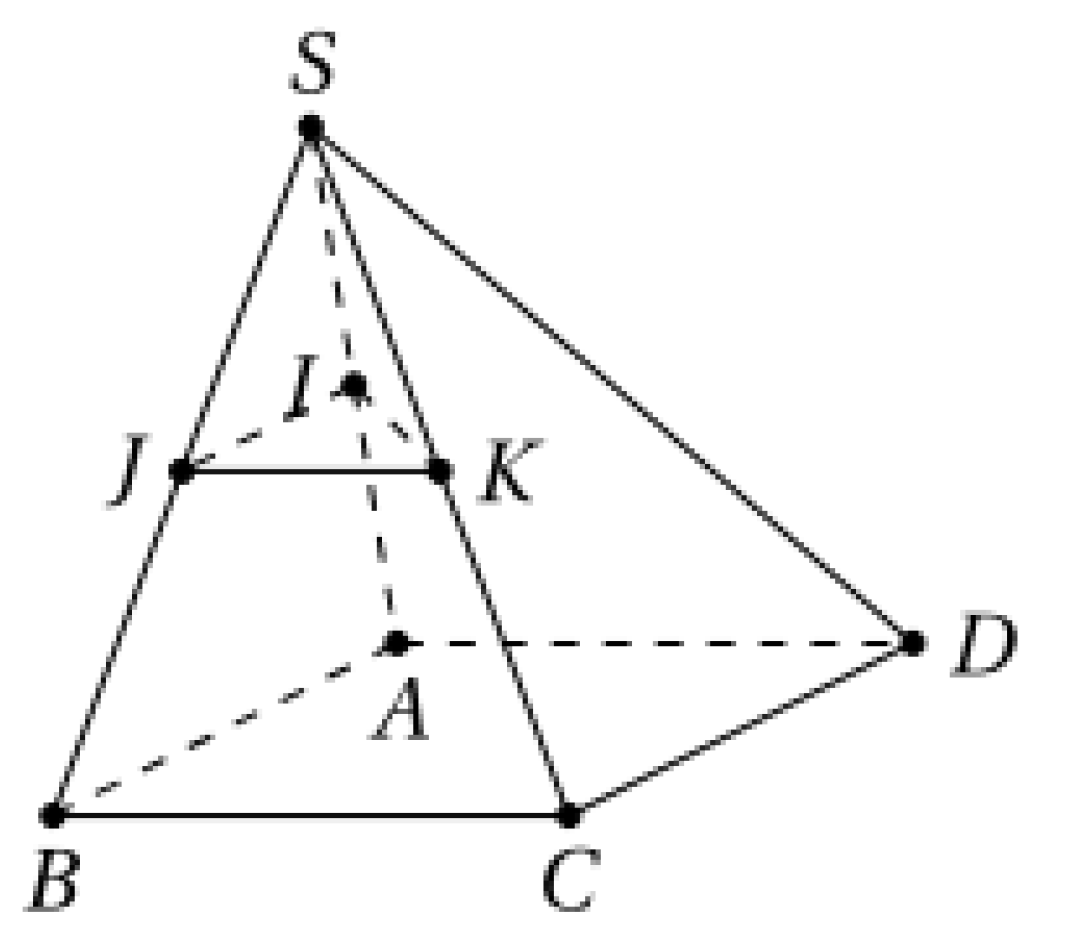
Vì \(ABCD\) là hình bình hành nên \(AB//CD\), lại có \(IJ//AB\) (do \(IJ\) là đường trung bình của tam giác \(SAB\)) nên \(IJ//CD\) hay A đúng.
Lấy \(M\) là trung điểm của \(SD \Rightarrow IJKM\) là hình bình hành nên \(\left( {IJK} \right) \cap SD = \left\{ M \right\}\), do đó B sai.
Vì \(\left\{ \begin{array}{l}IJ//AB\\JK//BC\end{array} \right. \Rightarrow \left( {IJK} \right)//\left( {ACD} \right)\) nên \(\left( {IJK} \right) \cap \left( {ACD} \right) = \emptyset \), do đó C đúng.
+ \(IK//AC\) do \(IK\) là đường trung bình tam giác \(SAC\) nên D đúng.
Câu 40:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Sử dụng phương pháp phần bù, đếm số cách xếp mà hai bạn nữ đứng cạnh nhau, từ đó suy ra kết quả.
Cách giải:
Số cách xếp 5 bạn trong một hàng ngang là \(5! = 120\) cách.
Ta đếm số cách xếp 5 bạn, trong đó 2 bạn nữ đứng cạnh nhau.
Gom 2 bạn nữ thành một cặp thì có \(2! = 2\) cách đổi chỗ hai bạn này.
Nhóm này cùng với 3 bạn nam còn lại tạo thành 4 bạn thì có \(4! = 24\) cách xếp chỗ.
Do đó có \(2.24 = 48\) cách xếp 5 bạn sao cho 2 bạn nữ đứng cạnh nhau.
Vậy có \(120 - 48 = 72\) cách xếp chỗ mà hai bạn nữ không đứng cạnh nhau.
Câu 41:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
- Tính số phần tử của không gian mẫu (số cách chọn 4 trong 9 thẻ và đem ra sắp xếp)
- Tìm số cách lấy ra bốn thẻ và xếp cạnh nhau theo thứ tự từ trái sang phải để được một số chẵn.
- Tính xác suất theo công thức \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\)
Cách giải:
+ Số phần tử của không gian mẫu \(n\left( \Omega \right) = A_9^4\)
+ Gọi A là biến cố: Lấy ra bốn thẻ và xếp cạnh nhau theo thứ tự từ trái sang phải để được một số chẵn
Gọi 4 thẻ được lấy ra, sắp xếp cạnh nhau là \(abcd\)và là một số chẵn.
+ \(d \in \left\{ {2;4;6;8} \right\}\) nên \(d\) có 4 cách chọn
+ a có 8 cách chọn, \(b\) có 7 cách chọn và \(c\) có 6 cách chọn
Nên \(n\left( A \right) = 8.7.6.4 = 1344\)
Xác suất cần tìm là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{1344}}{{A_9^4}} = \frac{4}{9}\)
Câu 42:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Chứng minh \(MN\) cắt mặt phẳng \(\left( {ACB'} \right)\) dẫn đến không có mặt phẳng cần tìm.
Cách giải:
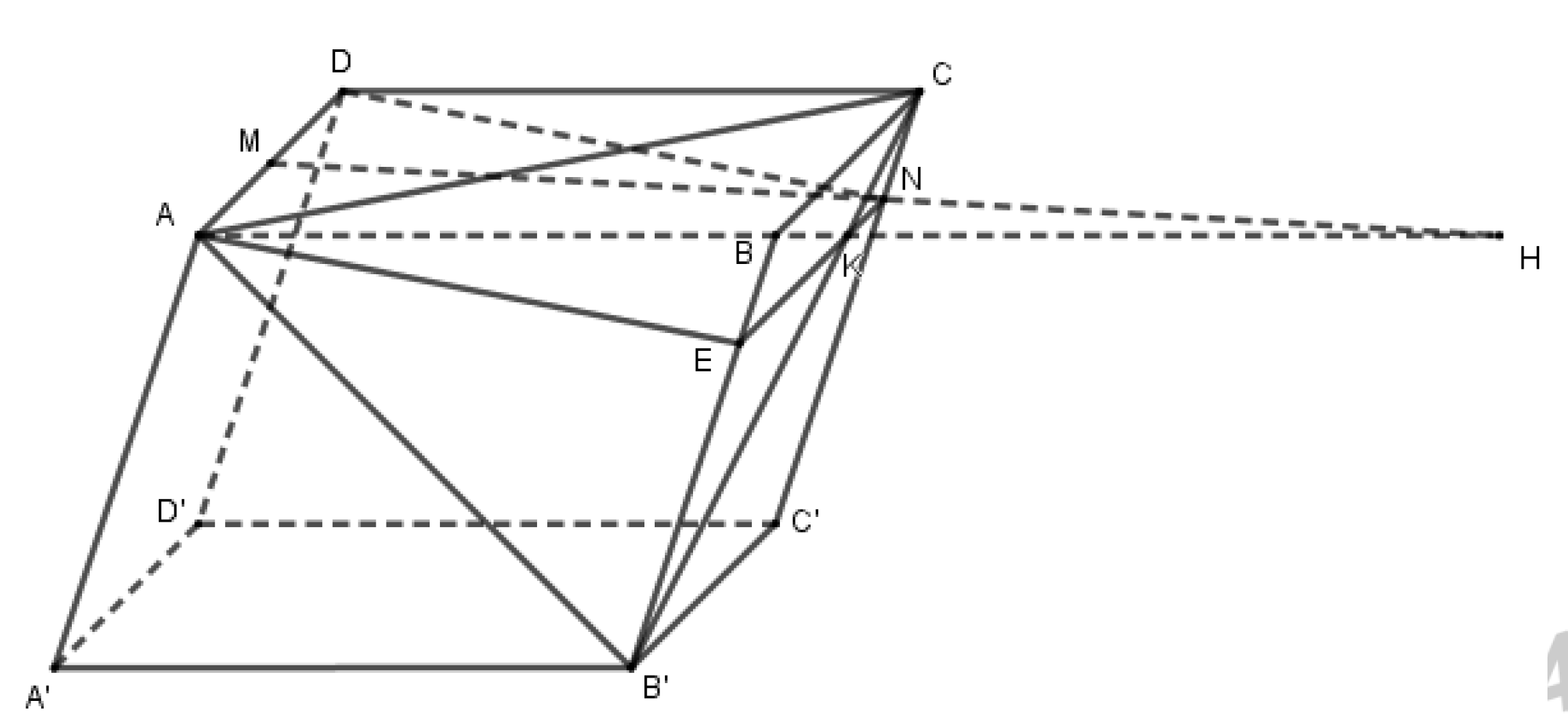
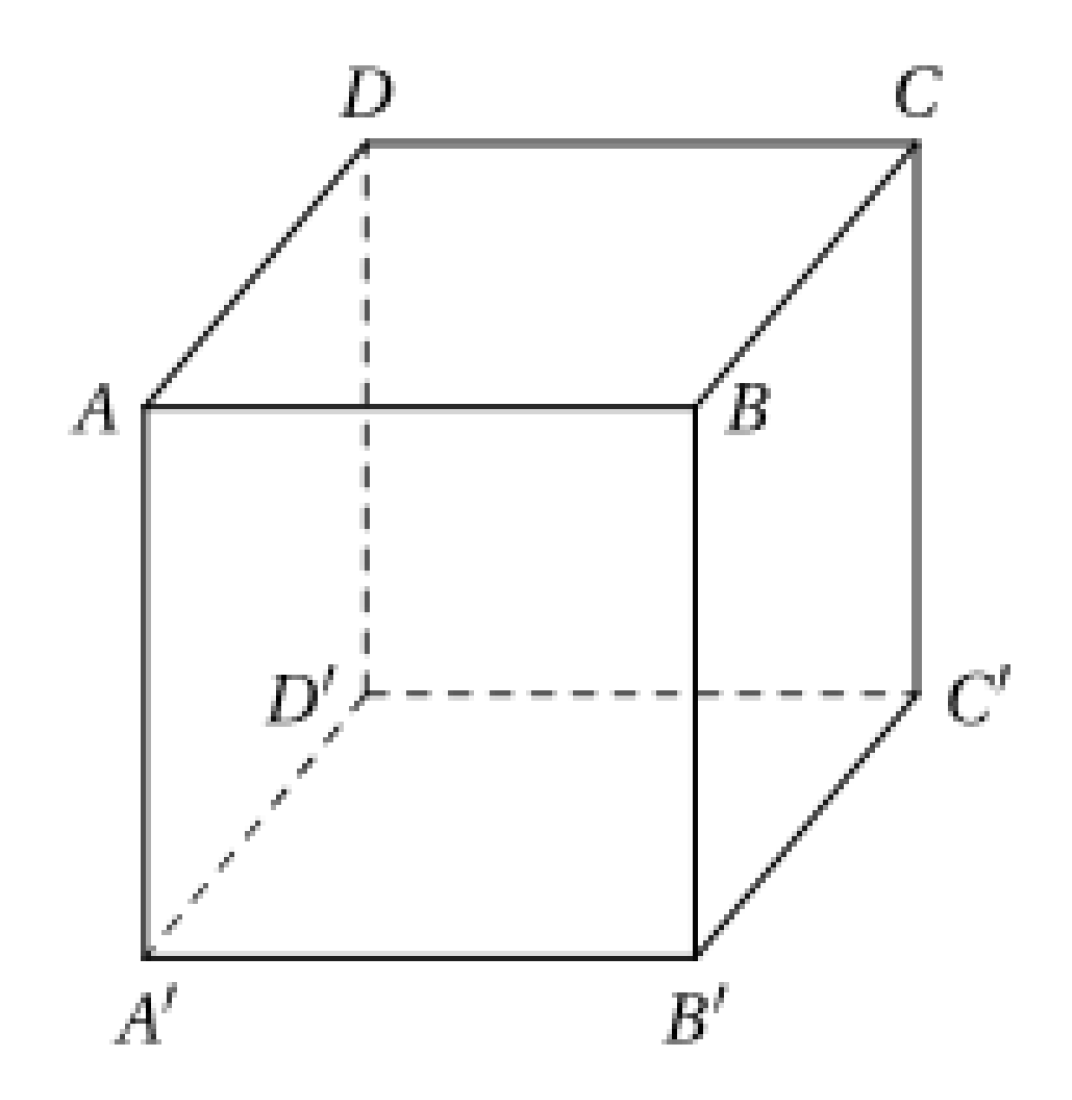
Qua N kẻ \(NE//BC\) \(\left( {E \in BB'} \right)\), \(NE \cap B'C = K\).
Dễ thấy \(NE//BC//AD\) nên các điểm A, M, N, E cùng thuộc mặt phẳng \(\left( {ADNE} \right)\).
Lại có \(K = NE \cap CB' \Rightarrow K \in CB' \subset \left( {ACB'} \right) \Rightarrow AK \subset \left( {ACB'} \right)\)
Trong mặt phẳng \(\left( {ADMN} \right)\) gọi \(H = MN \cap AK \Rightarrow \left\{ \begin{array}{l}H \in MN\\H \in AK \subset \left( {ACB'} \right)\end{array} \right. \Rightarrow H = MN \cap \left( {ACB'} \right)\)
Do đó không có mặt phẳng nào chứa \(MN\) và song song \(\left( {ACB'} \right)\) .
Vậy không có thiết diện cần tìm.
Câu 43:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
+ Dựng mặt phẳng \(\left( \alpha \right)\) dựa vào mối quan hệ song song với \(BB',\,AC\)
+ Từ đó tính tỉ số \(\frac{{TB}}{{TC}}\)
Cách giải:
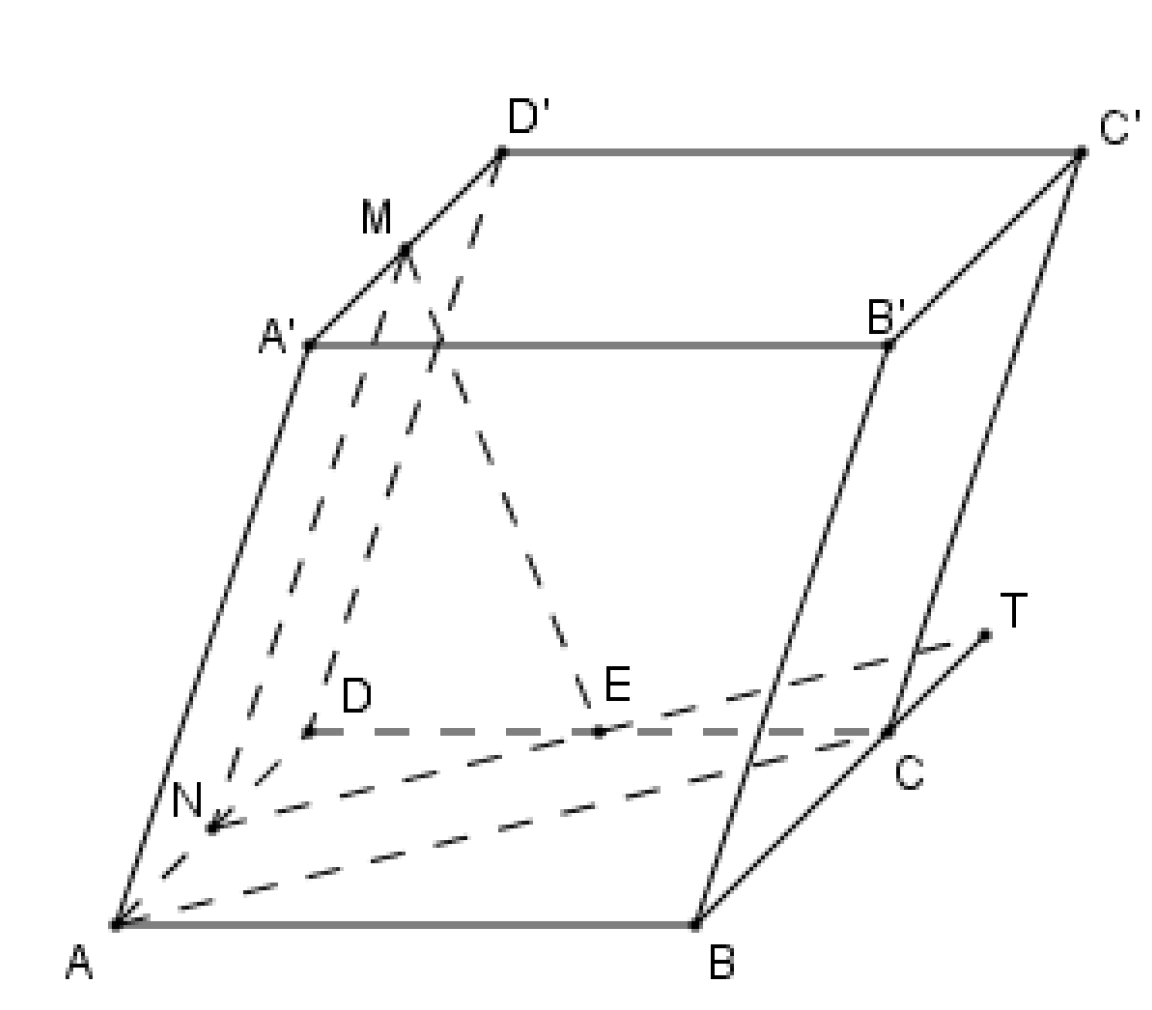
Gọi \(N,E\) lần lượt là trung điểm của \(AD,DC\)
Ta có \(MN//AA'//BB'\) và \(NE//AC\) (do \(NE\) là đường trung bình của tam giác \(DAC\))
Suy ra \(\left( \alpha \right) \equiv \left( {MNE} \right)\)
Trong \(\left( {ABCD} \right)\), kéo dài \(NE\) cắt \(BC\) tại \(T\). Suy ra \(ANTC\)là hình bình hành (do \(AN//TC;\,NT//AC\))
Do đó \(TC = AN = \frac{1}{2}AD = \frac{1}{2}BC\)
Ta có \(\left( {MNE} \right) \cap BC = \left\{ T \right\}\) nên \(\frac{{TB}}{{TC}} = \frac{{\frac{3}{2}BC}}{{\frac{1}{2}BC}} = 3\)
Câu 44:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
- Tính số phần tử của không gian mẫu (số cách chọn 6 trong 19 quả cầu).
- Liệt kê và đếm số cách lấy mà số quả cầu xanh bằng số quả cầu đỏ.
- Tính xác suất theo công thức \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\)
Cách giải:
Số cách chọn 6 trong 19 quả cầu là \(n\left( \Omega \right) = C_{19}^6\)
Gọi A là biến cố: Lấy được 6 quả cầu đủ ba loại sao cho số quả cầu xanh bằng số quả cầu đỏ. Ta đếm số cách chọn 6 quả cầu đủ ba loại sao cho số quả cầu xanh bằng số quả cầu đỏ.
+ TH1: 1 quả xanh, 1 quả đỏ và 4 quả vàng có \(C_9^1.C_3^1.C_7^4\) cách chọn.
+ TH2: 2 quả xanh, 2 quả đỏ và 2 quả vàng có \(C_9^2.C_3^2.C_7^2\) cách chọn.
Suy ra \(n\left( A \right) = C_9^1.C_3^1.C_7^4 + C_9^2.C_3^2.C_7^2\)
Vậy xác suất là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_9^1.C_3^1.C_7^4 + C_9^2.C_3^2.C_7^2}}{{C_{19}^6}} = \frac{9}{{76}}\)
Câu 45:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
+ Dựng mặt phẳng \(\left( \alpha \right)\) theo mối quan hệ song song với \(AC,\,BD\)
+ Tìm thiết diện của mặt phẳng \(\left( \alpha \right)\) với hình chóp
+ Dựa vào điều kiện hình thoi và định lý Ta-lét để tính toán.
Cách giải:
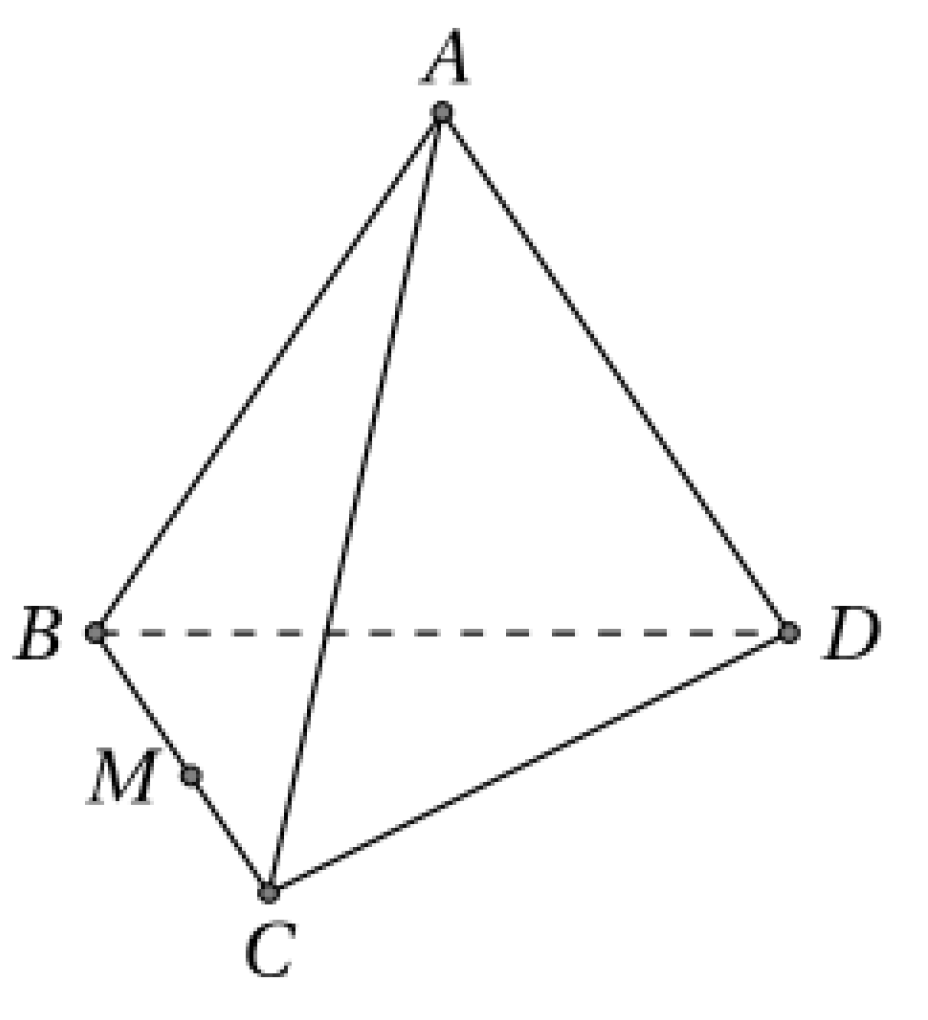
Trong \(\left( {ABC} \right)\) kẻ \(MH//AC\) \(\left( {H \in AB} \right)\)
Trong \(\left( {BCD} \right)\) kẻ \(ME//DB\) \(\left( {E \in DC} \right)\)
Trong \(\left( {ABD} \right)\) kẻ \(HN//AD\) \(\left( {N \in AD} \right)\)
Suy ra \(HN//ME\).
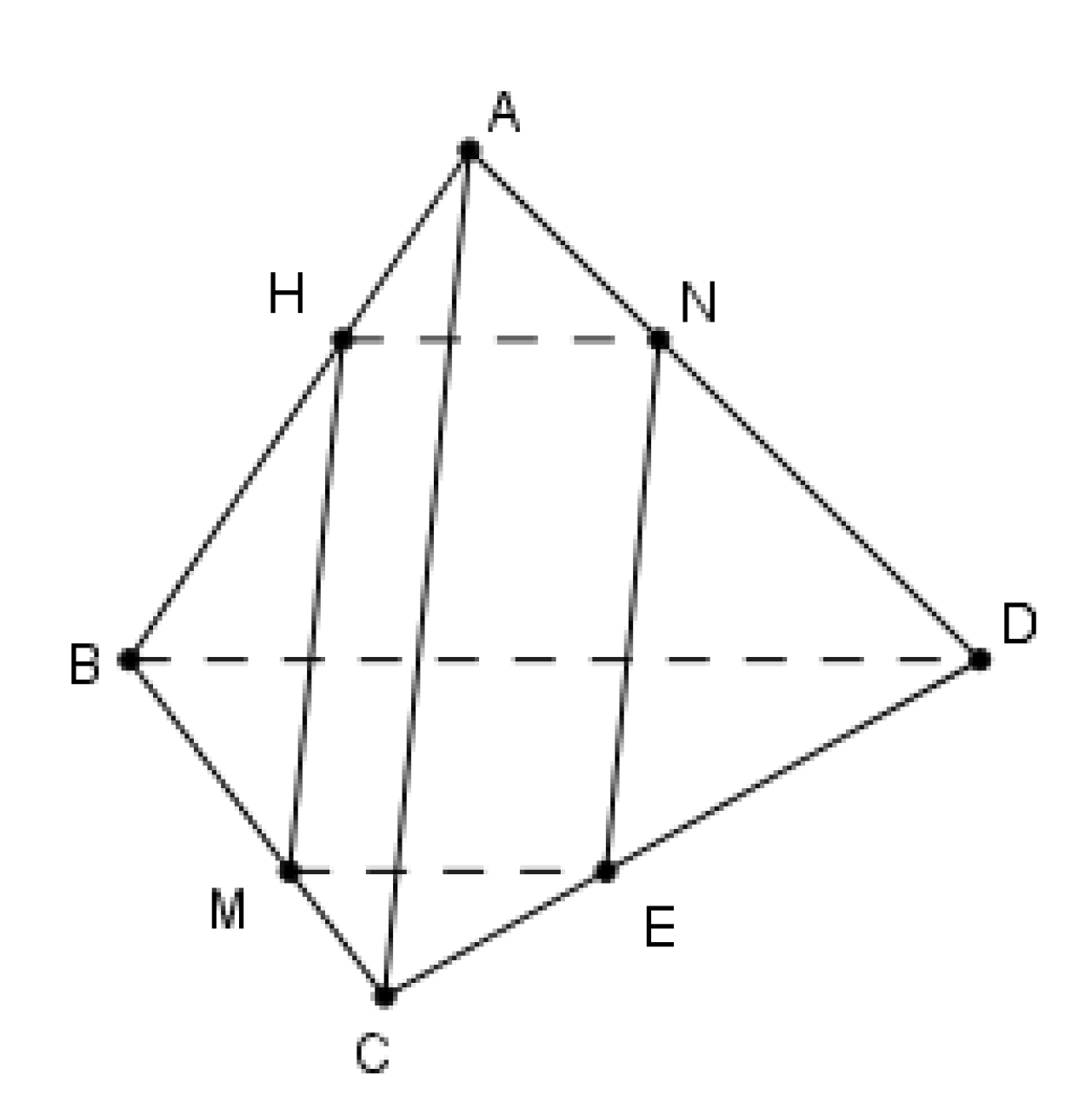
Theo định lý Ta-lét ta có: \(\frac{{HN}}{{BD}} = \frac{{AH}}{{AB}} = \frac{{MC}}{{BC}} = \frac{{ME}}{{BD}} \Rightarrow HN = ME\)
Từ đó \[MENH\] là hình bình hành.
Ta có \(\left( \alpha \right) \equiv \left( {MENH} \right)\) và \(\left\{ \begin{array}{l}\left( {MENH} \right) \cap \left( {ABC} \right) = MH\\\left( {MENH} \right) \cap \left( {BCD} \right) = ME\\\left( {MENH} \right) \cap \left( {ABD} \right) = NH\\\left( {MENH} \right) \cap \left( {ACD} \right) = NE\end{array} \right.\) nên thiết diện cần tìm là hình bình hành \[MENH\]
Để \[MENH\] là hình thoi thì \(MH = NE\)
+ Giả sử \(MC = a\,\left( {0 < a < 9} \right) \Rightarrow MB = 9 - a\)
Theo định lý Ta-lét ta có \(\frac{{ME}}{{BD}} = \frac{{MC}}{{BC}} \Leftrightarrow \frac{{ME}}{3} = \frac{a}{9} \Leftrightarrow ME = \frac{a}{3}\)
Theo định lý Ta-lét ta có \(\frac{{MH}}{{AC}} = \frac{{BM}}{{BC}} \Leftrightarrow \frac{{MH}}{6} = \frac{{9 - a}}{9} \Leftrightarrow MH = \frac{{18 - 2a}}{3}\)
Mà \(ME = MH \Leftrightarrow \frac{a}{3} = \frac{{18 - 2a}}{3} \Leftrightarrow a = 18 - 2a \Leftrightarrow a = 6\)
Suy ra \({M_0}C = 6;\,{M_0}B = 3 \Rightarrow {M_0}B.{M_0}C = 6.3 = 18\).
Câu 46:
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \({u_1} = 6\) và \({u_{n + 1}} = \frac{1}{9}\left( {u_n^2 - {u_n} + 25} \right)\) với mọi số tự nhiên \(n \ge 1\). Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
I) \(\left( {{u_n}} \right)\) là dãy số không tăng, không giảm.
II) \(\frac{1}{{{u_1} + 4}} = \frac{1}{{{u_1} - 5}} - \frac{1}{{{u_2} - 5}}\)
III) \(\frac{1}{{{u_1} + 4}} + \frac{1}{{{u_2} + 4}} + ... + \frac{1}{{{u_{2018}} + 4}} = 1 - \frac{1}{{{u_{2019}} - 5}}\)
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Xét tính đúng sai của từng mệnh đề bằng cách sử dụng định nghĩa dãy số tăng, giảm, tính các số hạng đầu của dãy, nhận xét quy luật,...
Cách giải:
Mệnh đề (I): Xét \({u_{n + 1}} - {u_n} = \frac{1}{9}\left( {u_n^2 - {u_n} + 25} \right) - {u_n} = \frac{{u_n^2 - 10{u_n} + 25}}{9} = \frac{{{{\left( {{u_n} - 5} \right)}^2}}}{9} \ge 0,\,\forall {u_n}\)
\( \Rightarrow {u_{n + 1}} \ge {u_n},\,\forall n\) hay \(\left( {{u_n}} \right)\) là dãy số tăng \( \Rightarrow \) (I) sai.
Mệnh đề (II): Ta có: \({u_1} = 6,\,{u_2} = \frac{{55}}{9}\)
\( \Rightarrow \frac{1}{{{u_1} + 4}} = \frac{1}{{6 + 4}} = \frac{1}{{10}}\) và \(\frac{1}{{{u_1} - 5}} - \frac{1}{{{u_2} - 5}} = \frac{1}{{6 - 5}} - \frac{1}{{\frac{{55}}{9} - 5}} = \frac{1}{{10}}\)
\( \Rightarrow \frac{1}{{{u_1} + 4}} = \frac{1}{{{u_1} - 5}} - \frac{1}{{{u_2} - 5}}\) hay (II) đúng.
Mệnh đề (III): Ta có: \({u_{n + 1}} - 5 = \frac{1}{9}\left( {u_n^2 - {u_n} + 25} \right) - 5 = \frac{{u_n^2 - {u_n} - 20}}{9} = \frac{{\left( {{u_n} - 5} \right)\left( {{u_n} + 4} \right)}}{9}\)
\( \Rightarrow \frac{1}{{{u_{n + 1}} - 5}} = \frac{9}{{\left( {{u_n} - 5} \right)\left( {{u_n} + 4} \right)}} = \frac{1}{{{u_n} - 5}} - \frac{1}{{{u_n} + 4}} \Rightarrow \frac{1}{{{u_n} + 4}} = \frac{1}{{{u_n} - 5}} - \frac{1}{{{u_{n + 1}} - 5}}\)
\( \Rightarrow \frac{1}{{{u_1} + 4}} + \frac{1}{{{u_2} + 4}} + ... + \frac{1}{{{u_{2018}} + 4}} = \frac{1}{{{u_1} - 5}} - \frac{1}{{{u_2} - 5}} + \frac{1}{{{u_2} - 5}} - \frac{1}{{{u_3} - 5}} + ... + \frac{1}{{{u_{2018}} - 5}} - \frac{1}{{{u_{2019}} - 5}}\)
\( = \frac{1}{{{u_1} - 5}} - \frac{1}{{{u_{2019}} - 5}} = \frac{1}{{6 - 5}} - \frac{1}{{{u_{2019}} - 5}} = 1 - \frac{1}{{{u_{2019}} - 5}}\)
Nên (III) đúng.
Vậy (I) sai và (II), (III) đúng.
Câu 47:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Cấp số cộng có số hạng đầu \({u_1}\) và công sai \(d\) thì có tổng \(n\)số hạng đầu là \({S_n} = \frac{{\left( {{u_1} + {u_n}} \right)n}}{2}\)
Cách giải:
Ta có số các số hạng của dãy là \(\frac{{3n + 1 - 1}}{3} + 1 = n + 1\) số
Nên \(1 + 4 + 7 + .. + \left( {3n + 1} \right) = 4187 \Leftrightarrow \frac{{\left( {1 + 3n + 1} \right)\left( {n + 1} \right)}}{2} = 4187 \Leftrightarrow \left( {3n + 2} \right)\left( {n + 1} \right) - 8374 = 0\)
\( \Leftrightarrow 3{n^2} + 5n - 8372 = 0 \Leftrightarrow \left[ \begin{array}{l}n = 52\left( {tm} \right)\\n = - \frac{{161}}{3}\left( {ktm} \right)\end{array} \right.\)
Vậy \(n = 52\).
Câu 48:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Liệt kê và đếm số cách chọn 2 bạn thỏa mãn có 1 bạn nam và 1 bạn nữ tổ khác.
Các trường hợp: nam tổ I và nữ hai tổ còn lại; nam tổ II và nữ hai tổ còn lại; nam tổ III và nữ hai tổ còn lại
Cách giải:
Số cách chọn 1 bạn nam tổ I và 1 bạn nữ hai tổ còn lại là \(C_3^1.C_9^1 = 27\) cách chọn.
Số cách chọn 1 bạn nam tổ II và 1 bạn nữ hai tổ còn lại là \(C_5^1.C_{11}^1 = 55\) cách chọn.
Số cách chọn 1 bạn nam tổ III và 1 bạn nữ hai tổ còn lại là \(C_6^1.C_{12}^1 = 72\) cách chọn.
Vậy có \(27 + 55 + 72 = 154\) cách chọn.
Câu 49:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
+ Tính xác suất để người chơi thua 1 lần
+ Tính xác suất \({P_1}\) để người chơi thua 3 lần
+ Tính xác suất để người chơi có ít nhất 1 lần thắng: \(P = 1 - {P_1}\)
Cách giải:
+ Không gian mẫu: \(n\left( \Omega \right) = 6.6.6 = 216\)
+ Để người chơi thua thì
- Chỉ có 1 con súc sắc có mặt hơn 4 chấm: \(C_3^1.2.C_4^1C_4^1\)
- Cả ba con súc sắc đều có mặt không lớn hơn 4 chấm: \(C_4^1C_4^1C_4^1\)
Xác suất để người đó chơi thua 1 lần là \({P_1} = \frac{{C_3^1.2.4.4 + C_4^1C_4^1C_4^1}}{{216}} = \frac{{20}}{{27}}\)
Xác suất để người đó chơi thua 3 cả lần chơi là \({\left( {{P_1}} \right)^3} = {\left( {\frac{{20}}{{27}}} \right)^3}\)
Xác suất để người đó thắng ít nhất 1 lần trong 3 lần chơi là \(P = 1 - {\left( {\frac{{20}}{{27}}} \right)^3} = \frac{{11683}}{{19683}}\)
Câu 50:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Giải phương trình và biểu diễn trên đường tròn đơn vị.
Cách giải:
Ta có:
\(cos2x - \sin x \Leftrightarrow cos2x = \sin x \Leftrightarrow cos2x = cos\left( {\frac{\pi }{2} - x} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{2} - x + k2\pi \\2x = - \frac{\pi }{2} + x + k2\pi \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{\pi }{6} + \frac{{k2\pi }}{3}\\x = - \frac{\pi }{2} + k2\pi \end{array} \right.,\,k \in \mathbb{Z}\)
Biểu diễn trên đường tròn đơn vị:
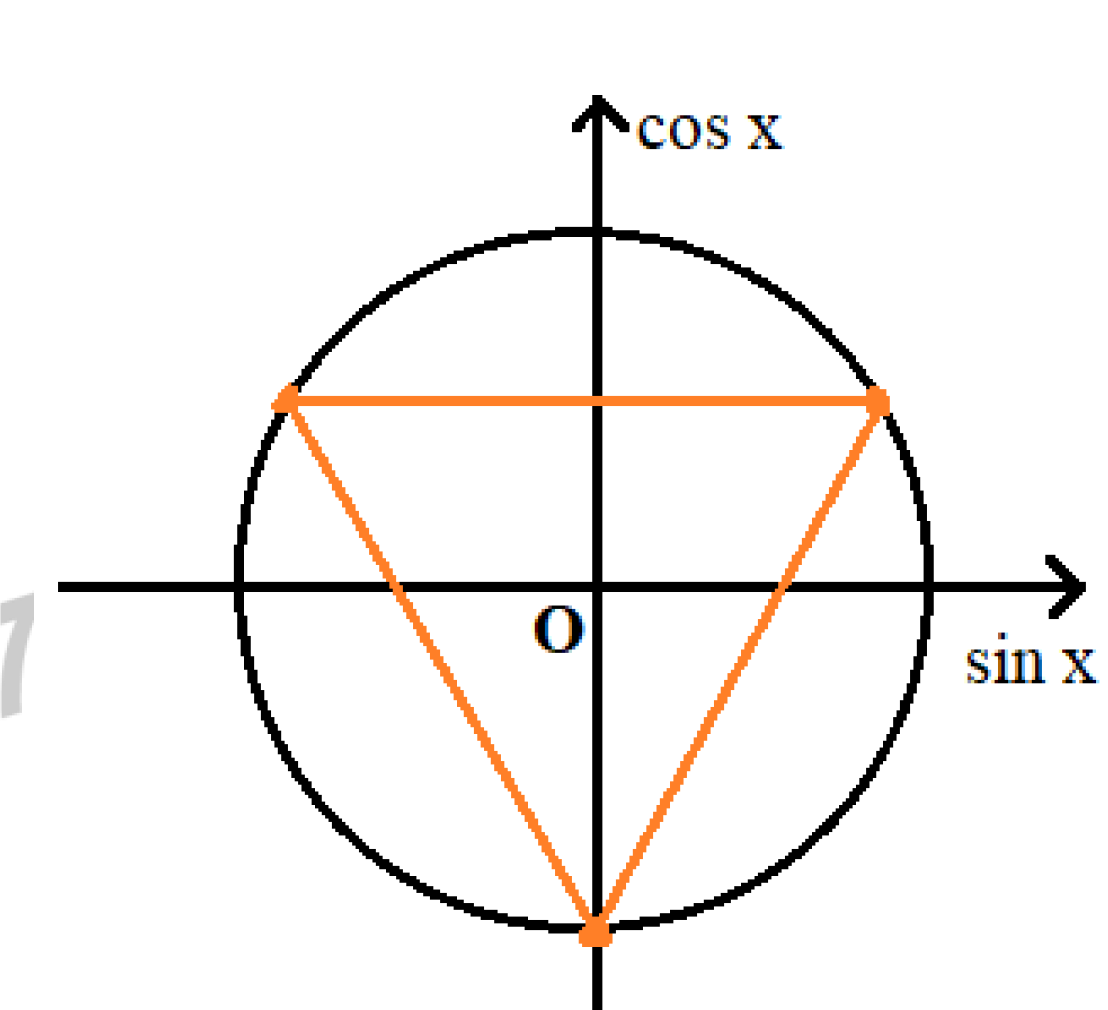
Từ hình vẽ ta thấy có tất cả 3 điểm biểu diễn nghiệm của phương trình trên đường tròn đơn vị.
