 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Phương pháp:
Sử dụng tính chất hình bình hành, tính chất đường trung bình của tam giác
Sử dụng cách tìm giao tuyến của hai mặt phẳng, tìm giao điểm của đường thẳng và mặt phẳng.
Cách giải:
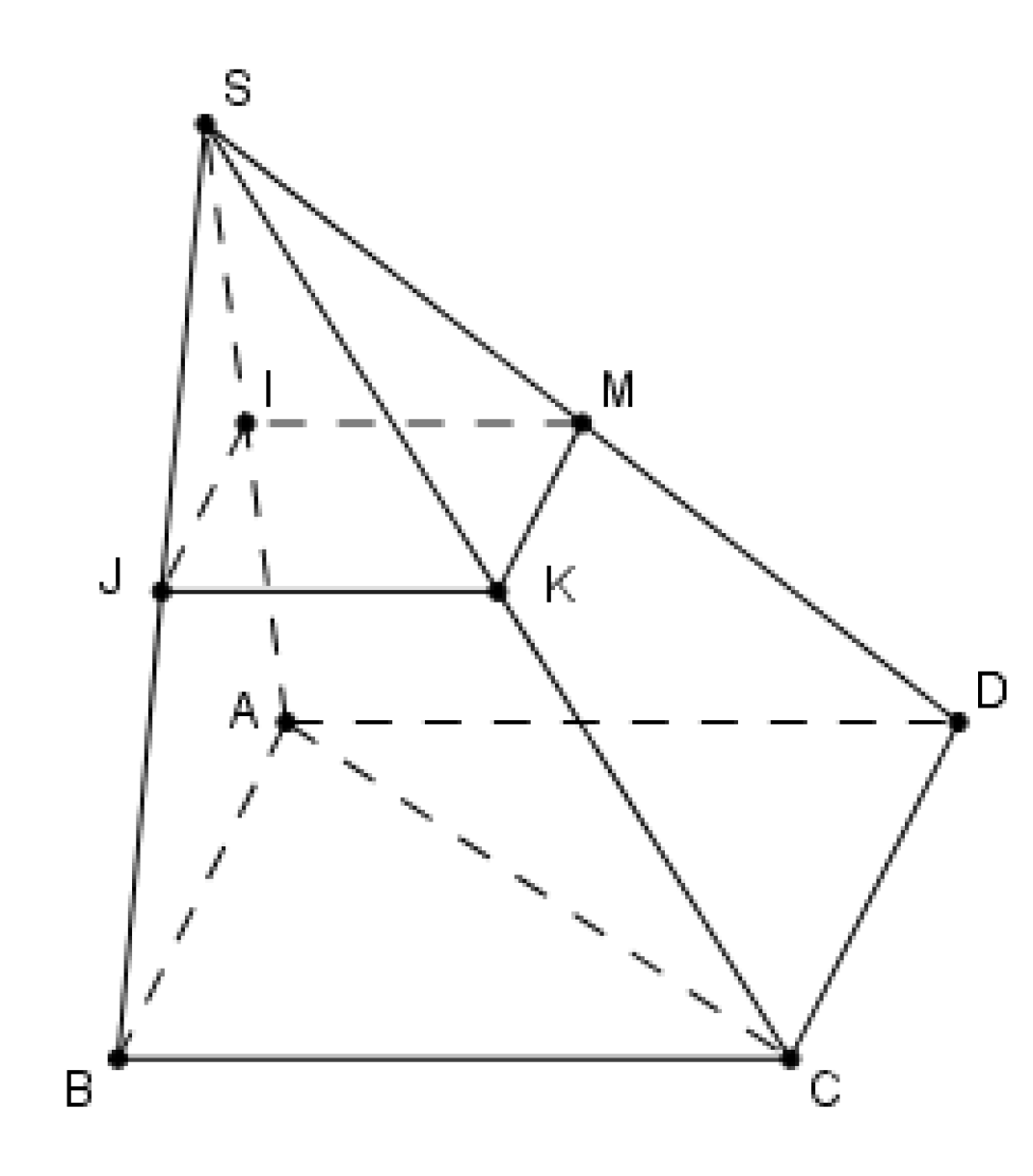
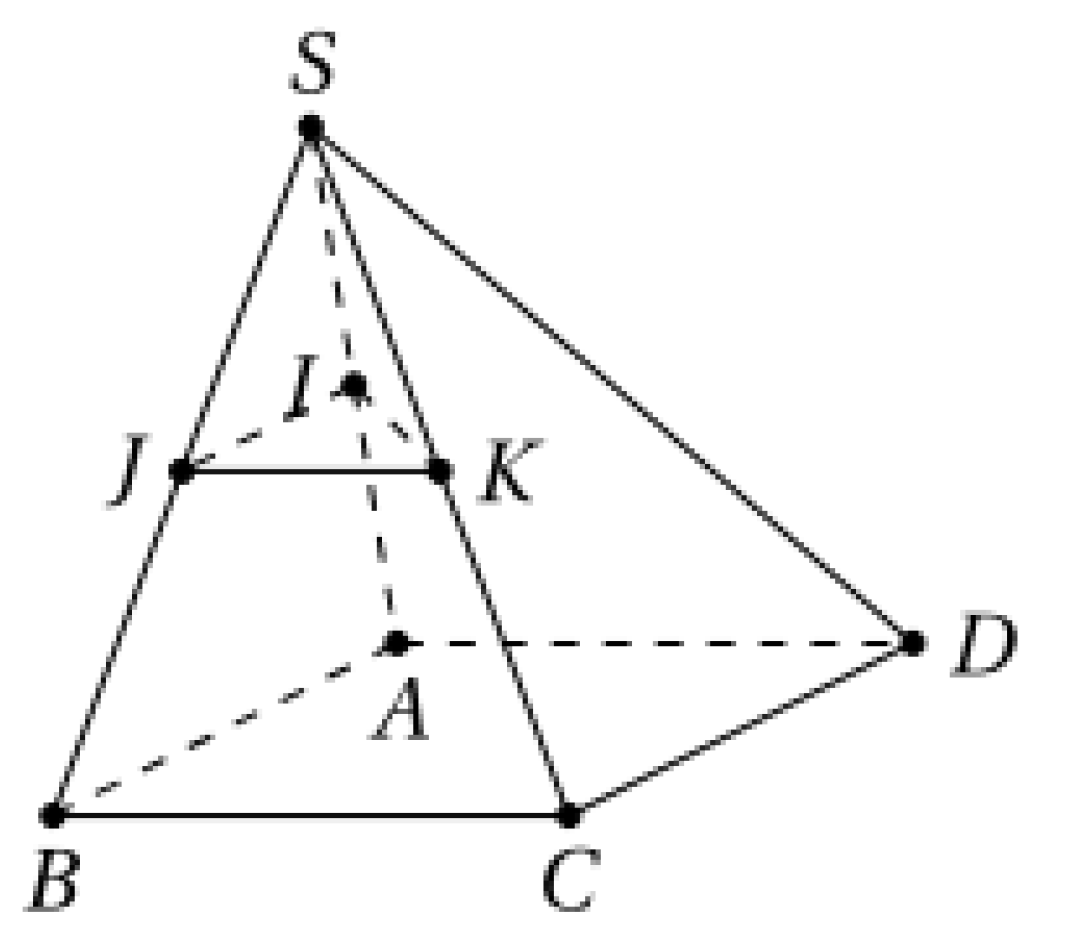
Vì \(ABCD\) là hình bình hành nên \(AB//CD\), lại có \(IJ//AB\) (do \(IJ\) là đường trung bình của tam giác \(SAB\)) nên \(IJ//CD\) hay A đúng.
Lấy \(M\) là trung điểm của \(SD \Rightarrow IJKM\) là hình bình hành nên \(\left( {IJK} \right) \cap SD = \left\{ M \right\}\), do đó B sai.
Vì \(\left\{ \begin{array}{l}IJ//AB\\JK//BC\end{array} \right. \Rightarrow \left( {IJK} \right)//\left( {ACD} \right)\) nên \(\left( {IJK} \right) \cap \left( {ACD} \right) = \emptyset \), do đó C đúng.
+ \(IK//AC\) do \(IK\) là đường trung bình tam giác \(SAC\) nên D đúng.
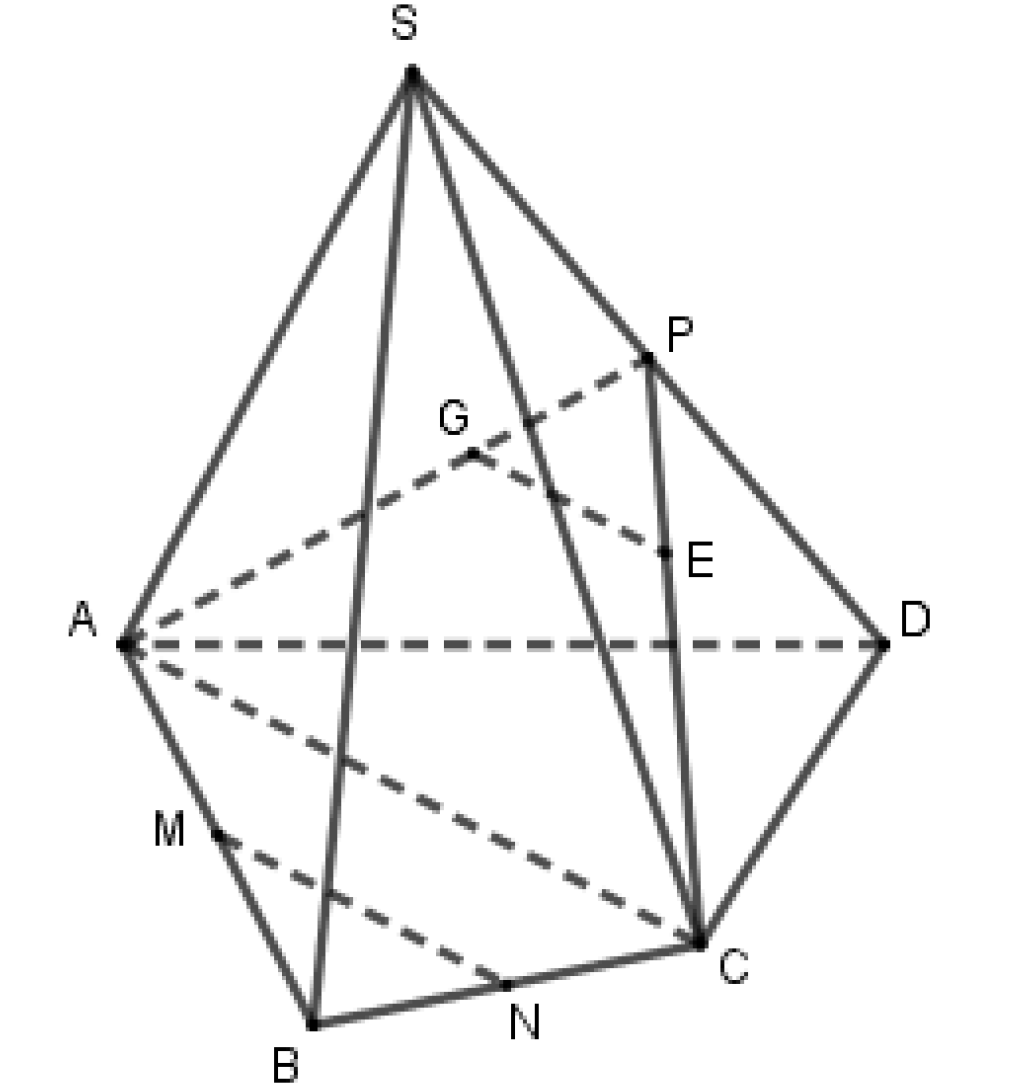
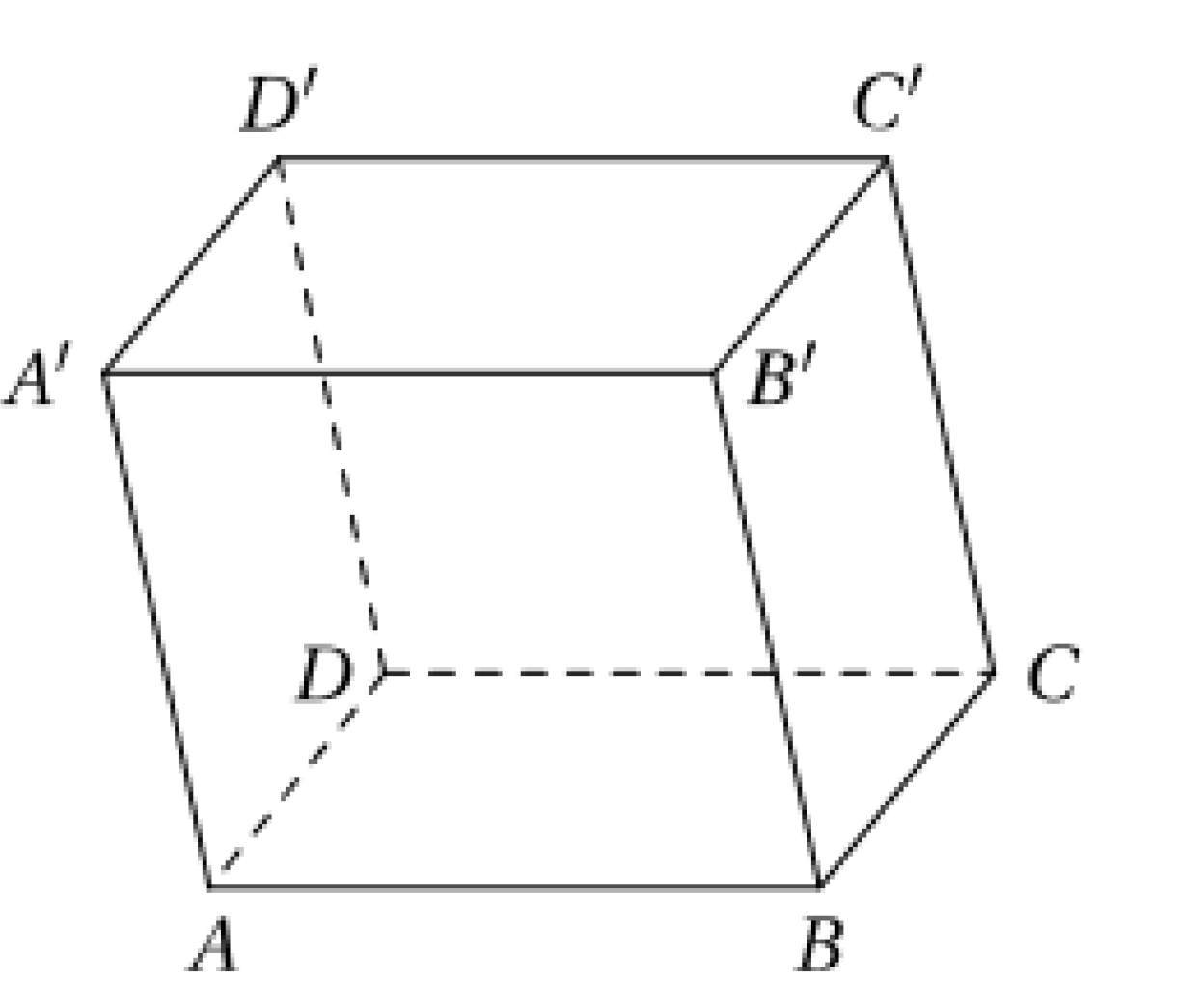
Cho lăng trụ \(ABCD.A'B'C'D'\) có hai đáy là các hình bình hành. Các điểm M, N, P lần lượt là trung điểm của cạnh AD, BC, CC' (tham khảo hình vẽ). Xét các khẳng định sau:
I) Mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(A'D'\)
II) Mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(DD'\) tại trung điểm của \(DD'\)
III) Mặt phẳng \(\left( {MNP} \right)\) song song với mặt phẳng \(\left( {ABC'D'} \right)\)
Trong các khẳng định trên, số khẳng định đúng là
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \({u_1} = 6\) và \({u_{n + 1}} = \frac{1}{9}\left( {u_n^2 - {u_n} + 25} \right)\) với mọi số tự nhiên \(n \ge 1\). Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
I) \(\left( {{u_n}} \right)\) là dãy số không tăng, không giảm.
II) \(\frac{1}{{{u_1} + 4}} = \frac{1}{{{u_1} - 5}} - \frac{1}{{{u_2} - 5}}\)
III) \(\frac{1}{{{u_1} + 4}} + \frac{1}{{{u_2} + 4}} + ... + \frac{1}{{{u_{2018}} + 4}} = 1 - \frac{1}{{{u_{2019}} - 5}}\)
Trong các mệnh đề sau, có bao nhiêu mệnh đề đúng?
I) Hàm số \(y = x + {\mathop{\rm sinx}\nolimits} \) tuần hoàn với chu kì \(T = 2\pi \)
II) Hàm số \(y = x\cos x\) là hàm số lẻ
III) Hàm số \(y = \tan x\) đồng biến trên từng khoảng xác định