 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Phương pháp:
+ Dựng mặt phẳng \(\left( \alpha \right)\) dựa vào mối quan hệ song song với \(BB',\,AC\)
+ Từ đó tính tỉ số \(\frac{{TB}}{{TC}}\)
Cách giải:
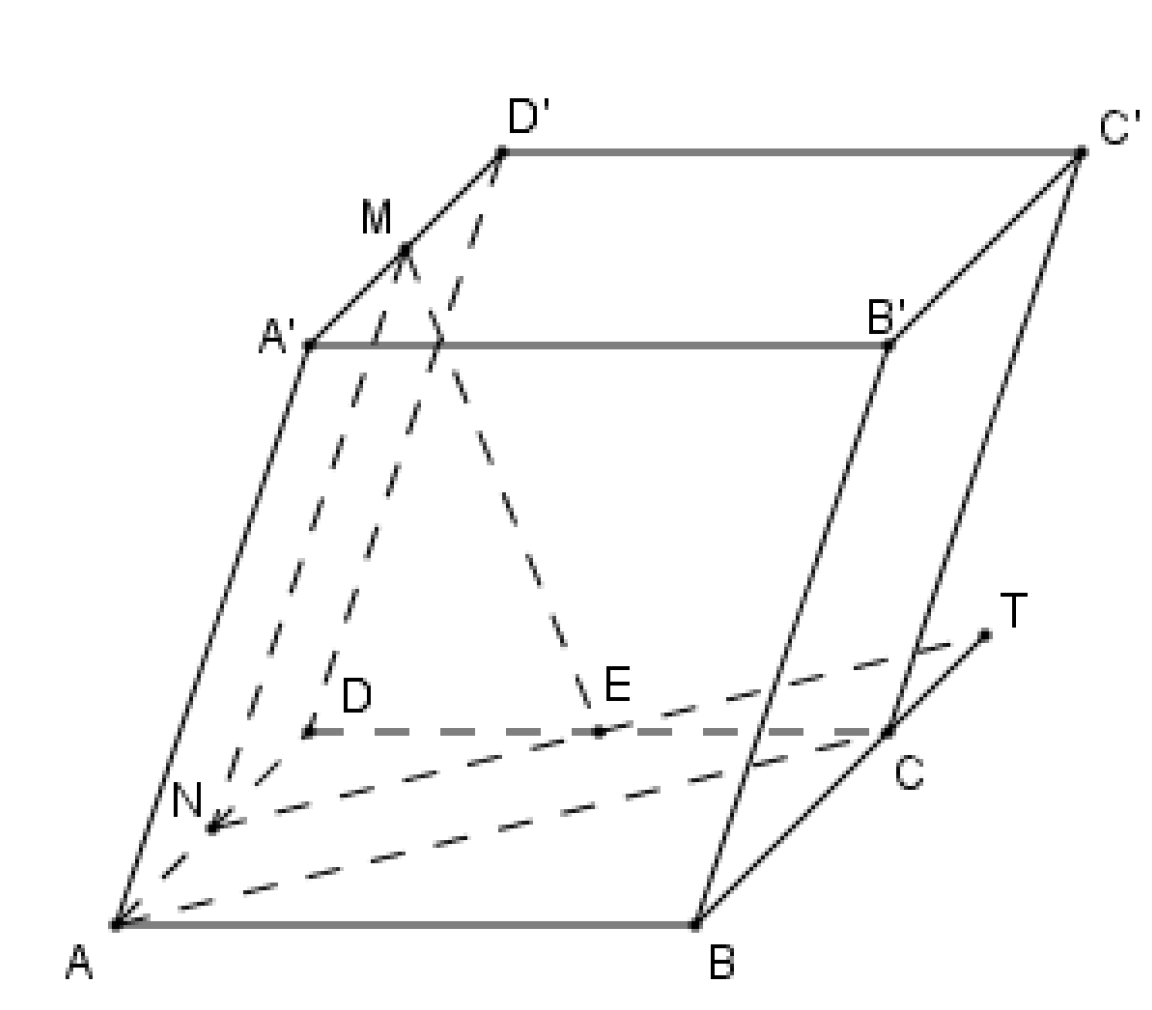
Gọi \(N,E\) lần lượt là trung điểm của \(AD,DC\)
Ta có \(MN//AA'//BB'\) và \(NE//AC\) (do \(NE\) là đường trung bình của tam giác \(DAC\))
Suy ra \(\left( \alpha \right) \equiv \left( {MNE} \right)\)
Trong \(\left( {ABCD} \right)\), kéo dài \(NE\) cắt \(BC\) tại \(T\). Suy ra \(ANTC\)là hình bình hành (do \(AN//TC;\,NT//AC\))
Do đó \(TC = AN = \frac{1}{2}AD = \frac{1}{2}BC\)
Ta có \(\left( {MNE} \right) \cap BC = \left\{ T \right\}\) nên \(\frac{{TB}}{{TC}} = \frac{{\frac{3}{2}BC}}{{\frac{1}{2}BC}} = 3\)
Cho lăng trụ \(ABCD.A'B'C'D'\) có hai đáy là các hình bình hành. Các điểm M, N, P lần lượt là trung điểm của cạnh AD, BC, CC' (tham khảo hình vẽ). Xét các khẳng định sau:
I) Mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(A'D'\)
II) Mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(DD'\) tại trung điểm của \(DD'\)
III) Mặt phẳng \(\left( {MNP} \right)\) song song với mặt phẳng \(\left( {ABC'D'} \right)\)
Trong các khẳng định trên, số khẳng định đúng là
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \({u_1} = 6\) và \({u_{n + 1}} = \frac{1}{9}\left( {u_n^2 - {u_n} + 25} \right)\) với mọi số tự nhiên \(n \ge 1\). Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
I) \(\left( {{u_n}} \right)\) là dãy số không tăng, không giảm.
II) \(\frac{1}{{{u_1} + 4}} = \frac{1}{{{u_1} - 5}} - \frac{1}{{{u_2} - 5}}\)
III) \(\frac{1}{{{u_1} + 4}} + \frac{1}{{{u_2} + 4}} + ... + \frac{1}{{{u_{2018}} + 4}} = 1 - \frac{1}{{{u_{2019}} - 5}}\)
Trong các mệnh đề sau, có bao nhiêu mệnh đề đúng?
I) Hàm số \(y = x + {\mathop{\rm sinx}\nolimits} \) tuần hoàn với chu kì \(T = 2\pi \)
II) Hàm số \(y = x\cos x\) là hàm số lẻ
III) Hàm số \(y = \tan x\) đồng biến trên từng khoảng xác định