Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Phương pháp:
Liệt kê và đếm số cách chọn 2 bạn thỏa mãn có 1 bạn nam và 1 bạn nữ tổ khác.
Các trường hợp: nam tổ I và nữ hai tổ còn lại; nam tổ II và nữ hai tổ còn lại; nam tổ III và nữ hai tổ còn lại
Cách giải:
Số cách chọn 1 bạn nam tổ I và 1 bạn nữ hai tổ còn lại là \(C_3^1.C_9^1 = 27\) cách chọn.
Số cách chọn 1 bạn nam tổ II và 1 bạn nữ hai tổ còn lại là \(C_5^1.C_{11}^1 = 55\) cách chọn.
Số cách chọn 1 bạn nam tổ III và 1 bạn nữ hai tổ còn lại là \(C_6^1.C_{12}^1 = 72\) cách chọn.
Vậy có \(27 + 55 + 72 = 154\) cách chọn.
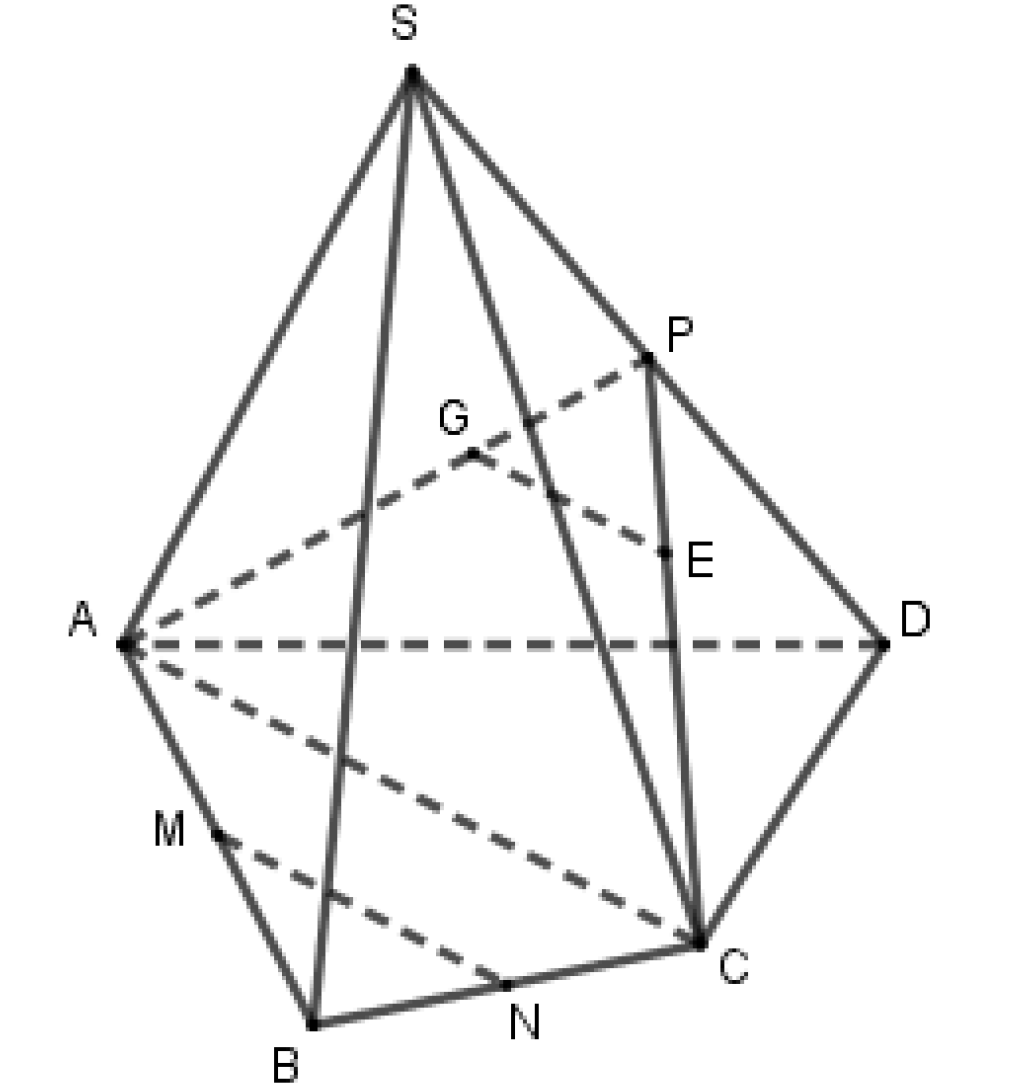
Cho lăng trụ \(ABCD.A'B'C'D'\) có hai đáy là các hình bình hành. Các điểm M, N, P lần lượt là trung điểm của cạnh AD, BC, CC' (tham khảo hình vẽ). Xét các khẳng định sau:
I) Mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(A'D'\)
II) Mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(DD'\) tại trung điểm của \(DD'\)
III) Mặt phẳng \(\left( {MNP} \right)\) song song với mặt phẳng \(\left( {ABC'D'} \right)\)
Trong các khẳng định trên, số khẳng định đúng là
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \({u_1} = 6\) và \({u_{n + 1}} = \frac{1}{9}\left( {u_n^2 - {u_n} + 25} \right)\) với mọi số tự nhiên \(n \ge 1\). Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
I) \(\left( {{u_n}} \right)\) là dãy số không tăng, không giảm.
II) \(\frac{1}{{{u_1} + 4}} = \frac{1}{{{u_1} - 5}} - \frac{1}{{{u_2} - 5}}\)
III) \(\frac{1}{{{u_1} + 4}} + \frac{1}{{{u_2} + 4}} + ... + \frac{1}{{{u_{2018}} + 4}} = 1 - \frac{1}{{{u_{2019}} - 5}}\)
Trong các mệnh đề sau, có bao nhiêu mệnh đề đúng?
I) Hàm số \(y = x + {\mathop{\rm sinx}\nolimits} \) tuần hoàn với chu kì \(T = 2\pi \)
II) Hàm số \(y = x\cos x\) là hàm số lẻ
III) Hàm số \(y = \tan x\) đồng biến trên từng khoảng xác định