Đáp án C

Phương pháp:

Nhận xét tính chất mỗi hình và tìm tâm đối xứng (nếu có)

Cách giải:

Hình chữ nhật có tâm đối xứng là giao điểm hai đường chéo.

Hình tròn có tâm đối xứng là tâm hình tròn.

Hình tam giác đều không có tâm đối xứng.

Hình bình hành có tâm đối xứng là giao điểm hai đường chéo.

Đáp án B

Phương pháp:

Giải phương trình lượng giác cơ bản: \[\cos x = \cos a \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\\x = - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\]

Sau đó dựa vào điều kiện để tìm các giá trị x phù hợp

Cách giải:

Ta có: \[\sqrt 2 \cos \left( {x + \frac{\pi }{3}} \right) = 1 \Leftrightarrow \cos \left( {x + \frac{\pi }{3}} \right) = \frac{1}{{\sqrt 2 }}\]

\[ \Leftrightarrow \cos \left( {x + \frac{\pi }{3}} \right) = \cos \frac{\pi }{4} \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{3} = \frac{\pi }{4} + k2\pi \\x + \frac{\pi }{3} = - \frac{\pi }{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \frac{\pi }{{12}} + k2\pi \\x = - \frac{{7\pi }}{{12}} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\]

Nếu \[x = - \frac{\pi }{{12}} + k2\pi \] thì \[x \in \left[ {0;\,\,2\pi } \right] \Rightarrow 0 \le - \frac{\pi }{{12}} + k2\pi \le 2\pi \Leftrightarrow \frac{1}{{24}} \le k \le \frac{{25}}{{24}} \Rightarrow k = 1 \Rightarrow x = \frac{{23\pi }}{{12}}\]

Nếu \[x = - \frac{{7\pi }}{{12}} + k2\pi \] thì \[x \in \left[ {0;\,\,2\pi } \right] \Rightarrow 0 \le - \frac{{7\pi }}{{12}} + k2\pi \le 2\pi \Leftrightarrow \frac{7}{{24}} \le k \le \frac{{31}}{{24}} \Rightarrow k = 1 \Rightarrow x = \frac{{17\pi }}{{12}}\]

Vậy có hai giá trị của x thỏa mãn đề bài.

Đáp án A

Phương pháp:

Sử dụng công thức khai triển nhị thức Newton: \[{\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n - k}}{b^k}} \]

Cách giải:

Ta có: \[{\left( {8{a^3} - \frac{b}{2}} \right)^6} = \sum\limits_{k = 0}^6 {C_6^k{{\left( {8{a^3}} \right)}^{6 - k}}.{{\left( { - \frac{b}{2}} \right)}^k}} \]

Số hạng thứ 4 ứng với \[k = 3\] nên số hạng đó là \[C_6^3{\left( {8{a^3}} \right)^{6 - 3}}.{\left( { - \frac{b}{2}} \right)^3} = - C_6^3{.8^3}.{a^9}.\frac{{{b^3}}}{8} = - 1280{a^9}{b^3}\].

Đáp án A

Phương pháp:

Sử dụng công thức khai triển nhị thức Newton: \[{\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n - k}}{b^k}} \]

Cách giải:

Ta có \[{\left( {1 + x} \right)^{2019}} = \sum\limits_{k = 0}^{2019} {C_{2019}^k{x^k}} = C_{2019}^0{x^0} + C_{2019}^1x + ... + C_{2019}^{2019}{x^{2019}}\]

Với \[x = 1\] ta có \[{\left( {1 + 1} \right)^{2019}} = C_{2019}^0 + C_{2019}^1 + C_{2019}^2 + ... + C_{2019}^{2019}\]

Hay \[C_{2019}^0 + C_{2019}^1 + C_{2019}^2 + ... + C_{2019}^{2019} = {2^{2019}}\]

Đáp án D

Phương pháp:

Biến đổi phương trình về dạng \[\cos x = \cos \alpha \Leftrightarrow x = \pm \alpha + k2\pi \]

Cách giải:

Ta có: \[2\cos x + 1 = 0 \Leftrightarrow \cos x = - \frac{1}{2} \Leftrightarrow \cos x = \cos \frac{{2\pi }}{3} \Leftrightarrow x = \pm \frac{{2\pi }}{3} + k2\pi \].

Đáp án B

Phương pháp:

Sử dụng công thức tọa độ của phép vị tự \[{V_{\left( {O;k} \right)}}\left( A \right) = A' \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = k{x_A}\\{x_{B'}} = k{x_B}\end{array} \right.\]

Đường tròn tâm \[I\left( {a;\,\,b} \right)\] bán kính R có phương trình \[{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\]

Cách giải:

Đường tròn (C) có tâm \[I\left( {8;\,\,4} \right)\]và bán kính \[R = 2\]

Gọi \[I'\left( {x;\,\,y} \right)\] là ảnh của \[I\left( {8;\,\,4} \right)\] qua \[{V_{\left( {O;3} \right)}}\]

Ta có \[\left\{ \begin{array}{l}x = 3.8 = 24\\y = 3.4 = 12\end{array} \right. \Rightarrow I'\left( {24;\,\,12} \right)\].

Ảnh của đường tròn (C) qua phép vị tự tâm O tỉ số \[k = 3\]là đường tròn \[\left( {C'} \right)\] có tâm \[I'\left( {24;\,\,12} \right)\] và bán kính \[R' = k.R = 3.2 = 6\].

Phương trình đường tròn \[\left( {C'} \right):{\left( {x - 24} \right)^2} + {\left( {y - 12} \right)^2} = 36\]

Đáp án D

Phương pháp:

Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

- Viết dạng phương trình của đường thẳng \[\Delta '\]

- Lấy một điểm \[A \in \Delta \], tìm ảnh \[A'\] của A qua phép tịnh tiến

- Cho \[A' \in \Delta '\] suy ra phương trình \[\Delta '\]

Cách giải:

Gọi phương trình \[\Delta '||\Delta \] có dạng \[\Delta ':x + 2y + c = 0\]

Lấy \[A\left( {1;\,\,0} \right) \in \Delta \], khi đó \[{T_{\overrightarrow v }}\left( A \right) = A' \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = 1 + 1 = 2\\{y_{A'}} = 0 - 1 = - 1\end{array} \right. \Rightarrow A'\left( {2;\,\, - 1} \right)\]

\[A' \in \Delta ' \Leftrightarrow 2 + 2.\left( { - 1} \right) + c = 0 \Leftrightarrow c = 0\]

Vậy phương trình \[\Delta ':x + 2y = 0\]

Đáp án B

Phương pháp:

Sử dụng công thức tọa độ của phép đối xứng tâm

Cách giải:

Ảnh của A qua phép đối xứng tâm \[O\left( {0;\,\,0} \right)\] là A'.

Ta có \[\left\{ \begin{array}{l}{x_{A'}} = 2.0 - 1 = - 1\\{y_{A'}} = 2.0 - \left( { - 3} \right) = 3\end{array} \right. \Rightarrow A'\left( { - 1;\,\,3} \right)\]

Đáp án A

Phương pháp:

- Biến đổi phương trình về dạng phương trình đối xứng đối với sin và cos.

- Sử dụng phương pháp đặt ẩn phụ \[t = \sin x + \cos x\] để giải phương trình này.

Cách giải:

Ta có: \[\sin x + \cos x = 1 - \frac{1}{2}\sin 2x \Leftrightarrow \sin x + \cos x = 1 - \sin x\cos x\]

Đặt \[\sin x + \cos x = t\,\,\left( { - \sqrt 2 \le t \le \sqrt 2 } \right)\]\[ \Rightarrow \sin x\cos x = \frac{{{t^2} - 1}}{2}\].

Khi đó phương trình trở thành:

\[t = 1 - \frac{{{t^2} - 1}}{2} = 0 \Leftrightarrow 2t + {t^2} - 1 - 2 = 0 \Leftrightarrow {t^2} + 2t - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1 & \left( {tm} \right)\\t = - 3 & \left( {ktm} \right)\end{array} \right.\]

Suy ra \[\sin x + \cos x = 1 \Leftrightarrow \sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right) = 1 \Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = \frac{1}{{\sqrt 2 }}\]

\[ \Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = \sin \frac{\pi }{4} \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{4} = \frac{\pi }{4} + k2\pi \\x + \frac{\pi }{4} = \frac{{3\pi }}{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k2\pi \\x = \frac{\pi }{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\]

Do x là nghiệm âm lớn nhất nên:

+ TH1: \[k2\pi < 0 \Leftrightarrow k < 0\mathop \Rightarrow \limits^{k \in \mathbb{Z}} k = - 1 \Rightarrow x = - 2\pi \]

+ TH2: \[\frac{\pi }{2} + k2\pi < 0 \Leftrightarrow k < - \frac{1}{4}\mathop \Rightarrow \limits^{k \in \mathbb{Z}} k = - 1 \Rightarrow x = - \frac{{3\pi }}{2}\]

Trong hai nghiệm \[ - 2\pi \] và \[ - \frac{{3\pi }}{2}\] thì nghiệm âm lớn nhất là \[ - \frac{{3\pi }}{2}\].

Đáp án C

Phương pháp:

Hàm số \[y = \cos ax\] tuần hoàn với chu kì \[T = \frac{{2\pi }}{{\left| a \right|}}\]

Cách giải:

Hàm số \[y = \cos \frac{x}{2}\] tuần hoàn với chu kì \[T = \frac{{2\pi }}{{\frac{1}{2}}} = 4\pi \]

Đáp án D

Phương pháp:

Sử dụng tính chất phép quay có góc quay \[k2\pi \]

Cách giải:

Phép quay tâm O góc quay \[\alpha = k2\pi \] biến một điểm bất kì thành chính nó.

Vậy có vô số điểm thỏa mãn bài toán.

Đáp án C

Phương pháp:

Phép vị tự tâm I tỉ số k biến M thành M' thì \[\overrightarrow {IM'} = k\overrightarrow {IM} \]

Cách giải:

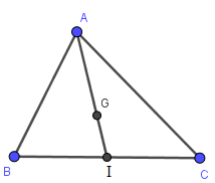
Gọi I là trung điểm của BC.

Vì G là trọng tâm tam giác ABC, ta có \[IG = \frac{1}{3}IA\] suy ra \[\overrightarrow {IG} = \frac{1}{3}\overrightarrow {IA} \] nên phép vị tự tâm I tỉ số \[\frac{1}{3}\] biến A thành G.

Mà điểm A chạy trên đường tròn \[\left( {O;\,\,R} \right)\] cố định nên quỹ tích điểm G là ảnh của đường tròn \[\left( {O;\,\,R} \right)\] qua phép vị tự tâm I tỉ số \[\frac{1}{3}\].

Đáp án B

Phương pháp:

Sử dụng công thức biến đổi tọa độ của phép đối xứng qua trục Ox là \[\left\{ \begin{array}{l}x' = x\\y' = - y\end{array} \right.\]

Có thể nhớ mẹo như sau : Đối xứng qua đâu thì giữ nguyên cái đó, còn lại lấy đối. Cụ thể: đối xứng qua trục Ox thì giữ nguyên giá trị x và lấy đối giá trị y.

Cách giải:

Qua phép đối xứng trục Ox thì điểm \[M\left( { - 2;\,\,3} \right)\] biến thành điểm \[M'\left( { - 2;\,\, - 3} \right)\].

Đáp án B

Phương pháp:

Nhận xét tính đúng sai của từng đáp án, sử dụng tính chất phép vị tự, đồng dạng.

Cách giải:

Đáp án A: Phép vị tự tỉ số k là phép đồng dạng tỉ số \[\left| k \right|\]: Đúng.

Đáp án B: Phép đồng dạng là phép biến hình: Sai vì nêu tỉ số đồng dạng khác 1 thì nó làm thay đổi khoảng cách giữa các điểm.

Đáp án D

Phương pháp:

Sử dụng công thức khai triển nhị thức Newton: \[{\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n - k}}{b^k}} \]

Cách giải:

Ta có \[{\left( {{x^2} - 3x} \right)^{10}} = \sum\limits_{k = 0}^{10} {C_{10}^k{{\left( {{x^2}} \right)}^{10 - k}}.{{\left( { - 3x} \right)}^k}} = \sum\limits_{k = 0}^{10} {C_{10}^k.{{\left( { - 3} \right)}^k}.{x^{20 - k}}} \]

Hệ số của \[{x^{16}}\] trong khai triển ứng với \[20 - k = 16 \Leftrightarrow k = 4\]

Hệ số cần tìm là \[C_{10}^4.{\left( { - 3} \right)^4} = 17010\].

Đáp án C

Phương pháp:

- Tính số phần tử của không gian mẫu \[n\left( \Omega \right)\]

- Tính số khả năng có lợi cho biến cố.

- Tính xác suất theo công thức \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\]

Cách giải:

Số cách chọn 2 quả cầu trong hộp là: \[C_7^2\]

Số cách chọn được 2 quả cầu vàng là \[C_4^2\]

Xác suất cần tính: \[P\left( A \right) = \frac{{C_4^2}}{{C_7^2}} = \frac{2}{7}\].

Đáp án D

Phương pháp:

Sử dụng phép quay tâm I góc quay \[\alpha \] biến M thành M’ thì \[OM = OM'\] và \[\angle \left( {OM;\,\,OM'} \right) = \alpha \]

Cách giải:

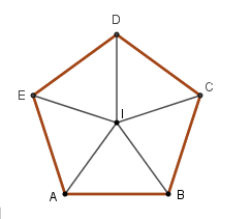
Vì ABCDE là ngũ giác đều tâm I nên \[IA = IB = IC = ID = IE\] và \[\widehat {CID} = \widehat {DIE} = \widehat {EIA} = \widehat {AIB} = \widehat {BIC} = \frac{{360^\circ }}{5} = 72^\circ \]

Từ đó ta có

\[{Q_{\left( {I;144^\circ } \right)}}\left( C \right) = E;\,\,{Q_{\left( {I;\,\,144^\circ } \right)}}\left( D \right) = A \Rightarrow {Q_{\left( {I;\,\,144^\circ } \right)}}\left( {CD} \right) = EA\] nên A đúng

\[{Q_{\left( {I;\,\,72^\circ } \right)}}\left( A \right) = B;\,\,{Q_{\left( {I;\,\,72^\circ } \right)}}\left( B \right) = C \Rightarrow {Q_{\left( {I;\,\,72^\circ } \right)}}\left( {AB} \right) = BC\] nên B đúng

\[{Q_{\left( {I;\,\,72^\circ } \right)}}\left( A \right) = B;\,\,{Q_{\left( {I;\,\,72^\circ } \right)}}\left( E \right) = A \Rightarrow {Q_{\left( {I;\,\,72^\circ } \right)}}\left( {AE} \right) = BA\] nên C đúng

\[{Q_{\left( {I;\,\,144^\circ } \right)}}\left( B \right) = D;\,\,{Q_{\left( {I;\,\,144^\circ } \right)}}\left( C \right) = E \Rightarrow {Q_{\left( {I;\,\,144^\circ } \right)}}\left( {BC} \right) = DE\] nên D sai.

Đáp án B

Phương pháp:

Sử dụng công thức tính xác suất của biến cố đối: \[P\left( {\overline A } \right) = 1 - P\left( A \right)\]

Cách giải:

Nếu A và \[\overline A \] là hai biến cố đối nhau thì \[P\left( {\overline A } \right) = 1 - P\left( A \right) \Leftrightarrow P\left( A \right) = 1 - P\left( {\overline A } \right)\]

Đáp án B

Phương pháp:

Sử dụng kiến thức về tổ hợp

Cách giải:

Cả lớp có \[15 + 17 = 32\] bạn

Như vậy có \[C_{32}^1 = 32\] cách chọn 1 bạn làm lớp trưởng

Đáp án C

Phương pháp:

Tính tổng 2019S bằng cách nhận xét số hạng tổng quát của tổng này

Cách giải:

Ta có: \[S = C_{2018}^0 + \frac{1}{2}C_{2018}^1 + \frac{1}{3}C_{2018}^2 + ... + \frac{1}{{2018}}C_{2018}^{2017} + \frac{1}{{2019}}C_{2018}^{2018} = \sum\limits_{K = 0}^{2018} {\frac{1}{{k + 1}}C_{2018}^k} \]

\[ \Rightarrow 2019S = \sum\limits_{k = 0}^{2018} {\frac{{2019}}{{k + 1}}} C_{2018}^k = \sum\limits_{k = 0}^{2018} {\frac{{2019}}{{k + 1}}} .\frac{{2018!}}{{k!\left( {2018 - k} \right)!}} = \sum\limits_{k = 0}^{2018} {\frac{{2019!}}{{\left( {k + 1} \right)!\left( {2019 - \left( {k + 1} \right)} \right)!}}} = \sum\limits_{k = 0}^{2018} {C_{2019}^{k + 1}} \]

\[ = C_{2019}^1 + C_{2019}^2 + ... + C_{2019}^{2019} \Rightarrow 2019S + C_{2019}^0 + C_{2019}^1 + C_{2019}^2 + ... + C_{2019}^{2019} = {2^{2019}}\]

\[ \Rightarrow 2019 = {2^{2019}} - C_{2019}^0 = {2^{2019}} - 1 \Rightarrow S = \frac{{{2^{2019}} - 1}}{{2019}}\]

Đáp án B

Phương pháp:

Sử dụng công thức \[{\cos ^2}x = \frac{{1 + \cos 2x}}{2}\] và \[\cos \left( {a + b} \right) = \cos a.\cos b - \sin a\sin b\]

Sử dụng \[ - 1 \le \cos \le 1\]

Cách giải:

Ta có \[y = 2{\cos ^2}x + \sin 2x = 2.\frac{{1 + \cos 2x}}{2} + \sin 2x = 1 + \cos 2x + \sin 2x\]

\[ \Rightarrow \frac{y}{{\sqrt 2 }} = \frac{1}{{\sqrt 2 }} + \frac{1}{{\sqrt 2 }}\cos 2x + \frac{1}{{\sqrt 2 }}\sin 2x = \frac{1}{{\sqrt 2 }} + \cos 2x\cos \frac{\pi }{4} + \sin 2x.\sin \frac{\pi }{4} = \frac{1}{{\sqrt 2 }} + \cos \left( {2x - \frac{\pi }{4}} \right)\]

Ta có \[\cos \left( {2x - \frac{\pi }{4}} \right) \ge - 1 \Leftrightarrow \frac{1}{{\sqrt 2 }} + \cos \left( {2x - \frac{\pi }{4}} \right) \ge - 1 + \frac{1}{{\sqrt 2 }}\]

Hay \[\frac{y}{{\sqrt 2 }} \ge - 1 + \frac{1}{{\sqrt 2 }} \Leftrightarrow y \ge 1 - \sqrt 2 \]

Dấu “=” xảy ra khi \[\cos \left( {2x - \frac{\pi }{4}} \right) = - 1 \Leftrightarrow 2x - \frac{\pi }{4} = - \pi + k2\pi \Leftrightarrow x = \frac{{ - 3\pi }}{8} + k\pi \left( {k \in \mathbb{Z}} \right)\]

Vậy giá trị nhỏ nhất của y là \[1 - \sqrt 2 \].

Đáp án B

Phương pháp:

- Tìm ĐKXĐ

- Biến đổi phương trình về dạng \[\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\]

Cách giải:

Điều kiện: \[\sin x \ne 0 \Leftrightarrow x \ne k\pi \]

Khi đó, phương trình \[ \Leftrightarrow \sin 5x = 2\sin x\cos x \Leftrightarrow \sin 5x = \sin 2x\]

\[ \Leftrightarrow \left[ \begin{array}{l}5x = 2x + k2\pi \\5x = \pi - 2x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}3x = k2\pi \\7x = \pi + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{k2\pi }}{3}\\x = \frac{\pi }{7} + \frac{{k2\pi }}{7}\end{array} \right.\]

Nếu \[x = \frac{{k2\pi }}{3}\] thì \[x \in \left( {0;\,\,\pi } \right) \Rightarrow 0 < \frac{{k2\pi }}{3} < \pi \Leftrightarrow 0 < k < \frac{3}{2} \Rightarrow k = 1 \Rightarrow x = \frac{{2\pi }}{3}\,\,(TM)\]

Nếu \[x = \frac{\pi }{7} + \frac{{k2\pi }}{7}\] thì \[x \in \left( {0;\,\,\pi } \right) \Rightarrow 0 < \frac{\pi }{7} + \frac{{k2\pi }}{7} < \pi \Leftrightarrow 0 < \pi + k2\pi < 7\pi \Leftrightarrow - \frac{1}{2} < k < 3\]

\[ \Rightarrow k \in \left\{ {0;\,\,1;\,\,2} \right\} \Rightarrow x \in \left\{ {\frac{\pi }{7};\,\,\frac{{3\pi }}{7};\,\,\frac{{5\pi }}{7}} \right\}\]

Vậy phương trình đã cho có 4 nghiệm trong khoảng \[\left( {0;\,\,\pi } \right)\].

Đáp án C

Phương pháp:

- Tìm số phần tử của không gian mẫu \[n\left( \Omega \right)\]

- Tính số khả năng có lợi cho biến cố.

- Tính xác suất theo công thức \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\]

Cách giải:

Gọi số có số tự nhiên có bốn chữ số phân biệt là \[\overline {abcd} ,\,\,\left( {a,b,c,d \in \left\{ {0;1;2;3;4;5;6;7;8;9} \right\}} \right)\]

+ a có 9 cách chọn, b có 9 cách chọn, c có 8 cách chọn, d có 7 cách chọn

Nên có \[9.9.8.7 = 4536\] số. Hay số phần tử của không gian mẫu là \[n\left( \Omega \right) = 4536\]

Gọi A là biến cố \[\overline {abcd} > 2500\]

+ Nếu \[a \in \left\{ {3;4;5;6;7;8;9} \right\}\] thì số cách chọn 3 chữ số b, c, d là \[A_9^3\] nên có \[7.A_9^3\] số

+ Nếu \[a = 2\] và \[b = 5\] thì \[c,d \in \left\{ {0;1;2;3;4;5;6;7;8;9} \right\}\] nên có \[A_8^2\] số

+ Nếu \[a = 2;\,\,b \in \left\{ {6;7;8;9} \right\}\] thì có \[A_8^2\] cách chọn c, d nên có \[4.A_8^2\] số

Số phần tử của biến cố A là \[n\left( A \right) = 7.A_9^3 + A_8^2 + 4.A_8^2 = 3808\]

Xác suất cần tìm là \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{3808}}{{4536}} = \frac{{68}}{{81}}\]

Đáp án B

Phương pháp:

- Biểu thức \[\tan x\] xác định nếu \[\cos x \ne 0\]

- Biểu thức \[\frac{1}{{\sqrt {f\left( x \right)} }}\] xác định nếu \[f\left( x \right) > 0\]

Cách giải:

ĐKXĐ: \[\left\{ \begin{array}{l}\cos x \ne 0\\2 - \cos x > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\cos x \ne 0\\\cos x < 2\,\,\left( {\forall x} \right)\end{array} \right. \Leftrightarrow \cos x \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi \]

Vậy TXĐ: \[D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\].

Đáp án C

Phương pháp:

- Tính số phần tử của không gian mẫu \[n\left( \Omega \right)\]

- Tính số khả năng có lợi cho biến cố.

- Tính xác suất theo công thức \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\]

Cách giải:

Số phần tử của không gian mẫu \[n\left( \Omega \right) = A_9^6\]

Gọi A là biến cố: “số có 6 chữ số chỉ chứa ba chữ số chẵn”

Như vậy số đó có 3 chữ số chẵn và 3 chữ số lẻ.

Số cách chọn 3 chữ số chẵn từ 4 chữ số chẵn là \[C_4^3\]

Số cách chọn 3 chữ số lẻ từ 5 chữ số lẻ là \[C_5^3\]

Số cách lập ra số có 6 chữ số mà chỉ có 3 chữ số chẵn từ 9 số đã cho là \[n\left( A \right) = 6!.C_4^3.C_5^3\]

Xác suất cần tìm là \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{6!.C_4^3.C_5^3}}{{A_9^6}} = \frac{{10}}{{21}}\]

Đáp án E

Phương pháp:

Hàm số \[y = f\left( x \right)\] được gọi là chẵn trên D nếu với \[x \in D\] thì \[ - x \in D\] và \[f\left( { - x} \right) = f\left( x \right)\]

Cách giải:

Đáp án A: TXĐ: \[D = \mathbb{R}\]

Có \[f\left( { - x} \right) = \sin \left( { - 2x} \right) + 1 = - \sin 2x + 1 \ne f\left( x \right)\] nên hàm số này không chẵn không lẻ

Đáp án B: TXĐ: \[D = \mathbb{R}\]

Có \[f\left( { - x} \right) = \sin \left( { - x} \right).\cos \left( { - 2x} \right) = - \sin x.\cos 2x = - f\left( x \right)\] nên hàm số này lẻ

Đáp án C: TXĐ: \[D = \mathbb{R}\]

Có \[f\left( { - x} \right) = \sin \left( { - x} \right).\sin \left( { - 3x} \right) = \left( { - \sin x} \right).\left( { - \sin 3x} \right) = \sin x.\sin 3x = f\left( x \right)\] nên hàm số này chẵn

Đáp án D: TXĐ: \[D = \mathbb{R}\]

Có \[f\left( { - x} \right) = \sin \left( { - 2x} \right) + \sin \left( { - x} \right) = - \sin 2x - \sin x = - \left( {\sin 2x + \sin x} \right) = - f\left( x \right)\] nên hàm số này lẻ

Vậy có hai đáp án đúng là A và C

Đáp án C

Phương pháp:

- Tính số phần tử của không gian mẫu \[n\left( \Omega \right)\]

- Tính số khả năng có lợi cho biến cố.

- Tính xác suất theo công thức \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\]

Cách giải:

Số phần tử của không gian mẫu: \[n\left( \Omega \right) = C_{100}^3\]

Gọi A là biến cố “chọn được 3 tấm thẻ có tổng các số ghi trên thẻ là số chia hết cho 2”

TH1: Chọn được cả 3 tấm thẻ mang số chẵn. Khi đó có \[C_{50}^3\] cách chọn

TH2: Chọn được hai tấm thẻ mang số lẻ và một tấm thẻ mang số chẵn. Khi đó có \[C_{50}^2C_{50}^1\] cách chọn

Số phần tử của biến cố A là \[n\left( A \right) = C_{50}^3 + C_{50}^2C_{50}^1\]

Xác suất cần tìm là \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{50}^3 + C_{50}^2C_{50}^1}}{{C_{100}^3}} = \frac{1}{2}\]

Đáp án A

Phương pháp:

Sử dụng công thức \[A_k^n = \frac{{n!}}{{\left( {n - k} \right)!}}\] biến đổi và giải phương trình

Cách giải:

Ta có:

\[2A_n^4 = 3A_{n - 1}^4 \Leftrightarrow 2.\frac{{n!}}{{\left( {n - 4} \right)!}} = 3.\frac{{\left( {n - 1} \right)!}}{{\left( {n - 5} \right)!}} \Leftrightarrow 2n\left( {n - 1} \right)\left( {n - 2} \right)\left( {n - 3} \right) = 3.\left( {n - 1} \right)\left( {n - 2} \right)\left( {n - 3} \right)\left( {n - 4} \right)\]

\[ \Leftrightarrow 2n = 3\left( {n - 4} \right) \Leftrightarrow 2n = 3n - 12 \Leftrightarrow n = 12\].

Chú ý:

Có thể sử dụng cách thử đáp án bằng MTCT, chức năng CALC

Nhập vào màn hình \[2XP4 - 3\left( {X - 1} \right)P4\] rồi bấm CALC, nhập các giá trị ở mỗi đáp án rồi ấn “=”, nếu được kết quả bằng 0 thì chọn.

Đáp án C

Phương pháp:

Sử dụng kiến thức về hoán vị để làm bài

Cách giải:

Coi 5 quyển sách Văn chỉ xếp vào 1 chỗ. Như vậy ta sẽ xếp 5 quyển sách Văn và 7 quyển sách Toán vào 8 vị trí trên kệ sách.

Số cách xếp 5 quyển sách Văn là 5!.

Số cách xếp xếp 5 quyển sách Văn và 7 quyển sách Toán trên kệ sách dài sao cho 5 quyển sách Văn xếp kề nhau là 5!.8! cách.

Phương pháp:

a) Sử dụng công thức khai triển nhị thức Newton: \[{\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n - k}}{b^k}} \]

b) Đếm số phần tử của không gian mẫu: Số các số có 4 chữ số lập được từ các chữ số đã cho.

Đếm số các số chia hết cho 5 trong tập hợp trên và suy ra xác suất.

Cách giải:

a) Ta có: \[{\left( {2{x^2} + \frac{1}{{{x^3}}}} \right)^5} = \sum\limits_{k = 0}^5 {C_5^k{{\left( {2{x^2}} \right)}^{5 - k}}.{{\left( {\frac{1}{{{x^3}}}} \right)}^k}} \]

\[ = \sum\limits_{k = 0}^5 {C_5^k{{.2}^{5 - k}}.{{\left( {\frac{1}{{{x^3}}}} \right)}^k}} = \sum\limits_{k = 0}^5 {C_5^k{{.2}^{5 - k}}.{x^{10 - 2k - 3k}}} = \sum\limits_{k = 0}^5 {C_5^k{{.2}^{5 - k}}.{x^{10 - 5k}}} \]

Số hạng không chứa x ứng với \[10 - 5k = 0 \Leftrightarrow k = 2\] nên hệ số \[C_5^2{.2^{5 - 2}} = 80\]

Vậy số hạng không chứa x trong khai triển là 80.

b) Số cách chọn 4 trong 8 chữ số 0; 1; 2; 3; 4; 5; 6; 7 có phân biệt thứ tự là \[A_8^4\]

Nếu chữ số 0 ở đầu thì có \[A_7^3\] số thỏa mãn.

Do đó số các số có 4 chữ số phân biệt lập được là \[A_8^4 - A_7^3\].

Gọi số có 4 chữ số chia hết cho 5 là \[\overline {abcd} \], với \[a,b,c,d \in \left\{ {0;1;2;3;4;5;6;7} \right\}\]

Vì \[\overline {abcd} \vdots 5\] nên \[d = 0\] hoặc \[d = 5\]

+) Nếu \[d = 0\] thì \[a \in \left\{ {1;2;3;4;5;6;7} \right\}\] có 7 cách chọn.

\[b \ne a,d \Rightarrow \] b có 6 cách chọn.

\[c \ne a,b,d\] nên có 5 cách chọn.

Có \[7.6.5 = 210\] số tự nhiên có bốn chữ số, tận cùng bằng 0 được lập từ các chữ số \[0;1;2;3;4;5;6;7\]

+) Nếu \[d = 5\] thì \[a \in \left\{ {1;2;3;4;5;6;7} \right\}\] có 6 cách chọn.

\[b \ne a,d \Rightarrow \] b có 6 cách chọn.

\[c \ne a,b,d\] nên có 5 cách chọn.

Có \[6.6.5 = 180\] số tự nhiên có bốn chữ số, tận cùng bằng 5 được lập từ các chữ số \[0;1;2;3;4;5;6;7\].

Do đó có \[210 + 180 = 390\] số có bốn chữ số chia hết cho 5 được lập từ các chữ số \[0;1;2;3;4;5;6;7\].

Vậy xác suất là \[P = \frac{{390}}{{A_8^4 - A_7^3}} = \frac{{390}}{{1470}} = \frac{{13}}{{49}}\].

Phương pháp:

+ Sử dụng cách tìm giao tuyến hai mặt phẳng, tìm giao điểm của đường thẳng và mặt phẳng

+ Sử dụng định lý Ta-lét để tìm tỉ số

Cách giải:

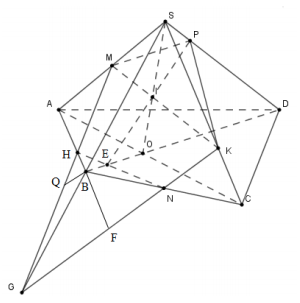
a)

* Trong \[\left( {SBC} \right)\], kéo dài NK cắt SB tại G

Khi đó \[\left\{ \begin{array}{l}MG \subset \left( {MNK} \right)\\MG \subset \left( {SBC} \right)\end{array} \right.\] nên \[\left( {MNK} \right) \cap \left( {SAB} \right) = MG\]

* Trong (SAB), gọi MG cắt AB tại H

Khi đó \[\left\{ \begin{array}{l}H \in MG \subset \left( {MNK} \right)\\H \in AB\end{array} \right.\] nên H là giao điểm của AB với (MNK)

b)

* Xác định thiết diện

Gọi \[AC \cap BD = \left\{ O \right\}\], trong (SAC) có \[SO \cap MK = \left\{ I \right\}\]

Trong (ABCD) có \[BD \cap HN = \left\{ E \right\}\]

Trong (SBD) có \[EI \cap SD = \left\{ P \right\}\]

Khi đó ta có \[\left( {MNK} \right) \equiv \left( {MPKNH} \right)\]

Hay \[\left\{ \begin{array}{l}\left( {MNK} \right) \cap \left( {SBC} \right) = NK\\\left( {MNK} \right) \cap \left( {SAB} \right) = MH\\\left( {MNK} \right) \cap \left( {SAD} \right) = MP\\\left( {MNK} \right) \cap \left( {SDC} \right) = PK\\\left( {MNK} \right) \cap \left( {ABCD} \right) = NH\end{array} \right.\]

Nên thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (MNK) là ngũ giác PMHNK.

* Tính tỉ số \[\frac{{HA}}{{HB}}\]

Trong ∆SQK kẻ \[BF//SK\left( {F \in QK} \right)\]

Khi đó \[\frac{{NB}}{{NC}} = \frac{{KC}}{{BF}}\] (theo Ta-let) mà \[NB = NC \Rightarrow KC = BF\]

Mà \[\frac{{KC}}{{SK}} = \frac{1}{2}\] suy ra \[\frac{{BF}}{{SK}} = \frac{1}{2}\] mà \[BF//SK \Rightarrow \] BF là đường trung bình của ∆GQK.

Do đó B là trung điểm của SG

Trong ∆GMS kẻ \[BQ//SA\left( {Q \in GM} \right)\] mà B là trung điểm của SG nên QB là đường trung bình của ∆GSM

Suy ra \[\frac{{QB}}{{SM}} = \frac{1}{2} \Rightarrow \frac{{QB}}{{MA}} = \frac{1}{2}\] (do \[SM = MA\])

Vì \[QB//AM\], theo định lét Ta-let ta có \[\frac{{QB}}{{MA}} = \frac{{HB}}{{HA}} = \frac{1}{2} \Rightarrow \frac{{HA}}{{HB}} = 2\].