Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 1)
-
3813 lượt thi
-
29 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Trong các phương trình sau, phương trình nào có nghiệm?
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Đưa các phương trình về dạng phương trình tích.
Sử dụng các phương trình lượng giác cơ bản \[\sin x = a;\cos x = a,\tan x = b,\cot x = b\] với \[ - 1 \le a \le 1\].
Cách giải:
Đáp án A: \[{\sin ^2}x + \sin x - 6 = 0 \Leftrightarrow \left( {\sin x + 3} \right)\left( {\sin x - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}\sin x = - 3\left( {VN} \right)\\\sin x = 2\;\left( {VN} \right)\end{array} \right.\].
Nên loại A.
Đáp án B: \[\cos x = \frac{\pi }{2}\] vô nghiệm vì \[\frac{\pi }{2} > 1\], do đó loại B.
Đáp án C: \[{\cot ^2}x - \cot x + 5 = 0 \Leftrightarrow {\left( {\cot x - \frac{1}{2}} \right)^2} + \frac{{19}}{4} = 0\] (vô nghiệm) nên loại C.
Đáp án D: \[\begin{array}{l}2\cos 2x - \cos x - 3 = 0 \Leftrightarrow 2\left( {2{{\cos }^2}x - 1} \right) - \cos x - 3 = 0\\ \Leftrightarrow 4{\cos ^2}x - \cos x - 5 = 0 \Leftrightarrow \left[ \begin{array}{l}\cos x = - 1\\\cos x = \frac{5}{4}\left( {VN} \right)\end{array} \right. \Rightarrow x = \pi + k2\pi \left( {k \in \mathbb{Z}} \right)\end{array}\]
Câu 2:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp
Sử dụng kiến thức về chu kì tuần hoàn của hàm số \[y = \sin x\].
Cách giải
Hàm số \[y = \sin x\] tuần hoàn với chu kì \[T = 2\pi \].
Câu 3:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp
Sử dụng khai triển nhị thức Niu-ton: \[{\left( {a - b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n - k}}{b^k}} \]
Từ đó tìm hệ số của \[{x^3}\] trong khai triển.
Cách giải:
Ta có: \[{\left( {1 - 2x} \right)^8} = \sum\limits_{k = 0}^8 {C_8^k{{\left( { - 2x} \right)}^k}} = \sum\limits_{k = 0}^8 {C_8^k{{\left( { - 2} \right)}^k}} {x^k}\].
Số hạng chứa \[{x^3}\] ứng với \[k = 3\].
Suy ra hệ số cần tìm là: \[C_8^3.{\left( { - 2} \right)^3} = - 448\].
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp
Sử dụng biểu thức tọa độ của phép vị tự tâm \[I\left( {a;b} \right)\] biến \[M\left( {x;y} \right)\] thành \[M'\left( {x';y'} \right)\] thì \[\left\{ \begin{array}{l}x' = kx + \left( {1 - k} \right)a\\y' = ky + \left( {1 - k} \right)b\end{array} \right.\]
Sử dụng biểu thức tọa độ của phép tịnh tiến theo véctơ \[\overrightarrow v = \left( {a;b} \right)\] biến \[M\left( {x;y} \right)\] thành \[M'\left( {x';y'} \right)\] thì \[\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\].
Cách giải
Gọi \[M\left( {x;y} \right) \in d:3x - y - 3 = 0\]
Gọi \[M'\left( {x';y'} \right)\] là ảnh của \[M\left( {x;y} \right)\] qua phép vị tự tâm \[I\left( {2;3} \right)\] tỉ số \[k = - 1\].
Khi đó ta có \[\left\{ \begin{array}{l}x' = - x + \left( {1 - \left( { - 1} \right)} \right).2\\y' = - y + \left( {1 - \left( { - 1} \right)} \right).3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - x' + 4\\y = - y' + 6\end{array} \right.\] nên \[M\left( { - x' + 4; - y' + 6} \right)\]
Mà \[M\left( { - x' + 4; - y' + 6} \right) \in d:3x - y - 3 = 0\] nên ta có \[\begin{array}{l}3\left( { - x' + 4} \right) - \left( { - y' + 6} \right) = 0 \Leftrightarrow - 3x' + 12 + y' - 6 - 3 = 0\\ \Leftrightarrow - 3x' + y' + 3 = 0 \Leftrightarrow 3x' - y' - 3 = 0\end{array}\]
Do đó, ảnh của đường thẳng \[d:3x - y - 3 = 0\] qua phép vị tự tâm \[I\left( {2;3} \right)\] tỉ số \[k = - 1\] là đường thẳng \[d':3x - y - 3 = 0\] .
Ta tìm ảnh của đường thẳng d’ qua phép tịnh tiến theo véctơ \[\overrightarrow v \left( {1;3} \right)\].
Gọi \[N\left( {{x_1};{y_1}} \right) \in d':3x - y - 3 = 0\] và \[N'\left( {{x_2};{y_2}} \right)\] là ảnh của qua \[{T_{\overrightarrow v }}\].
Khi đó ta có: \[\left\{ \begin{array}{l}{x_2} = {x_1} + 1\\{y_2} = {y_1} + 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} = {x_2} - 1\\{y_1} = {y_2} - 3\end{array} \right. \Rightarrow N\left( {{x_2} - 1;{y_2} - 3} \right)\].
Thay tọa độ \[N\left( {{x_2} - 1;{y_2} - 3} \right)\] vào phương trình đường thẳng \[d':3x - y - 3 = 0\] ta được: \[3\left( {{x_2} - 1} \right) - \left( {{y_2} - 3} \right) - 3 = 0 \Leftrightarrow 3{x_2} - {y_2} - 3 = 0\]
Vậy ảnh của đường thẳng d’ qua phép tịnh tiến theo véctơ \[\overrightarrow v \left( {1;3} \right)\] là đường thẳng \[{d_1}:3x - y - 3 = 0\].
Hay đường thẳng cần tìm là: \[{d_1}:3x - y - 3 = 0\].
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Sử dụng kiến thức về tổ hợp và hai quy tắc đếm cơ bản.
Cách giải
TH1: Đội tuyển gồm 1 học sinh khối 10 và 9 học sinh của 2 khối 11 và khối 12.
Số cách chọn là: \[C_5^1.C_{10}^9 = 50\] cách.
TH2: Đội tuyển gồm 2 học sinh khối 10 và 8 học sinh của 2 khối 11 và khối 12.
Số cách chọn là: \[C_5^2.C_{10}^8 = 450\] cách.
Vậy có \[450 + 50 = 500\] cách chọn thỏa mãn yêu cầu đề bài.
Câu 6:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp
Sử dụng kiến thức về quy tắc nhân.
Cách giải
Tập hợp các chữ số lẻ là \[M = \left\{ {1;3;5;7;9} \right\}\]
Gọi số cần tìm là \[\overline {ab} \left( {a;b \in M} \right)\]
Khi đó a có 5 cách chọn và b có 5 cách chọn nên có \[5.5 = 25\] số thỏa mãn yêu cầu đề bài.
Câu 7:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp
Đưa phương trình về dạng cơ bản: \[\cos f\left( x \right) = \cos g\left( x \right) \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = g\left( x \right) + k2\pi \\f\left( x \right) = - g\left( x \right) + k2\pi \end{array} \right.\].
Cách giải
Ta có: \[\sin x = \cos 2x \Leftrightarrow \cos \left( {\frac{\pi }{2} - x} \right) = \cos 2x \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{2} - x + k2\pi \\2x = x - \frac{\pi }{2} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + \frac{{k2\pi }}{3}\\x = - \frac{\pi }{2} + k2\pi \end{array} \right.\].
Vì \[x \in \left( { - \pi ;\pi } \right)\] nên \[x \in \left\{ {\frac{\pi }{6};\frac{{5\pi }}{6}; - \frac{\pi }{2}} \right\}\].
Vậy có 3 nghiệm thỏa mãn đề bài.
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp
Hàm số \[y = \cos x\] có tập giá trị \[\left[ { - 1;1} \right]\].
Cách giải
Ta có tập giá trị của hàm số \[y = \cos \left( {2019x - \frac{\pi }{4}} \right)\] là \[\left[ { - 1;1} \right]\].
Câu 9:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Sử dụng: \[{\left( {1 + x} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{x^k}} \].
Thay x và n bởi các số thích hợp để xuất hiện tổng cần tìm.
Cách giải
Ta có: \[{\left( {1 + x} \right)^{2019}} = \sum\limits_{k = 0}^{2019} {C_{2019}^k{x^k}} \]
Thay \[x = 1\] ta có: \[\begin{array}{l}{2^{2019}} = \sum\limits_{k = 0}^{2019} {C_{2019}^k} = C_{2019}^0 + C_{2019}^1 + C_{2019}^2 + ... + C_{2019}^{2018} + C_{2019}^{2018}\\ \Rightarrow C_{2019}^1 + C_{2019}^2 + ... + C_{2019}^{2018} = {2^{2019}} - C_{2019}^0 - C_{2019}^{2019} = {2^{2019}} - 2\end{array}\]
Câu 10:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp
Xác định tâm I của đường tròn \[\left( C \right)\].
Sử dụng biểu thức tọa độ của phép tịnh tiến theo vectơ \[\overrightarrow v = \left( {a;b} \right)\] biến \[M\left( {x;y} \right)\] thành \[M'\left( {x';y'} \right)\] thì \[\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\].
Cách giải
Đường tròn \[\left( C \right)\] có tâm \[I\left( {0;1} \right)\].
Ảnh của \[I\left( {0;1} \right)\] qua tịnh tiến theo vectơ \[\overrightarrow v \left( {3; - 2} \right)\] là \[I'\left( {x';y'} \right)\] là tâm của đường tròn \[\left( {C'} \right)\].
Khi đó \[\left\{ \begin{array}{l}x' = 0 + 3 = 3\\y' = 1 + \left( { - 2} \right) = - 1\end{array} \right. \Rightarrow I'\left( {3; - 1} \right)\].
Câu 11:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Chia cả hai vế cho 2 sau đó sử dụng công thức \[\cos \left( {a \pm b} \right) = \cos a\cos b \mp \sin a\sin b\] và \[\sin \left( {a \pm b} \right) = \sin a\cos b \pm \cos a\sin b\].
Cách giải
Ta có: \[\sqrt 3 \sin x + \cos x = 1 \Leftrightarrow \frac{{\sqrt 3 }}{2}\sin x + \frac{1}{2}\cos x = \frac{1}{2} \Leftrightarrow \cos \frac{\pi }{3}\cos x + \sin \frac{\pi }{3}\sin x = \frac{1}{2} \Leftrightarrow \cos \left( {x - \frac{\pi }{3}} \right) = \frac{1}{2}\].
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp
Sử dụng hai quy tắc đếm cơ bản.
Cách giải
Gọi số cần tìm là \[\overline {abcd} \].
TH1: \[d = 0\] thì:
a có 5 cách chọn.
b có 4 cách chọn.
c có 3 cách chọn.
Suy ra có \[1.5.4.3 = 60\] số chẵn có chữ số tận cùng là 0.
TH2: \[d \in \left\{ {2;4} \right\}\] thì d có 2 cách chọn.
a có 4 cách chọn.
b có 4 cách chọn.
c có 3 cách chọn.
Suy ra có \[2.4.4.3 = 96\] số.
Vậy lập được tất cả \[96 + 60 = 156\] số thỏa mãn đề bài.
Câu 13:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp
Hàm số \[y = \tan x\] xác định khi \[\cos x \ne 0\]
Cách giải
Hàm số \[y = \tan x\] xác định khi \[\cos x \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi \].
Nên TXĐ: \[D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\].
Câu 14:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp
Hàm số \[y = f\left( x \right)\] xác định trên D thỏa mãn \[\left\{ \begin{array}{l}\forall x \in D \Rightarrow - x \in D\\f\left( { - x} \right) = - f\left( x \right)\end{array} \right.\] thì nó là hàm số lẻ.
Cách giải
Xét hàm số \[y = f\left( x \right) = 2x\cos 2x\] có TXĐ: \[D = \mathbb{R}\].
Nên \[\forall x \in D \Rightarrow - x \in D\].
Lại có \[f\left( { - x} \right) = 2\left( { - x} \right).\cos \left[ {2\left( { - x} \right)} \right] = - 2x\cos \left( { - 2x} \right) = - 2x\cos 2x = - f\left( x \right)\].
Nên hàm số \[y = 2x\cos 2x\] là hàm số lẻ.
Câu 15:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Sử dụng tính đơn điệu của các hàm lượng giác cơ bản.
Cách giải
Hàm số \[y = \sin x\] nghịch biến trên mỗi khoảng \[\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\].
Câu 16:
Cho các hình vẽ sau:

Trong các hình trên, hình nào có trục đối xứng và đồng thời có tâm đối xứng?
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp
Sử dụng định nghĩa hình có trục đối xứng và hình có tâm đối xứng.
Cách giải
Hình 1 vừa có trục đối xứng và tâm đối xứng.
Hình 2 và hình 3 có trục đối xứng nhưng không có tâm đối xứng.
Hình 4 có tâm đối xứng nhưng không có trục đối xứng.
Câu 17:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp
Sử dụng kiến thức về hai đường thẳng chéo nhau.
Cách giải
Khẳng định: Hai đường thẳng không có điểm chung thì chéo nhau là sai vì chúng có thể song song với nhau.
Câu 18:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Sử dụng kiến thức về cách xác định mặt phẳng trong không gian.
Cách giải
Đáp án A: Có duy nhất một mặt phẳng đi qua ba điểm phân biệt cho trước là sai vì ta cần thêm điều kiện ba điểm này không thẳng hàng.
Đáp án B: Có duy nhất một mặt phẳng đi qua hai đường thẳng cắt nhau cho trước là đúng.
Đáp án C: Có duy nhất một mặt phẳng đi qua một điểm và một đường thẳng cho trước là sai vì ta cần thêm điều kiện điểm đó nằm ngoài đường thẳng.
Đáp án D: Sai.
Câu 19:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp
Sử dụng kiến thức về phép vị tự.
Cách giải
Có duy nhất 1 phép vị tự biến \[\left( {I;R} \right)\] thành \[\left( {I';R'} \right)\].
Câu 20:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Giải phương trình lượng giác cơ bản: \[\cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \left( {k \in \mathbb{Z}} \right)\].
Cách giải
Ta có: \[\cot x = - 1 \Leftrightarrow x = - \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)\].
Câu 21:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp
Đếm số cách chọn \[\overline {abcdef} \] thỏa mãn \[a < b < c < d < e < f\].
Cách giải
Gọi số thỏa mãn bài toán là \[\overline {abcdef} \] với \[0 < a < b < c < d < e < f \le 9\]
NX: Mỗi cách chọn một bộ 6 chữ số \[a,b,c,d,e,f\] thì chỉ có 1 cách sắp xếp duy nhất sao cho \[a < b < c < d < e < f\].
Do đó mỗi số thỏa mãn bài toán là một tổ hợp chập 6 của 9 phần tử 1; 2;…; 9.
Số các số cần tìm là \[C_9^6\].
Câu 22:
Cho tứ diện ABCD có \[AB = BC = AC = CD = DB = a,AD = \frac{{a\sqrt 3 }}{2}\]. Gọi M là trung điểm của AB, điểm O là tâm đường tròn ngoại tiếp tam giác BCD. Đường thẳng AO cắt mặt phẳng \[\left( {MCD} \right)\] tại G. Tính diện tích tam giác GAD.
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Tính độ dài các đoạn GA, GD, AD rồi nhận xét tính chất tam giác GAD.
Cách giải
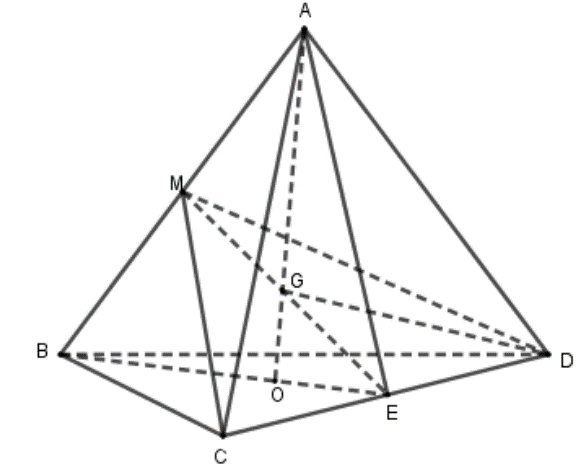
Tam giác ACD có \[AC = CD = a,AD = \frac{{a\sqrt 3 }}{2}\] nên \[A{E^2} = \frac{{A{C^2} + A{D^2}}}{2} - \frac{{C{D^2}}}{4} = \frac{{{a^2} + \frac{{3{a^2}}}{4}}}{2} - \frac{{{a^2}}}{4} = \frac{{5{a^2}}}{8}\].
Tam giác BCD đều \[ \Rightarrow BE = \frac{{a\sqrt 3 }}{2}\].
Tam giác ABE có EM là đường trung tuyến của tam giác AEB nên:
\[E{M^2} = \frac{{E{A^2} + E{B^2}}}{2} - \frac{{A{B^2}}}{4} = \frac{{\frac{{5{a^2}}}{8} + \frac{{3{a^2}}}{4}}}{2} - \frac{{{a^2}}}{4} = \frac{{7{a^2}}}{{16}}\].
Xét tam giác BME và bộ ba điểm A, G, O thẳng hàng có: \[\frac{{AM}}{{AB}}.\frac{{OB}}{{OE}}.\frac{{GE}}{{GM}} = 1 \Rightarrow \frac{1}{2}.2.\frac{{GE}}{{GM}} = 1 \Leftrightarrow \frac{{GE}}{{GM}} = 1\] hay G là trung điểm của ME.
Xét tam giác ABD có DM là trung tuyến của \[\Delta ABD\] nên \[D{M^2} = \frac{{D{A^2} + B{D^2}}}{2} - \frac{{A{B^2}}}{4} = \frac{{5{a^2}}}{8}\].
Tam giác DME có trung tuyến DG nên \[D{G^2} = \frac{{D{E^2} + D{M^2}}}{2} - \frac{{M{E^2}}}{4} = \frac{{\frac{{{a^2}}}{4} + \frac{{5{a^2}}}{8}}}{2} - \frac{{7{a^2}}}{{64}} = \frac{{21{a^2}}}{{64}}\].
Lại có: \[\begin{array}{l}\cos AEM = \frac{{A{E^2} + E{M^2} - A{M^2}}}{{2.AE.EM}} = \frac{{\frac{{5{a^2}}}{8} + \frac{{7{a^2}}}{{16}} - \frac{{{a^2}}}{4}}}{{2.\sqrt {\frac{{5{a^2}}}{8}.\frac{{7{a^2}}}{{16}}} }} = \frac{{13}}{{2\sqrt {70} }}\\ \Rightarrow A{G^2} = A{E^2} + E{G^2} - 2AE.EG.\cos AEG = \frac{{5{a^2}}}{8} + \frac{{7{a^2}}}{{64}} - 2.\sqrt {\frac{{5{a^2}}}{8}.\frac{{7{a^2}}}{{64}}} .\frac{{13}}{{2\sqrt {70} }} = \frac{{21{a^2}}}{{64}}\end{array}\]
Tam giác ADG có \[A{G^2} = \frac{{21{a^2}}}{{64}},A{D^2} = \frac{{3{a^2}}}{4},D{G^2} = \frac{{21{a^2}}}{{64}}\].
Do đó \[\Delta GAD\] cân tại G.
Gọi H là trung điểm của AD thì \[AH = \frac{{a\sqrt 3 }}{4},G{H^2} = G{A^2} - A{H^2} = \frac{{21{a^2}}}{{64}} - \frac{{3{a^2}}}{{16}} = \frac{{9{a^2}}}{{64}} \Rightarrow GH = \frac{{3a}}{8}\].
Diện tích tam giác \[{S_{GAD}} = \frac{1}{2}.GH.AD = \frac{1}{2}.\frac{{3a}}{8}.\frac{{a\sqrt 3 }}{2} = \frac{{3{a^2}\sqrt 3 }}{{32}}\].
Câu 23:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
- Đếm số cách chọn 15 trong 25 câu để làm đúng.
- Tính xác suất để làm đúng một câu.
- Dùng quy tắc nhân xác suất.
Cách giải
Xác suất để làm đúng một câu là \[\frac{1}{4}\], xác suất để làm sai một câu là \[\frac{3}{4}\].
Chọn 15 trong 25 câu để làm đúng có \[C_{25}^{15}\] cách chọn.
Xác suất cần tìm là: \[C_{25}^{15}.{\left( {\frac{1}{4}} \right)^{15}}.{\left( {\frac{3}{4}} \right)^{10}} = \frac{{{3^{10}}.C_{25}^{15}}}{{{4^{25}}}}\].
Câu 24:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp
Đặt \[t = \sin x - \cos x\] tính \[\sin x\cos x = \frac{{1 - {t^2}}}{2}\] thay vào phương trình.
Giải phương trình và kết luận.
Cách giải
Đặt \[t = \sin x - \cos x\left( { - \sqrt 2 \le t \le \sqrt 2 } \right)\] thì \[{t^2} = 1 - 2\sin x\cos x \Leftrightarrow \sin x\cos x = \frac{{1 - {t^2}}}{2}\].
Thay vào phương trình ta được \[\begin{array}{l}\left| t \right| + 8.\frac{{1 - {t^2}}}{2} = 1 \Leftrightarrow 2\left| t \right| + 8 - 8{t^2} = 2 \Leftrightarrow 8{t^2} - 2\left| t \right| - 6 = 0\\ \Leftrightarrow \left[ \begin{array}{l}\left| t \right| = 1\\\left| t \right| = - \frac{3}{4}\left( {VN} \right)\end{array} \right. \Leftrightarrow t = \pm 1\left( {TM} \right)\end{array}\]
TH1: \[t = 1\] thì \[\begin{array}{l}\sin x - \cos x = 1 \Leftrightarrow \sqrt 2 \sin \left( {x - \frac{\pi }{4}} \right) = 1 \Leftrightarrow \sin \left( {x - \frac{\pi }{4}} \right) = \frac{1}{{\sqrt 2 }}\\ \Leftrightarrow \left[ \begin{array}{l}x - \frac{\pi }{4} = \frac{\pi }{4} + k2\pi \\x - \frac{\pi }{4} = \frac{{3\pi }}{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{2} + k2\pi \\x = \pi + k2\pi \end{array} \right.\end{array}\]
TH2: \[\begin{array}{l}\sin x - \cos x = - 1 \Leftrightarrow \sqrt 2 \sin \left( {x - \frac{\pi }{4}} \right) = - 1 \Leftrightarrow \sin \left( {x - \frac{\pi }{4}} \right) = - \frac{1}{{\sqrt 2 }}\\ \Leftrightarrow \left[ \begin{array}{l}x - \frac{\pi }{4} = - \frac{\pi }{4} + k2\pi \\x - \frac{\pi }{4} = \frac{{5\pi }}{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k2\pi \\x = \frac{{3\pi }}{2} + k2\pi \end{array} \right.\end{array}\]
Vậy có bốn điểm biểu diễn nghiệm của phương tình trên đường tròn lượng giác.
Câu 25:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp
Tìm số hạng tổng quát trong khai triển, đánh giá tìm số hạng lớn nhất.
Cách giải
SHTQ: \[{T_{k + 1}} = C_{10}^k.{\left( {\frac{1}{3}} \right)^{10 - k}}.{\left( {\frac{2}{3}x} \right)^{10 - k}} = C_{10}^k.\frac{1}{{{3^{10 - k}}}}.\frac{{{2^k}}}{{{3^k}}}.{x^k} = \frac{{C_{10}^k{{.2}^k}}}{{{3^{10}}}}.{x^k}\].
Hệ số của SHTQ là \[\frac{{C_{10}^k{{.2}^k}}}{{{3^{10}}}}\].
Ta có: \[\begin{array}{l}\frac{{C_{10}^k{{.2}^k}}}{{{3^{10}}}} < \frac{{C_{10}^{k + 1}{{.2}^{k + 1}}}}{{{3^{10}}}} \Leftrightarrow C_{10}^k{.2^k} < C_{10}^{k + 1}{.2^{k + 1}} \Leftrightarrow C_{10}^k < 2C_{10}^{k + 1} \Leftrightarrow \frac{{10!}}{{k!\left( {10 - k} \right)!}} < 2.\frac{{10!}}{{\left( {k + 1} \right)!\left( {9 - k} \right)!}}\\ \Leftrightarrow \frac{1}{{10 - k}} < \frac{2}{{k + 1}} \Leftrightarrow k + 1 < 2\left( {10 - k} \right) \Leftrightarrow 3k < 19 \Leftrightarrow k < \frac{{19}}{3}\end{array}\]
Do đó: \[\frac{{C_{10}^0{{.2}^0}}}{{{3^{10}}}} < \frac{{C_{10}^1{{.2}^1}}}{{{3^{10}}}} < ... < \frac{{C_{10}^6{{.2}^6}}}{{{3^{10}}}}\] và \[\frac{{C_{10}^7{{.2}^7}}}{{{3^{10}}}} > \frac{{C_{10}^7{{.2}^7}}}{{{3^{10}}}} > ... > \frac{{C_{10}^{10}{{.2}^{10}}}}{{{3^{10}}}}\]
Mà \[\frac{{C_{10}^6{{.2}^6}}}{{{3^{10}}}} < \frac{{C_{10}^7{{.2}^7}}}{{{3^{10}}}}\] nên hệ số lớn nhất là \[\frac{{C_{10}^7{{.2}^7}}}{{{3^{10}}}}\].
Câu 26:
 Xem đáp án
Xem đáp án
Phương pháp
a)
- Xét \[\cos x = 0\] thay vào phương trình và kiểm tra.
- Xét \[\cos x \ne 0\] và chia cả hai vế của phương trình cho \[{\cos ^2}x \ne 0\] đưa về phương trình bậc hai ẩn \[\tan x\].
- Giải phương trình và kết luận nghiệm.
Cách giải
a) Giải phương trình: \[{\sin ^2}x + 2\sqrt 3 \sin x\cos x - {\cos ^2}x = - 2\].
+) Xét \[\cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi \]. Khi đó \[{\sin ^2}x = 1 - {\cos ^2}x = 1\], thay vào phương trình ta được: \[1 + 0 - 0 = - 2 \Leftrightarrow 1 = - 2\] (vô lí).
Suy ra \[x = \frac{\pi }{2} + k\pi ;k \in \mathbb{Z}\] không phải là nghiệm.
+) Xét \[\cos x \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi ;k \in \mathbb{Z}\], chia hai vế của phương trình cho \[{\cos ^2}x \ne 0\] ta được:
\[\begin{array}{l}\frac{{{{\sin }^2}x}}{{{{\cos }^2}x}} + \frac{{2\sqrt 3 \sin x\cos x}}{{{{\cos }^2}x}} - \frac{{{{\cos }^2}x}}{{{{\cos }^2}x}} = - \frac{2}{{{{\cos }^2}x}} \Leftrightarrow {\tan ^2}x + 2\sqrt 3 \tan x - 1 = - 2\left( {1 + {{\tan }^2}x} \right)\\ \Leftrightarrow 3{\tan ^2}x + 2\sqrt 3 \tan x + 1 = 0 \Leftrightarrow \tan x = - \frac{{\sqrt 3 }}{3} \Leftrightarrow x = \frac{{ - \pi }}{6} + k\pi ,k \in \mathbb{Z}\end{array}\]
Câu 27:
 Xem đáp án
Xem đáp án
b) Đặt \[u = \sqrt {\cos x + m} \] đưa về hệ phương trình.
Tìm m để hệ có nghiệm và kết luận.
Cách giải
b) Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm: \[{\cos ^2}x + \sqrt {\cos x + m} = m\].
Đặt \[u = \sqrt {\cos x + m} \], ta có hệ \[\left\{ \begin{array}{l}{\cos ^2}x + u = m\\{u^2} - \cos x = m\end{array} \right.\]. Trừ vế theo vế ta được:
\[{\cos ^2}x - {u^2} + u + \cos x = 0 \Leftrightarrow \left( {u + \cos x} \right)\left( {\cos x - u + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}u = - \cos x\\u = \cos x + 1\end{array} \right.\].
\[*)\;u = \cos x + 1\], ta được \[\sqrt {m + \cos x} = \cos x + 1\;\;\;\left( 1 \right)\].
\[\left( 1 \right) \Leftrightarrow m + \cos x = {\left( {\cos x + 1} \right)^2} \Leftrightarrow m = {\cos ^2}x + \cos x + 1\].
Đặt \[t = \cos x\left( { - 1 \le t \le 1} \right)\] ta được \[m = {t^2} + t + 1 = f\left( t \right)\].
Bảng biến thiên:
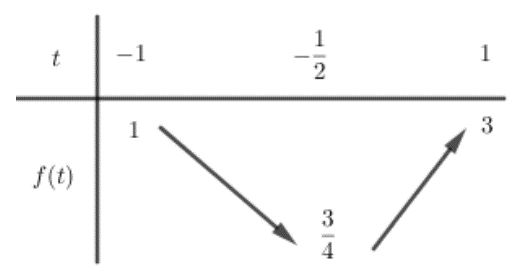
Phương trình có nghiệm \[ \Leftrightarrow \frac{3}{4} \le m \le 3\].
\[*)\;u = - \cos x\], ta được \[\sqrt {m + \cos x} = - \cos x \Leftrightarrow \left\{ \begin{array}{l} - \cos x \ge 0\\m + \cos x = {\cos ^2}x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\cos x \le 0\\m = {\cos ^2}x - \cos x\end{array} \right.\].
Đặt \[t = \cos x\left( { - 1 \le t \le 0} \right)\] ta được: \[m = {t^2} - t\]
Xét hàm số \[g\left( t \right) = {t^2} - t\] trong đoạn \[\left[ { - 1;0} \right]\] ta có bảng biến thiên:
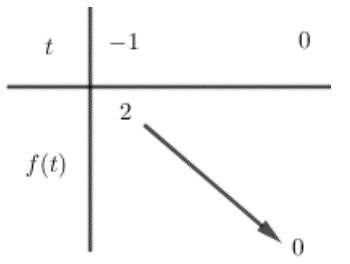
Phương trình có nghiệm \[ \Leftrightarrow 0 \le m \le 2\].
Kết hợp với TH1 ta được \[0 \le m \le 3\].
Vậy \[m \in \left[ {0;3} \right]\].
Câu 28:
 Xem đáp án
Xem đáp án
Phương pháp
- Tính số phần tử của không gian mẫu.
- Tính số khả năng có lợi cho biến cố.
- Tính xác suất theo công thức \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\].
Cách giải
Chọn 3 trong 11 học sinh có \[n\left( \Omega \right) = C_{11}^3 = 165\].
Gọi A là biến cố: “3 học sinh được chọn có cả nam và nữ”.
TH1: Chọn 1 bạn nam và 2 bạn nữ có \[C_2^1.C_9^2 = 72\] cách.
TH2: Chọn 2 bạn nam và 1 bạn nữ có \[C_2^2.C_9^1 = 9\] cách.
Suy ra \[n\left( A \right) = 72 + 9 = 81 \Rightarrow P\left( A \right) = \frac{{81}}{{165}} = \frac{{27}}{{55}}\].
Câu 29:
Cho hình chóp S.ABCD có đáy ABCD là hình thang \[\left( {AB//CD,AB = 2CD} \right)\]. Gọi M là trung điểm của cạnh SC.
a) Xác định giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\].
b) Xác định giao điểm K của đường thẳng AM với \[mp\left( {SBD} \right)\]. Tính tỉ số \[\frac{{AK}}{{AM}}\].
 Xem đáp án
Xem đáp án
Phương pháp
a) Sử dụng định lí \[\left\{ \begin{array}{l}a \subset \left( P \right)\\b \subset \left( Q \right)\\\left( P \right) \cap \left( Q \right) = d\\a//b\end{array} \right. \Rightarrow d//a//b\]
b) Phương pháp xác định giao điểm của đường thẳng với mặt phẳng:
- Tìm mặt phẳng phụ \[\left( P \right)\] chứa đường thẳng a.
- Tìm giao tuyến d của \[\left( P \right)\] với \[\left( \alpha \right)\] đã cho.
- Tìm giao điểm của d với a.
Sử dụng định lí Ta-let suy ra tỉ số.
Cách giải
a) Xác định giao tuyến của hai mặt phẳng \[\left( {{\bf{SAB}}} \right)\] và \[\left( {{\bf{SCD}}} \right)\].
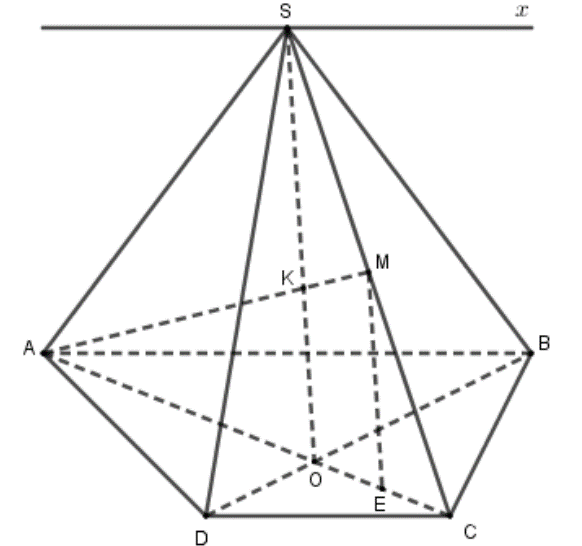
S là điểm chung của \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\].
\[AB//CD;AB \subset \left( {SAB} \right);CD \subset \left( {SCD} \right)\].
Suy ra \[\left( {SAB} \right) \cap \left( {SCD} \right) = Sx//AB//CD\].
b) Xác định giao điểm K của đường thẳng AM với \[{\bf{mp}}\left( {{\bf{SBD}}} \right)\]. Tính tỉ số \[\frac{{{\bf{AK}}}}{{{\bf{AM}}}}\].
Ta có: \[AM \subset \left( {SAC} \right)\]
Dễ thấy \[S \in \left( {SAC} \right) \cap \left( {SBD} \right)\].
Gọi O là giao điểm của AC và BD. Khi đó \[O \in AC \subset \left( {SAC} \right),O \in BD \subset \left( {SBD} \right)\] nên \[O \in \left( {SAC} \right) \cap \left( {SBD} \right)\]
Do đó \[SO = \left( {SAC} \right) \cap \left( {SBD} \right)\]
Trong \[\left( {SAC} \right)\], gọi \[K = AM \cap SO\] thì \[K \in AM,K \in SO \subset \left( {SBD} \right)\] nên \[K = AM \cap \left( {SBD} \right)\].
Do \[AB//CD\] nên \[\frac{{OC}}{{OA}} = \frac{{CD}}{{AB}} = \frac{1}{2} \Rightarrow OA = \frac{2}{3}AC,OC = \frac{1}{3}AC\].
Gọi E là trung điểm của OC suy ra ME là đường trung bình của \[\Delta SCO \Rightarrow ME//SO\].
Mà \[OE = \frac{1}{2}OC = \frac{1}{2}.\frac{1}{3}.AC = \frac{1}{6}.AC \Rightarrow AE = AO + OE = \frac{2}{3}AC + \frac{1}{6}AC = \frac{5}{6}AC\].
\[ \Rightarrow \frac{{AK}}{{AM}} = \frac{{AO}}{{AE}} = \frac{4}{5}\].
