Tính diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số .
A.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
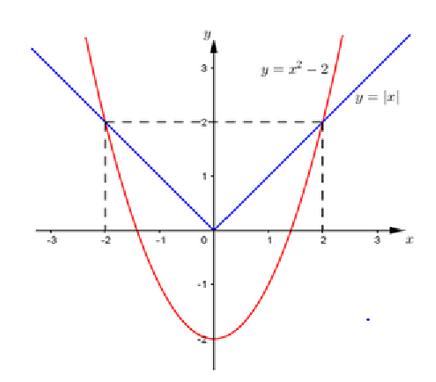
Dựa vào đồ thị hàm số ta có:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(3;2;-1) và đi qua điểm A(2;1;2). Mặt phẳng nào dưới đây tiếp xúc với (S) tại A?
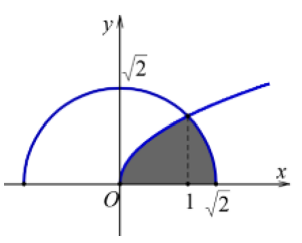
Cho (H) là hình phẳng giới hạn bởi đường cong có phương trình , nửa đường tròn có phương trình (với ) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của hình (H) bằng:
Trong không gian với hệ tọa độ Oxyz, cho . Gọi G là trọng tâm tam giác ABC. Biết điểm M nằm trên mặt phẳng (Oxy) sao cho độ dài đoạn thẳng GM ngắn nhất. Tính độ dài đoạn thẳng GM.
Cho ba số phức phân biệt thỏa mãn và . Biết lần lượt được biểu diễn bởi các điểm A, B, C trên mặt phẳng phức. Tính góc .
Trong không gian với hệ tọa độ Oxyz, gọi là mặt phẳng cắt ba trục tọa độ tại ba điểm. Phương trình mặt phẳng là:
Trong không gian Oxyz, cho hai mặt phẳng . Gọi (S) là mặt cầu có tâm thuộc (Q) và cắt (P) theo giao tuyến là đường tròn có tâm E(-1;2;3), bán kính r = 8. Phương trình mặt cầu (S) là:
Trong không gian Oxyz, cho ba điểm . Gọi là các mặt cầu có tâm A, B, C và bán kính lần lượt bằng 3, 2, 3. Hỏi có bao nhiêu mặt phẳng qua điểm và tiếp xúc với cả 3 mặt cầu .
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;-2;3) và B(5;4;7). Phương trình mặt cầu nhận AB làm đường kính là:
Với số phức z thỏa mãn , tập hợp các điểm biểu diễn các số phức z là một đường tròn. Tìm bán kính R của đường tròn đó.
Cho các số phức . Tập giá trị tham số m để số phức có môđun nhỏ nhất trong ba số phức đã cho là:
Thể tích của khối tròn xoay sinh ra khi cho hình phẳng giới hạn bởi Parabol và đường thẳng d: y = x xoay quanh trục Ox bằng: