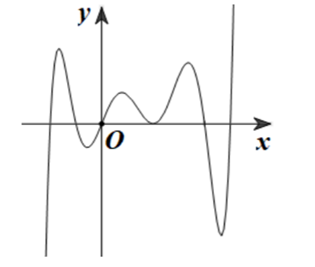
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) liên tục trên \(\mathbb{R}\)và đồ thị của \(f'\left( x \right)\) như hình vẽ
 Giải bởi Vietjack
Giải bởi Vietjack
Cho hàm số \(f\left( x \right) = \frac{{(m + 1)x + 4}}{{x + 2m}}\) (\(m\) là tham số thực). Có bao nhiêu giá
trị nguyên \(m\) để hàm số nghịch biến trên khoảng \(\left( {0; + \infty } \right)\)?