Cho vuông tại A có . Quay xung quanh cạnh AB, đường gấp khúc ACB tạo nên một hình nón tròn xoay. Diện tích xung quanh của hình nón đó là
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Khi quay tam giác ABC vuông tại A quanh cạnh AB ta được hình nón có chiều cao AB, bán kính đáy AC và đường sinh BC.
Ta có:
Diện tích xung quanh của hình nón tạo thành là: .
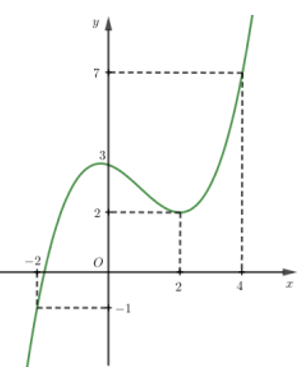
Cho hàm số y =f(x) có đạo hàm trên R và có đồ thị như hình vẽ sau. Số nghiệm nguyên của phương trình là
![Cho hàm số y =f(x) có đạo hàm trên R và có đồ thị như hình vẽ sau. Số nghiệm nguyên của phương trình ([f(x^2 -2)^2 ])^t =0 là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/02/blobid11-1676552501.png)
Cho hàm số y =f(x) liên tục trên R đồng thời thỏa mãn điều kiện và . Hàm số nghịch biến trên khoảng nào?
Đồ thị (C) của hàm số cắt trục Oy tại điểm M. Tiếp tuyến của đồ thị (C) tại M có phương trình là
Cho khối nón có chiều cao h =9a và bán kính đường tròn đáy r = 2a. Thể tích của khối nón đã cho là
Cho hình chữ nhật ABCD có . Gọi M, N lần lượt là trung điểm của AD, BC. Khối trụ tròn xoay tạo thành khi quay hình chữ nhật ABCD (kể cả điểm trong) xung quanh cạnh MN có thể tích bằng bao nhiêu?
Cho hàm số y =f(x) liên tục trên R và có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số . Giá trị của biểu thức 2M + 3m bằng
Cắt khối nón bởi một mặt phẳng qua trục, thiết diện là một tam giác đều có diện tích bằng . Thể tích của khối nón đó bằng
Cho hình chóp S.ABC có đáy ABCD là hình thoi, . Tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Khoảng cách giữa hai đường thẳng BD và SC bằng
Cho hình chóp S.ABC có , ABCD là hình chữ nhật, . Thể tích khối chóp S.ABCD bằng
Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông tại A. Biết AA' và AC =2a. Thể tích của khối lăng trụ ABC.A'B'C' là
Cho khối trụ có chiều cao h = 4a và bán kính đường tròn đáy r = 2a. Thể tích của khối trụ đã cho bằng