D. \(5\left( {cm} \right)\)
Giải bởi Vietjack
Đáp án A
Phương pháp:
Lập hàm số tính thể tích khối hộp theo biến x, khảo sát tìm x để hộp nhận được có thể tích lớn nhất.
Cách giải:
Sau khi cắt, độ dài 2 chiều của đáy là: \(40 - 2x,\,\,\,\frac{{60 - 3x}}{2}\left( {cm} \right),\,\,x \in \left( {0;20} \right)\)
Thể tích khối hộp: \(V = x\left( {40 - 2x} \right).\frac{{60 - 3x}}{2} = 3x{\left( {20 - x} \right)^2} = f\left( x \right)\)
\(f'\left( x \right) = 3{\left( {20 - x} \right)^2} - 3x.2\left( {20 - x} \right) = 3 = 3.\left( {20 - x} \right)\left( {20 - 3x} \right)\)
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 20\left( L \right)\\x = \frac{{20}}{3}\end{array} \right.\)
Bảng biến thiên:
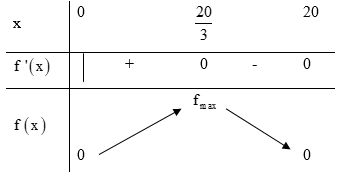
Vậy \(x = \frac{{20}}{3}\) thì hộp nhận được có thể tích lớn nhất.
Tính tích các nghiệm của phương trình \({\log _2}x.{\log _4}x.{\log _8}x.{\log _{16}}x = \frac{{81}}{{24}}\)
Cho a, b là hai số dương khác 1. Đặt \({\log _a}b = m\). Tính theo m giá trị của biểu thức \(P = {\log _a}b - {\log _{\sqrt b }}{a^3}\)
Tìm tập nghiệm của bất phương trình \({\log _x}125x + {\log _{24}}x > \frac{3}{2} + \log _5^2x\)
Cho các số thực \(a,\,b,\,x > 0\) và \(b,\,x \ne 1\) thỏa mãn \({\log _x}\frac{{a + 2b}}{3} = {\log _x}\sqrt a + {\log _x}\sqrt b \). Tính giá trị của biểu thức \(P = \left( {2{a^2} + 3ab + {b^2}} \right){\left( {a + 2b} \right)^{ - 2}}\) khi \(a > b\)
Tìm tất cả các giá trị của tham số m để hàm số \(y = {\left( {\frac{2}{\pi }} \right)^{{x^3} + 3m{x^2} + 3mx + 10}}\) nghịch biến trên khoảng \(\left( {0; + \infty } \right)\)
Tìm tất cả các giá trị thực của tham số m để phương trình \({\log _2}\left( {{5^x} - 1} \right).{\log _4}\left( {{{2.5}^x}} \right) - 2 = m\) có nghiệm \(x \ge 1\)
Hàm số \(y = \left( {{x^2} - 2x + 1} \right){e^{2x}}\) nghịch biến trên khoảng nào sau đây?
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng \(a\sqrt 3 \), góc \(ASB = {60^0}\). Tính thể tích của khối nón đỉnh S có đáy là đường tròn ngoại tiếp tứ giác ABCD.
Tìm số đường tiệm cận của đồ thị hàm số \(y = \frac{{5x + 11}}{{\sqrt {3{x^2} + 2017} }}\)
Ông A vay ngân hàng 300 triệu đồng để mua nhà theo phương thức trả góp với lãi suất 0,5% mỗi tháng. Nếu cuối mỗi tháng, bắt đầu từ tháng thứ nhất ông hoàn nợ cho ngân hàng 4.500.000 đồng và chịu lãi số tiền chưa trả. Hỏi sau bao nhiêu tháng ông A sẽ trả hết số tiền vay?
Tìm giá trị cực tiểu \({y_{CT}}\) của hàm số \(y = - {x^4} + 2{x^2} + 2\)
Tính giá trị nhỏ nhất M của hàm số \(y = - {x^3} + 3{x^2} + 2\) trên đoạn \(\left[ {1;3} \right]\)
Tìm tất cả các giá trị thực của tham số m để đường thẳng \(y = - mx\) cắt đồ thị hàm số \(y = {x^3} - 3{x^2} - m + 2\) tại ba điểm A, B, C phân biệt sao cho \(AB = BC\).
