Chọn mệnh đề đúng trong các mệnh đề sau?
A. Hình có đáy là hình bình hành thì có mặt cầu ngoại tiếp.
B. Hình chóp có đáy là hình thang vuông thì có mặt cầu ngoại tiếp.
D. Hình có đáy là hình tứ giác thì có mặt cầu ngoại tiếp.
Giải bởi Vietjack
Đáp án C
Phương pháp:
Đường tròn ngoại tiếp khối đa diện là đường tròn đi qua tất cả các đỉnh của khối đa diện đó.
Cách giải:
Trong các hình: hình bình hành, hình thang vuông, hình thang cân, hình tứ giác chỉ có hình thang cân là có đường tròn ngoại tiếp nên ta chọn C.
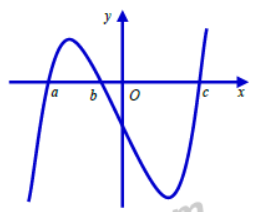
Cho hàm số \(y = f\left( x \right)\) có đạo hàm là hàm số liên tục trên R với đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ. Biết \(f\left( a \right) > 0\), hỏi đồ thị hàm số \(y = f\left( x \right)\) cắt trục hoành tại nhiều nhất bao nhiêu điểm?
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số \(y = \left( {1 - m} \right){x^4} + 2\left( {m + 3} \right){x^2} + 1\) có đúng một điểm cực tiểu và không có điểm cực đại?
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {x^3} - 3{x^2} - 9x + 1\) trên đoạn \(\left[ {0;4} \right]\). Ta có \(m + 2M\) bằng:
Hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x - 1\) nghịch biến trên khoảng nào trong các khoảng sau đây?
Rút gọn biểu thức \(A = {a^{4{{\log }_{{a^2}}}3}}\) với \(0 < a \ne 1\) ta được kết quả là
Khoảng cách giữa hai điểm cực trị của đồ thị hàm số \(y = {x^3} + 3{x^2} - 4\) là
Số điểm chung của đồ thị hàm số \(y = {x^3} - 2{x^2} + x - 12\) với trục là Ox
Rút gọn biểu thức \(A = \frac{{\sqrt[3]{{{a^5}}}.{a^{\frac{7}{3}}}}}{{{a^4}.\sqrt[7]{{{a^{ - 2}}}}}}\) với \(a > 0\) ta được kết quả \(A = {a^{\frac{m}{n}}}\), trong đó \(m,\,n \in \mathbb{N}*\) và \(\frac{m}{n}\) là phân số tối giản. Khẳng định nào sau đây đúng?
Đồ thị hàm số \(y = \frac{{\sqrt {1 - {x^2}} }}{{{x^2} + 2x}}\) có tất cả bao nhiêu tiệm cận đứng?
Giá trị lớn nhất của hàm số \(y = {x^3} - 3x + 5\) trên đoạn \(\left[ {0;\frac{3}{2}} \right]\)
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Biết \(OA = a,\,\,OB = 2a\) , và đường thẳng AC tạo với mặt phẳng \(\left( {OBC} \right)\) một góc \({60^0}\). Thể tích khối tứ diện OABC bằng
Tìm tất cả các giá trị thực của x thỏa mãn đẳng thức \({\log _3}x = 3{\log _3}2 + {\log _9}25 - {\log _{\sqrt 3 }}3\)
Cho \(0 < a \ne 1\) và \(b \in R\). Chọn mệnh đề sai trong các mệnh đề sau:
Gọi \({m_0}\) là giá trị thực của tham số để đồ thị hàm số \(y = {x^4} + 2m{x^2} + 4\) có 3 điểm cực trị nằm trên các trục tọa độ. Khẳng định nào sau đây là đúng?
