Giải bởi Vietjack
Lời giải
Chọn C
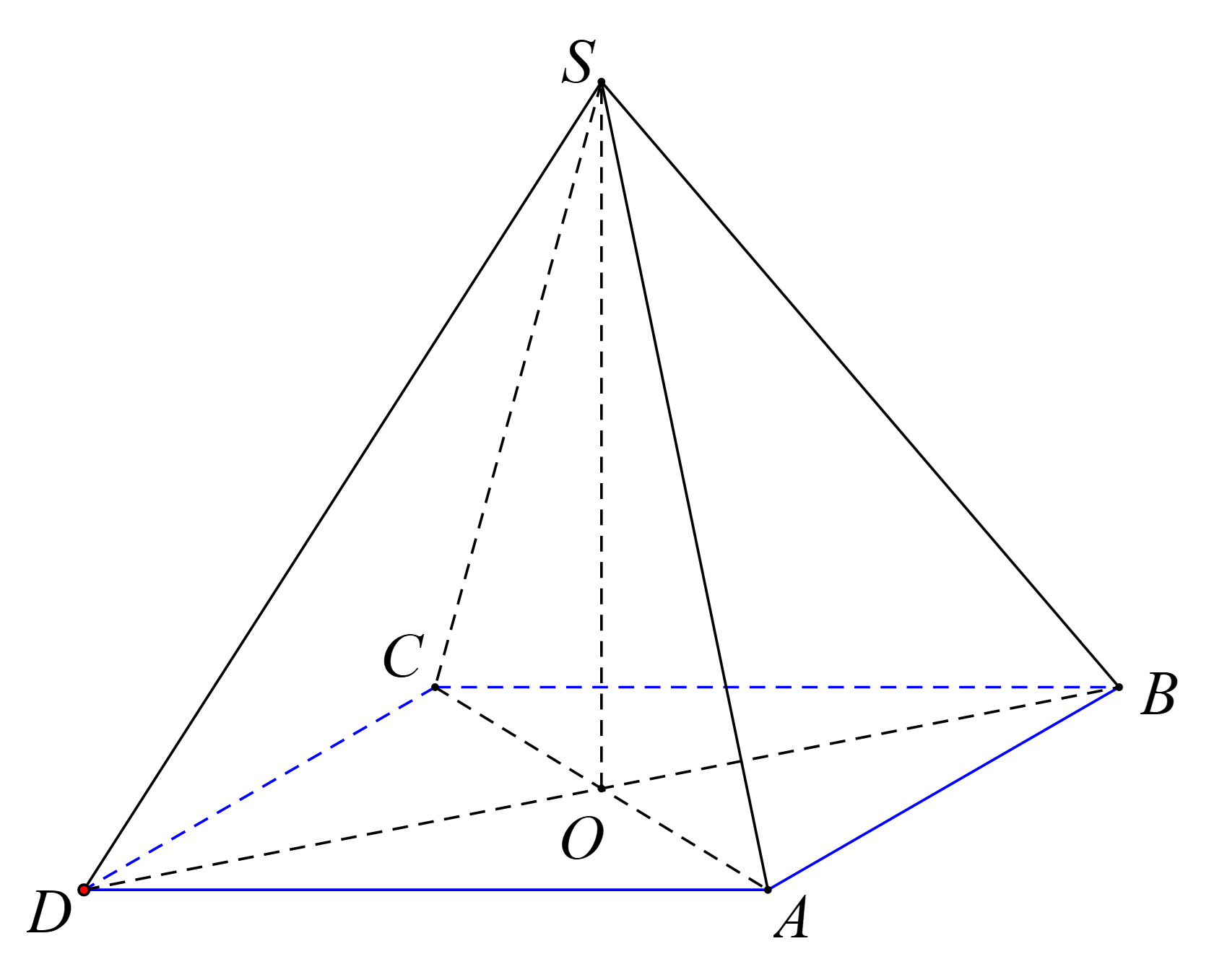
Từ giả thiết suy ra \[\widehat {\left( {SA,BC} \right)} = \widehat {\left( {SA,AD} \right)} = \widehat {SAD} = 60^\circ \]
Khi đó hình chóp có tất cả cạnh đều bằng \(6\).
Suy ra \(SO = \frac{1}{2}AC = \frac{1}{2}.6\sqrt 2 = 3\sqrt 2 \).
Nên \({V_{SABCD}} = \frac{1}{3}.36.3\sqrt 2 = 36\sqrt 2 \).
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đạo hàm là hàm số \(y = f'\left( x \right)\) với đồ thị như hình vẽ bên.
Biết rằng đồ thị hàm số \(y = f\left( x \right)\) tiếp xúc với trục hoành tại điểm có hoành độ âm. Khi đó đồ thị hàm số cắt trục tung tại điểm có tung độ là bao nhiêu?
