Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Chọn D
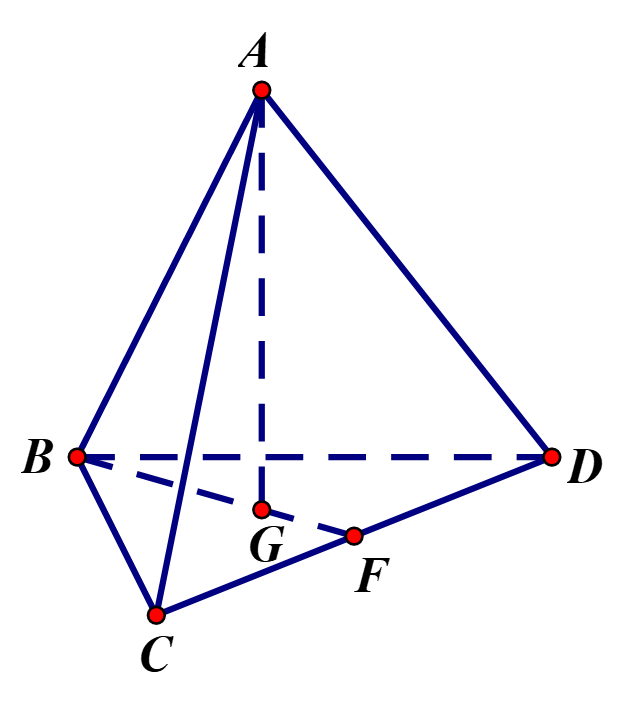
Cho \(ABCD\) là tứ diện đều.
Gọi \(F\)là trung điểm \(CD\), \(G\)là tâm của tam giác đều \(BCD\), ta có \(AG \bot \left( {BCD} \right)\).
\(BF = \sqrt {B{C^2} - C{F^2}} = \frac{{3\sqrt 3 }}{2}\).
Xét tam giác \(ABG\) vuông tại \(G\):
\(AB = 3\),\(BG = \frac{2}{3}BF = \frac{2}{3}.\frac{{3\sqrt 3 }}{2} = \sqrt 3 \)\( \Rightarrow AG = \sqrt {A{B^2} - B{G^2}} = \sqrt {{3^2} - {{\left( {\sqrt 3 } \right)}^2}} = \sqrt 6 \).
Có \({S_{BCD}} = \frac{1}{2}BF.CD = \frac{{{3^2}\sqrt 3 }}{4} = \frac{{9\sqrt 3 }}{4}\).
Vậy \({V_{ABCD}} = \frac{1}{3}AG.{S_{BCD}} = \frac{1}{3}.\sqrt 6 .\frac{{9\sqrt 3 }}{4} = \frac{{9\sqrt 2 }}{4}\).