Cho hàm số \(y = f\left( x \right)\)liên tục trên \(\mathbb{R}\backslash \left\{ 1 \right\}\)và có bảng biến thiên như sau:

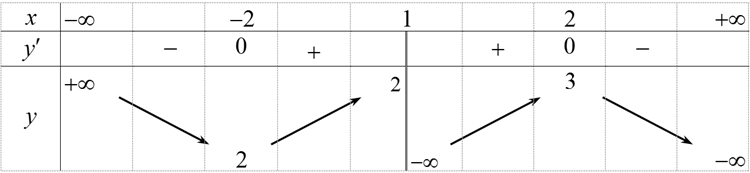
Đồ thị hàm số \(y = \frac{1}{{2f\left( x \right) - 5}}\)có bao nhiêu đường tiệm cận đứng?

Một căn bệnh có 2% dân số mắc phải. Một phương pháp được phát triển có tỉ lệ chính xác là 99%. Với những người mắc bệnh, phương pháp này sẽ đưa ra kết quả dương tính 99% số trường hợp mắc bệnh. Với những người không mắc bệnh, phương pháp này cũng chuẩn đoán đúng 99 trong 100 trường hợp. Nếu một người kiểm tra và kết quả là dương tính (bị bệnh), xác suất để người đó thực sự bị bệnh là bao nhiêu?

Có hai lô sản phẩm. Lô I có 20 sản phẩm, trong đó có 15 sản phẩm tốt và 5 sản phẩm lỗi. Lô II có 20 sản phẩm, trong đó có 10 sản phẩm tốt và 10 sản phẩm lỗi. Lấy ngẫu nhiên 1 lô và từ lô nãy lấy ngẫu nhiên ra 1 sản phẩm. Khi đó:

a) Xác suất để sản phẩm lấy ra là sản phẩm tốt bằng \(\frac{5}{8}.\)

b) Xác suất để sản phẩm lấy ra là sản phẩm lỗi bằng \(\frac{3}{8}.\)

c) Giả sử sản phẩm lấy ra là sản phẩm tốt. Xác suất để sản phẩm đó có lô thứ II là \(\frac{2}{5}.\)

d) Giả sử sản phẩm lấy ra là phế phẩm. Xác suất để sản phẩm đó có lô thứ nhất là \(\frac{1}{2}.\)

Số mệnh đề đúng trong các mệnh đề trên là

Một trường có tỉ lệ học sinh nữ là 52%. Tỉ lệ học sinh nữ và tỉ lệ học sinh tham gia câu lạc bộ nghệ thuật lần lượt là 18% và 15%. Gặp ngẫu nhiên một học sinh của trường. Biết rằng học sinh có tham gia câu lạc bộ nghệ thuật. Tính xác suất để học sinh đó là nam.

Một cuộc thi khoa học có 36 bộ câu hỏi, trong đó có 20 câu hỏi về chủ đề tự nhiên và 16 câu hỏi về chủ đề xã hội. Bạn An lấy ngẫu nhiên một bộ câu hỏi (lấy không hoàn lại), sau đỏ bạn Bình lấy ngẫu nhiên một câu hỏi. Xác suất bạn Bình lấy được bộ câu hỏi về chủ đề xã hội bằng

III. Vận dụng

Một chiếc hộp có 80 viên bi, trong đó 50 viên màu đỏ, 30 viên màu vàng ; các viên có kích thước và khối lượng như nhau. Sau khi kiểm tra, người ta thấy có 60% số viên bi màu đỏ đánh số và 50% viên bi màu vàng đánh số, những viên bi còn lại không đánh số. Khi đó:

a) Số viên bi màu đỏ có đánh số là 30.

b) Số viên bi màu vàng không đánh số là 15.

c) Lấy ra ngẫu nhiên một viên vi trong hộp. Xác suất để viên bi được lấy ra có đánh số là \(\frac{3}{5}.\)

d) Lấy ra ngẫu nhiên một viên bi trong hộp. Xác suất để viên bi được lấy ra không có đánh số là \(\frac{7}{{16}}.\)

Số mệnh đề đúng trong các mệnh đề trên là:

Một chiếc hộp có 80 chiếc bút bi, trong đó có 50 chiếc bút bi đỏ và 30 chiếc bút bi xanh; các bút bi có kích thước và khối lượng như nhau. Sau khi kiểm tra, ta thấy có 60% số bút bi đỏ có mực và 50% số bút bi xanh có mực, nhưng bút còn lại đều có mực. Lấy ra ngẫu nhiên một chiếc bút bi trong hộp. Xác suất để bút bi lấy ra đã hết mực là bao nhiêu?

Trong một trường học X, tỉ lệ học sinh nữ là 53%. Tỉ lệ học sinh nữ và tỉ lệ học sinh nam tham gia câu lạc bộ nghệ thuật lần lượt là 21% và 17%. Chọn ngẫu nhiên 1 học sinh của trường. Tính xác suất học sinh đó tham gia câu lạc bộ nghệ thuật.

Một trạm chỉ phát hai tín hiệu A và B với xác suất tương ứng là 0,85 và 0,15. Do có nhiễu trên đường truyền nên \(\frac{1}{7}\) tín hiệu A bị méo và thu được tín hiệu B còn \(\frac{1}{8}\) tín hiệu B bị méo và thu được tín hiệu A. Giả sử đã thu được tín hiệu A, tính xác suất thu được đúng tín hiệu lúc phát.

Một cửa hàng có ba loại trái cây: táo, chuối và cam với tỉ lệ là 50% lượng hoa quả trong cửa hàng là táo, 30% là chuối và 20% là cam. Xác suất bị hỏng khi để qua ngày mai của táo là 5%, chuối là 10% và cam là 2%. Lấy ngẫu nhiên một quả trong cửa hàng. Tính xác suất quả đó bị hỏng.

Trong một kì thi có 3 giám khảo chấm điểm là giám khảo A, B, C. Tỉ lệ thí sinh được đánh giá bởi từng giám khảo như sau: 40% thí sinh được đánh giá bởi giám khảo A, 35% thí sinh được đánh giá bởi giám khảo B và 25% thí sinh được đánh giá bởi giám khảo C. Xác suất thí sinh được giám khảo A cho điểm cao là 70%, giám khảo B là 80% và giám khảo C là 60%. Nếu một thí sinh được cho điểm cao, tính xác suất để đó là thí sinh được chấm bởi giám khảo A.