Cho cân tại A.Trên cạnh AB lấy điểm M, trên tia đối của tia CA lấy điểm N sao cho AM + AN = 2AB.
a) Chứng minh rằng: BM = CN
b) Chứng minh rằng: BC đi qua trung điểm của đoạn thẳng MN.
c) Đường trung trực của MN và tia phân giác của cắt nhau tại K. Chứng minh rằng từ đó suy ra KC vuông góc với AN
Giải bởi Vietjack
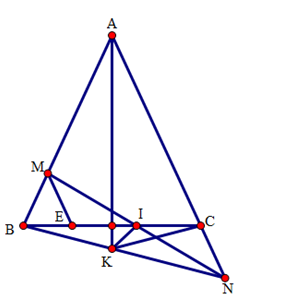
a) Do tam giác ABC cân tại A, suy ra AB = AC.
Ta có: AM + AN = AB – BM + AC + CN = 2AB – BM + CN.
Ta lại có AM + AN = 2AB (gt), nên suy ra
2AB – BM + CN = 2AB ⇔ – BM + CN = 0 ⇔ BM = CN.
Vậy BM = CN (đpcm).
b) Gọi I là giao điểm của MN và BC.
Qua M kẻ đường thẳng song song với AC cắt BC tại E.
Do ME // NC nên ta có:
(hai góc đồng vị) nên ∆BME cân tại M ⇒ BM = ME mà BM = CN nên ME = CN.
(hai góc so le trong)
(hai góc so le trong)
Ta chứng minh được
Suy ra MI = NI (hai cạnh tương ứng), từ đó suy ra I là trung điểm của MN.
c) Xét hai tam giác MIK và NIK có:
MI = IN (cmt),
IK là cạnh chung. Do đó
Suy ra KM = KN (hai cạnh tương ứng).
Xét hai tam giác ABK và ACK có: AB = AC(gt), (do BK là tia phân giác của ), AK là cạnh chung, do đó
Suy ra KB = KC (hai cạnh tương ứng).
Xét hai tam giác BKM và CKN có: MB = CN, BK = KN, MK = KC, do đó
suy ra . Mà (đpcm)Cho vuông cân tại A, tia phân giác của góc B và góc C cắt AC và AB lần lượt tại E và D.
a) Chứng minh BE = CD, AD = AE.
b) Gọi I là giao điểm của BE và CD, AI cắt BC tại M. Chứng minh vuông cân.
c) Từ A và D vẽ các đường thẳng vuông góc với BE. Các đường này cắt BC tại K và H. Chứng minh HK = KC.
Cho cân tại A, đường phân giác trong của góc B cắt AC tại D và cho biết AB = 15cm, BC = 10cm. Khi đó AD = ?
Cho tam giác ABC có AB = AC và tia phân giác góc A cắt BC ở H.
a) Chứng minh
b) Chứng minh AH ⊥ BC
c) Vẽ và . Chứng minh: DE // BC
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo AC và BD của hình bình hành ABCD.
a) Xác định giao tuyến của hai mặt phẳng (SBD) và (SAC).
b) Gọi K là trung điểm của SD. Tìm giao điểm G của BK với mặt phẳng (SAC); hãy cho biết tính chất của điểm G.
Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng (d) : y = (m - 3)x + 1 bằng
Cho có AB = 6cm, AC = 3cm, , M là điểm thỏa mãn . Tính độ dài đoạn AM.
Cho tứ giác ABCD có AC cắt BD tại O, . Gọi E là giao điểm của AD và BC CMR :
a) các tam giác AOB và DOC đồng dạng.
b) Các tam giác AOD và BOC đồng dạng.
c) EA . ED = EB . EC.
Cho ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.
Tính trung bình cộng hai đáy của một hình thang, biết rằng diện tích hình thang bằng 7m2 và chiều cao bằng 2m.
Hoa có 48 viên bi đỏ, 30 viên bi xanh và 60 viên bi vàng. Hoa muốn chia đều số bi vào các túi, sao cho mỗi túi có đủ 3 loại bi. Hỏi Hoa có thể chia vào nhiều nhất bao nhiêu túi mà mỗi túi có số bi mỗi màu bằng nhau.
Cho ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là các điểm đối xứng của H qua các cạnh AB, AC.
a) Chứng minh A, E, D thẳng hàng và BCED là hình thang.
b) Chứng minh .
c) Cho biết AB = 3cm, AC = 4cm. Tính DE và diện tích DHE.
Cho một số có hai chữ số, khi ta viết thêm vào bên trái số đó một chữ số 1 thì tổng của số mới và số đã cho là 168 . Tìm số đã cho.
Cho đường thẳng d và hai điểm A, B nằm cùng phía với d. Tìm điểm M trên d sao cho MA + MB đạt giá trị nhỏ nhất ?
