Cho nửa đường tròn (O) đường kính AB = 2R. Vẽ đường thẳng d là tiếp tuyến của (O) tại B. Trên cung AB lấy điểm M tùy ý tia AM cắt d tại N. Gọi C là trung điểm của AM tia CO cắt d tại D.
a ) CMR OBNC nội tiếp.
b ) CMR NO vuông góc với AD.
c ) CMR CA . CN = CO . CD
d ) Xác định vị trí điểm M để (2AM + AN ) đạt GTNN.
Giải bởi Vietjack
Câu a) Ta có: \[{\rm{\Delta OMA}}\] cân tại O và AC = MC nên \[OC \bot AM\;\] hay \[\widehat {OCN} = {90^0}\].
Xét tứ giác OBNC ta có :
\[\widehat {OCN} = {90^0}\] ( cmt )
\[\widehat {OBN} = {90^0}\] ( Tiếp tuyến vuông góc với bán kính )
\[ \Rightarrow \widehat {OCN} + \widehat {OBN} = {180^0}\]hay OBNC là tứ giác nội tiếp (đpcm )
Câu b ) Xét tam giác AND ta có :
AB là đường cao xuất phát từ đỉnh A.
DC là đường cao xuất phát từ đỉnh D.
Mà hai đường cao này cắt nhau tại O cho nên O là trực tâm của \[\Delta AND\]
NO cắt AD suy ra NO là đường cao của tam giác AND \[ \Rightarrow NO \bot AD\]
Câu c ) Ta có
\(\left\{ {\begin{array}{*{20}{c}}{\widehat {CAO} + \widehat {ANB} = {{90}^0}}\\{\widehat {CDN} + \widehat {ANB} = {{90}^0}}\end{array}} \right. \Rightarrow \widehat {CAO} = \widehat {CDN}\)
Xét tam giác CAO và tam giác CDN ta có :
\(\left\{ {\begin{array}{*{20}{c}}{\widehat {ACO} = \widehat {DCN}\left( { = {{90}^0}} \right)}\\{\widehat {CAO} = \widehat {CDB}\left( {cmt} \right)}\end{array}} \right.\)
\( \Rightarrow \Delta CAO \sim \Delta CDN\left( {g - g} \right)\)
\( \Rightarrow \frac{{CA}}{{CD}} = \frac{{CO}}{{CN}} \Rightarrow CA.CN = CO.CD\)( đpcm )
Câu d ) Xét tam giác AMB và tam giác ABN ta có :
\(\left\{ {\begin{array}{*{20}{c}}{\widehat {BAM}:\,chung}\\{\widehat {AMB} = \widehat {ABN}\left( { = {{90}^0}} \right)}\end{array}} \right.\)
\( \Rightarrow \Delta AMB \sim \Delta ABN\left( {g - g} \right)\)
\( \Rightarrow \frac{{AM}}{{AB}} = \frac{{AB}}{{AN}} \Rightarrow AM.AN = A{B^2} = 4{R^2}\)
Áp dụng BĐT cô – si ta có: \(2AM + AN \ge 2\sqrt {2AM.AN} = 2\sqrt {8{R^2}} = 4R\sqrt 2 \)
Vậy GTNN của 2AM + AN là \(4R\sqrt 2 \)khi và chỉ khi M là trung điểm của AN
Cho hbh ABCD. Gọi M và N là trung điểm của AB và CD. AN và CM cắt BD tại E và F.
Chứng minh \[\overrightarrow {DE} \, = \overrightarrow {EF} \;\, = \overrightarrow {FB} \]
Cho hình bình hành ABCD có AB = 2AD. Gọi E, F thứ tự là trung điểm của AB và CD
a) Các tứ giác AEFD, AECF là hình gì? Vì sao?
b) Gọi M là giao điểm của AF và DE, gọi N là giao điểm của BF và CE. Chứng minh rằng tứ giác EMFN là hình chữ nhật.
Hiện nay bố 32 tuổi, con 5 tuổi . Hỏi mấy năm nữa thì tuổi bố gấp 4 lần tuổi con?
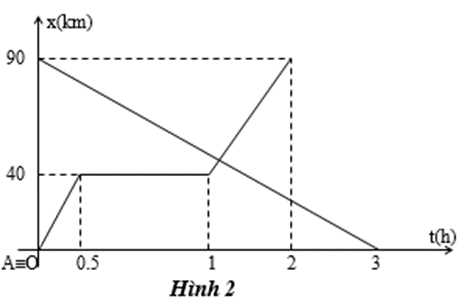
Cho đồ thị chuyển động của hai xe được mô tả trên hình vẽ.
a. Hãy nêu đặc điểm chuyển động của hai xe.
b. Tình thời điểm hai xe gặp nhau, lúc đó mỗi xe đi được quãng đường là bao nhiêu ?(Hình 2)
Biết chu vi của một hình chữ nhật gấp 6 lần chiều rộng. Hỏi chiều dài gấp mấy lần chiều rộng?
Hình thang có 2 cạnh bên bằng nhau có phải là hình thang cân không? Vì sao?
Một vật hình hộp chữ nhật có kích thước 30 . 20 . 10 (cm)
Ta thả ''nằm'' vật vào bình trụ đựng nước
a) Thể tích phần chòm của vật là bao nhiêu? Chiều cao phần vật chìm trong nước là mấy ?
b) Nếu ta đổ dầu vào cho vật ngập hoàn toàn thì thể tích vật ngập trong nước có thay đổi không ?
c) Lượng dầu đổ vào tối thiểu là mấy biết diện tích đáy bình trụ là 20dm2 . cho biết trọng lượng riêng nước, dầu, vật lần lượt là 10000N/m3; 8000N/m3; 9000N/m3 ?
Cho đường thẳng d \[y = \left( {2m + 1} \right).x - 2\]và m khác \(\frac{1}{2}\)giả sử d cắt ox tại a cắt oy tại b. Tìm m để diện tích tam giác OABbằng \(\frac{1}{2}\)
Tam giác ABC có hai đường trung tuyến BM, CN vuông góc với nhau và có BC = 3, góc \[\widehat {BAC} = {30^0}\]. Tính diện tích tam giác ABC.
Cho a, b N. Chứng tỏ rằng nếu 5a + 3b và 13a + 8b cùng chia hết cho 2012 thì a và b cũng chia hết cho 2012
Khi nhân một số với 39, một học sinh đã đặt nhầm các tích riêng thẳng cột nên tìm ra kết quả là 259,2. Tìm tích đúng.
