Lời giải
Chọn A
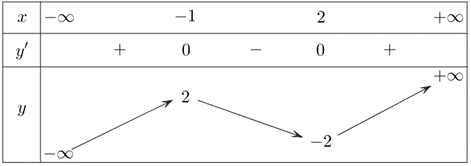
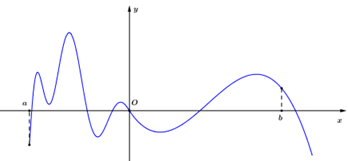
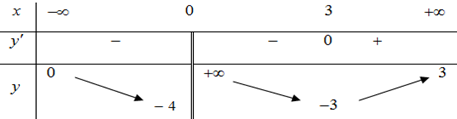
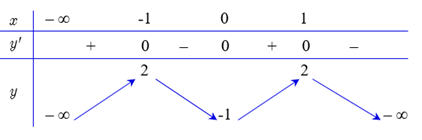
Từ bảng biến thiên của \(f\left( x \right)\) ta suy ra bảng biến thiên của \(\left| {f\left( x \right)} \right|\) như sau
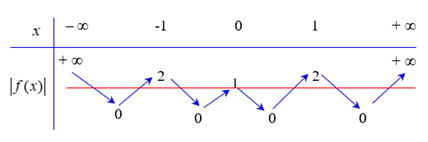
Đặt \(t = \cos 2x \in \left[ { - 1;1} \right]\).
Dựa vào bảng biến thiên trên, phương trình \(\left| {f\left( t \right)} \right| = 1\) chỉ có 3 nghiệm thuộc \(\left( { - 1;1} \right)\).
Ta có \(\left| {f\left( t \right)} \right| = 1 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = a \in \left( { - 1;0} \right)}\\{t = 0}\\{t = b \in \left( {0;1} \right)}\end{array}} \right.\).
Do \(x \in \left[ {0;\frac{{3\pi }}{2}} \right] \Leftrightarrow 2x \in \left[ {0;3\pi } \right]\).
Xét đường tròn lượng giác
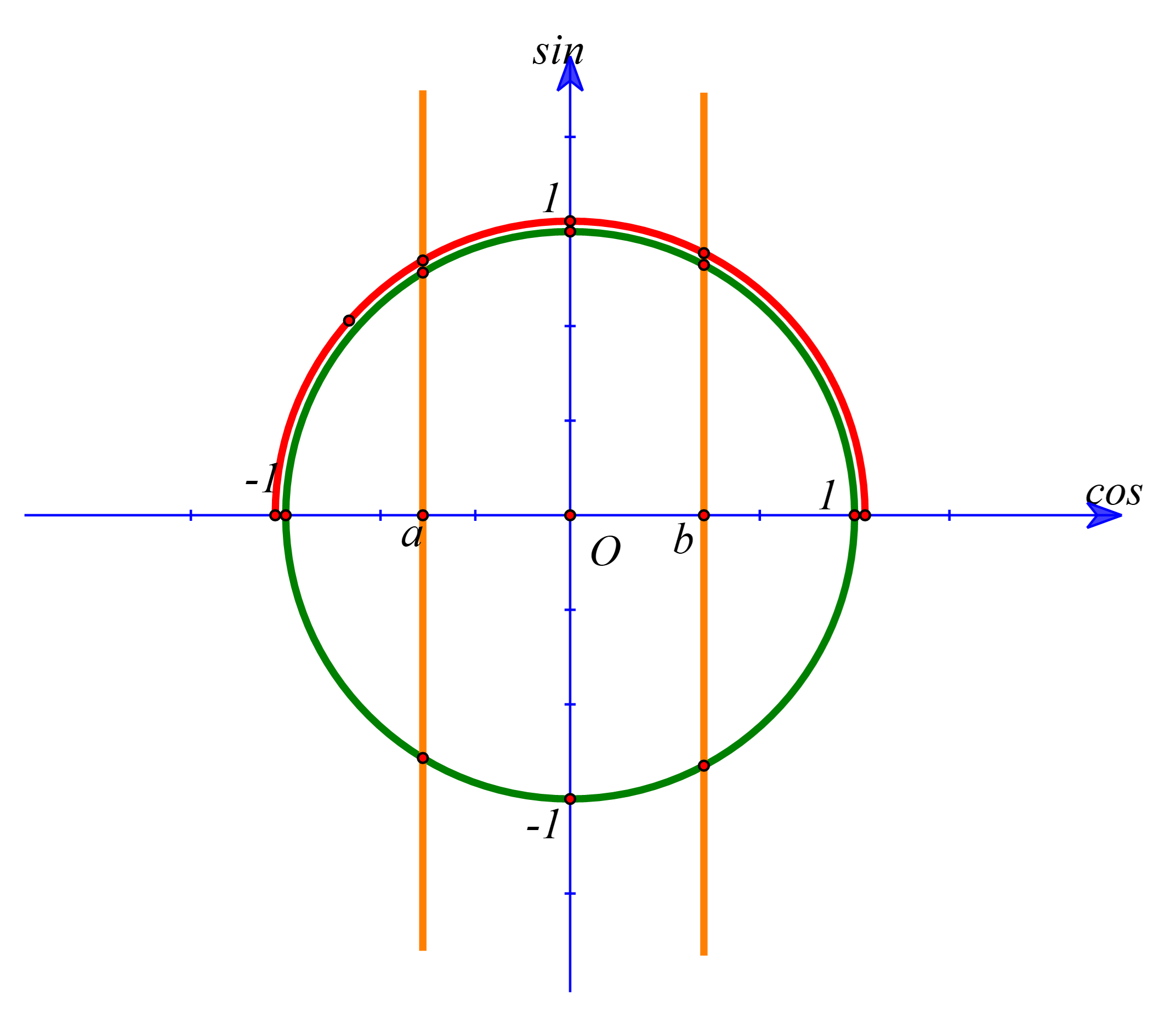
Phương trình \(\cos 2x = a,a \in \left( { - 1;0} \right)\) có 3 nghiệm phân biệt thuộc \(\left[ {0;\frac{{3\pi }}{2}} \right]\).
Phương trình \(\cos 2x = b,a \in \left( {0;1} \right)\) có 3 nghiệm phân biệt thuộc \(\left[ {0;\frac{{3\pi }}{2}} \right]\).
Phương trình \(\cos 2x = 0\) có 3 nghiệm phân biệt thuộc \(\left[ {0;\frac{{3\pi }}{2}} \right]\).
Vậy số nghiệm thuộc \(\left[ {0;\frac{{3\pi }}{2}} \right]\) của phương trình \(\left| {f\left( {\cos 2x} \right)} \right| = 1\) là 9 nghiệm.
Phân tích phương án nhiễu:
B: Học sinh nhầm \(\left| {f\left( {\cos 2x} \right)} \right| = 1\) chỉ có 4 nghiệm phân biệt dựa vào BBT.
C: Học sinh nhầm \(\left| {f\left( {\cos 2x} \right)} \right| = 1\) có 7 nghiệm phân biệt dựa vào BBT sau khi lấy đối xứng.
D: Học sinh nhầm \(\left| {f\left( {\cos 2x} \right)} \right| = 1\) có 10 nghiệm phân biệt do nhầm lẫn \(\sin 2x\) và \(\cos 2x\).
 Giải bởi Vietjack
Giải bởi Vietjack