Giải bởi Vietjack
Lời giải
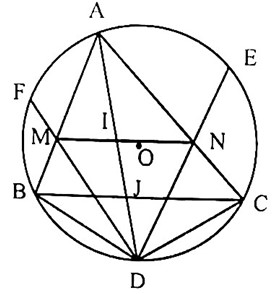
Gọi (Q) là đường thẳng Ơ-le, H là trực tâm, K là trung điểm AH, M là giao AH và BC.
Suy ra M, K, D ∈ (Q)
Gọi P là đầu thứ hai đường kính qua A.
Suy ra CP // BH (cùng ⊥ AC), BP // CH (cùng ⊥ AB)
Nên BPCH là hình bình hành
Do đó HP cắt BC tại trung điểm BC, tức HP đi qua D ⇒ OD là đường trung bình của ∆PAH ⇒ OD = \[\frac{{AH}}{2}\] = AK
⇒ AODK là hình bình hành ⇒ DK // AO ⇒ DD' trùng với DK
Do đó DK là đường kính của (Q), tức DD' đi qua tâm đường thẳng Euler
Vậy nên EE', FF' cũng đi qua tâm đường thẳng Euler.
Cho tam giác nhọn ABC có đường cao AH. Từ H kẻ HF vuông góc với AB (F ∈ AB) và kẻ HE ⊥ vói AC (E ∈ AC).
a) Chứng minh: \[\widehat {AFE} = \widehat {ACB}\].
b) Hai đường thẳng EF và BC cắt nhau tại M. Chứng minh ME . MF = MB . MC.
Cho đường tròn tâm O, đường kính AB và điểm C thuộc đường tròn sao cho AC > BC. Qua O vẽ đường thẳng vuông góc với dây AC ở H. Kẻ tiếp tuyến tại A của đường tròn cắt tia OH ở D. BD cắt đường tròn tâm O ở E.
a) Chứng minh HA = HC.
b) Biết \[\widehat {DCO} = 90^\circ \]. Chứng minh OH . DO = DE . DB.
c) Trên tia đối của EA lấy F sao cho E là trung điểm AF. Từ F vẽ đường thẳng AD vuông góc ở K; KF cắt BC ở M. Chứng minh MK = MF.
Cho hình bình hành ABCD có BC = 2AB và \[\widehat A = 60^\circ \]. Gọi E, F theo thứ tự là trung điểm của BC và AD.
a) Tứ giác ECDF là hình gì? Vì sao?
b) Tam giác DEC là tam giác gì? Vì sao?
c) Tính số đo\[\widehat {AED}\]?
Cho ba điểm A(– 4; 0), B(0; 3) C(2; 1).
a) Xác định tọa độ \[\overrightarrow u = 2\overrightarrow {AC} \;--\overrightarrow {AB} \].
b) Tìm điểm M sao cho MA + 2MB + 3MC = 0.
Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo (không vuông góc), I và K lần lượt là trung điểm của BC và CD. Gọi M và N theo thứ tự là điểm đối xứng của điểm O qua tâm I và K.
a) Chứng minh rằng tứ giác BMND là hình bình hành.
b) Với điều kiện nào của hai đường chéo AC và BD thì tứ giác BMND là hình chữ nhật?
c) Chứng minh ba điểm M, C, N thẳng hàng.
Cho tam giác ABC cân tại A, đường phân giác trong của góc B cắt AC tại D và cho biết AB = 15cm, BC = 10cm. Khi đó AD = ?
Trong mặt phẳng tọa độ Oxy cho parabol (P): y = \[ - \frac{1}{2}\]x2 và đường thẳng (d) y = mx + m – 3(với m là tham số).
a) Khi m = –1, tìm tọa độ giao điểm của đường thẳng (d) và parabol (P).
b) Tìm m để đường thẳng (d) và parabol (P)cắt nhau tại 2 điểm phân biệt có hoành độ x1, x2 thỏa mãn hệ thức x12 + x22 = 14.
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
a) Chứng minh rằng: OA ⊥ BC.
b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.
c) Tính độ dài các cạnh của ∆ ABC; Biết OB = 2 cm, OA = 4 cm.
Cho hai đường tròn (O; R) và (O'; R') tiếp xúc ngoài tại A (R > R'). Vẽ dây AM của đường tròn (O) và dây AN của đường tròn (O') sao cho AM ⊥ AN. Gọi BC là tiếp tuyến chung ngoài của hai đường tròn (O) và (O') với B thuộc (O) và C thuộc (O').
a) Chứng minh ba đường thẳng MN, BC và OO' đồng quy.
b) Xác định vị trí của M và N để tứ giác MNOO' có diện tích lớn nhất. Tính giá trị lớn nhất đó.
Cho ∆ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với H qua AB, gọi E là điểm đối xứng với H qua AC.
a) Chứng minh rằng D đối xứng với E qua A.
b) Tam giác DHE là tam giác gì? Vì sao?
c) Tứ giác BDEC là hình gì? Vì sao?
d) Chứng minh rằng BC = BD + CE.
a) Chứng minh: AMNB là hình thang cân;
b) Chứng minh: MNPD là hình bình hành;
c) Chứng minh: DM vuông góc AN.
