Cho đường tròn tâm O và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Đường thẳng d thay đổi đi qua M cắt đường tròn tại 2 điểm phân biệt C và D (C nằm giữa M và D)
a) Chứng minh tứ giác AMBO nội tiếp
b) Chứng minh MA2 = MC.MD
c) Chứng minh đường tròn ngoại tiếp tam giác OCD luôn đi qua điểm cố định khác O
Giải bởi Vietjack
Lời giải
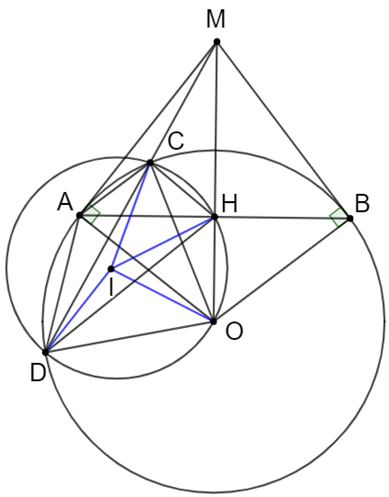
a) Xét tứ giác AOBM với \(\widehat {MAO}\) và \(\widehat {MBO}\) có:
\(\widehat {MAO} + \widehat {MBO} = 90^\circ + 90^\circ = 180^\circ \).
Do đó AOBM là tứ giác nội tiếp đường tròn.
b) Xét ∆MCA và ∆MAD có:
\(\widehat {MAC} = \widehat {MDA}\) (góc tạo bởi tia tiếp tuyến và dây cung, góc nội tiếp đường tròn cùng chắn cung AC)
\(\widehat M\) là góc chung
Þ ∆MCA ᔕ ∆MAD (g.g)
\( \Rightarrow \frac{{MC}}{{MA}} = \frac{{MA}}{{MD}} \Rightarrow M{A^2} = MC.MD\)
c) Lấy H là giao điểm của MO và AB.
Vì I là tâm đường tròn ngoại tiếp tam giác COD
Áp dụng hệ thức lượng trong tam giác vuông MAO vuông tại A có AH là đường cao nên suy ra MA2 = MH.MO.
Mà MA2 = MC.MD (cmt)
Þ MH.MO = MC.MD
\(\frac{{MH}}{{MD}} = \frac{{MC}}{{MO}}\)
Xét ∆MHD và ∆MCO có:
\(\frac{{MH}}{{MD}} = \frac{{MC}}{{MO}}\) (cmt)
\(\widehat M\): góc chung
Þ ∆MHD ᔕ ∆MCO (g.g)
\( \Rightarrow \widehat {MDH} = \widehat {MOC} \Rightarrow \widehat {CDH} = \widehat {HOC}\)
Þ Tứ giác CHOD nội tiếp đường tròn (Hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại với hai góc bằng nhau).
Þ H thuộc đường tròn (I).
Vậy (I) đi qua điểm cố định H là giao của MO và AB; với A, B là hai tiếp điểm từ điểm M cố định đến đường tròn (O).
Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB tới đường tròn (O) với A, B là các tiếp điểm.
a) Chứng minh bốn điểm A, B, M, O cùng thuộc một đường tròn.
b) Kẻ đường kính AC của đường tròn (O). Chứng minh OM // CB.
c) Vẽ BK vuông góc với AC tại K. Chứng minh: CK.OM = OB.CB.
d) Tiếp tuyến tại C của đường tròn (O) cắt AB tại D. Chứng minh OD ^ CM.
Cho đường tròn (O; R) có đường kính AB. Vẽ các tiếp tuyến Ax, By của đường tròn (O), trên đường tròn (O) lấy một điểm E bất kì (E khác A, B). Tiếp tuyến tại E của đường tròn (O) cắt Ax, By lần lượt tại C, D.
a) CM: CD = AC + BD.
b) Vẽ EF vuông góc AB tại F, BE cắt AC tại K. CM: AF.BC = KE.EB.
c) EF cắt CB tại I. CM tam giác AFC đồng dạng với tam giác BFD, suy ra FE là tia phân giác của góc CFD.
d) EA cắt CF tại M. EB cắt DF tại N. CM: M, I, N thẳng hàng.
Cho phương tình 3x − 2y = 6. (1)
a) Viết công thức nghiệm tổng quát của phương trình (1);
b) Tìm nghiệm nguyên của phương trình (1).
Cho đường tròn tâm O và BC là dây cung không đi qua tâm. Trên tia đối của tia BC lấy điểm M sao cho M không trùng với B. Đường thẳng đi qua M cắt đường tròn (O) đã cho tại N và P (N nằm giữa M và P) sao cho O nằm trong PMC. Gọi A là điểm chính giữa của cung nhỏ NP. Các dây AB và AC lần lượt cắt NP tại D và E.
a) Chứng minh tứ giác BDEC nội tiếp.
b) Chứng minh MB.MC = MN.MP.
Cho tứ giác ABCD có \(\widehat B = \widehat D = 90^\circ \).
a) CMR: 4 điểm A, B, C, D cùng thuộc một đường tròn, tìm tâm đường tròn đó.
b) So sánh độ dài AC và BD. Tứ giác ABCD cần thêm điều kiện gì thì AC = BD
Cho nửa đường tròn (O), đường kính AB; Ax là tiếp tuyến của nửa đường tròn. Trên nửa đường tròn lấy điểm D (D khác A, B). Tiếp tuyến tại D của (O) cắt Ax ở S.
a) Chứng minh SO // BD.
b) BD cắt AS ở C. Chứng minh SA = SC.
c) Kẻ DH vuông góc với AB; DH cắt BS tại E. Chứng minh E là trung điểm của DH.
Cho đường tròn (O), đường kính AB, vẽ các tiếp tuyến Ax, By. Từ M trên đường tròn (M khác A,B) vẽ tiếp tuyến thứ ba nó cắt Ax ở C cắt By ở D. Gọi N là giao điểm của BC và AD.
a) CMR: \(\frac{{CN}}{{AC}} = \frac{{NB}}{{BD}}\).
b) CM: MN ^ AB.
c) CMR: \(\widehat {COD} = 90^\circ \).
