Cho tam giác ABC vuông tại A có AC = 2AB. Vẽ tia phân giác Ax của A. Từ B vẽ đường thẳng vuông góc với Ax cắt AC tại F. Từ C vẽ đường thẳng vuông góc Ax cắt Ax tại E.
a) CMR: Tứ giác ABEF có bốn cạnh bằng nhau.
b) CMR: Tứ giác BECF là hình bình hành.
c) Vẽ trung tuyến AM và đường cao AH. BF cắt AH và AM tại P và Q. Hỏi APEQ là hình gì?
Giải bởi Vietjack
Lời giải
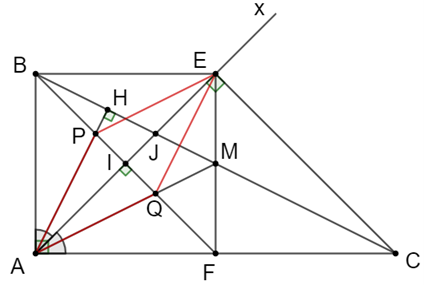
Lấy I là giao của Ax và BF.
a) AI là tia phân giác của góc BAF và AI cũng là đường cao của tam giác BAF nên
∆BAF cân tại A nên AB = AF.
Mà \(\widehat {BAF} = 90^\circ \).
Khi đó ABEF là hình vuông.
Vậy ABEF có bốn cạnh bằng nhau.
b) Ta có: BE = AF = BA.
Mà AC = 2BA nên AC = 2AF Þ FC = AF = BE.
Lại có BE // AF Þ BE // FC.
Vậy BECF là hình bình hành.
c) Vì tứ giác ABEF là hình vuông nên I là trung điểm AE.
Xét tam giác ABC vuông tại A có AM là trung tuyến
Suy ra AM = MB = MC (tính chất trung tuyến tam giác vuông)
Þ Tam giác AMC cân tại M
\( \Rightarrow \widehat {MAC} = \widehat {MCA}\)
Mà \(\widehat {MCA} = \widehat {BAH}\) (cùng phụ \(\widehat {ABC}\))
\( \Rightarrow \widehat {MAC} = \widehat {BAH}\)
• Xét ∆ABP và ∆AFQ có:
AB = AF
\(\widehat {BAP} = \widehat {FAQ}\)
\(\widehat {ABP} = \widehat {AFQ}\) (do ∆ABF cân tại A)
Do đó ∆ABP = ∆AFQ (g.c.g)
Suy ra AP = AQ (hai cạnh tương ứng).
Suy ra ∆APQ cân tại A, có AI là đường cao nên AI đồng thời là trung tuyến.
Do đó I là trung điểm PQ.
• Xét tứ giác APEQ có: I là trung điểm AE và PQ.
Suy ra tứ giác APEQ là hình bình hành.
Lại có AE vuông góc PQ.
Vậy tứ giác APEQ là hình thoi.
Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm.
a) Tính số đo góc B, góc C (làm tròn đến độ) và đường cao AH.
b) Chứng minh rằng: \(AB.\cos B + AC.\cos C = BC.\)
c) Trên cạnh AC lấy điểm D sao cho DC = 2DA. Vẽ DE vuông góc với BC tại E. Chứng minh rằng: \(\frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{4}{{9D{E^2}}}\)
Cho nửa đường tròn tâm O đường kính AB và M là điểm nằm trên (O). Tiếp tuyến tại M cắt tiếp tuyến tại A và B của (O) lần lượt ở C và D. Đường thẳng AM cắt OC tại E, đường thẳng BM cắt OD tại F.
a) Chứng minh: \(\widehat {COD} = 90^\circ \).
b) Tứ giác MEOF là hình gì?
c) Chứng minh AB là tiếp tuyến của đường tròn đường kính CD.
Cho tam giác ABC vuông tại A, đường cao AH.
a) Biết AB = 4 cm, \(AC = 4\sqrt 3 \;cm\). Giải tam giác ABC.
b) Kẻ HD, HE lần lượt vuông góc với AB, AC (D ∈ AB, E ∈ AC). Chứng
minh BD.DA + CE.EA = AH2.
c) Lấy diểm M nằm giữa E và C, kẻ AI vuông góc với MB tại I. Chứng minh:
\[\sin \widehat {AMB}\,\,.\,\sin \widehat {ACB} = \frac{{HI}}{{CM}}\].
Cho tam giác ABC vuông tại A, đường cao AH.
a) Biết AB = 4 cm, \(AC = 4\sqrt 3 \;cm\). Giải tam giác ABC.
b) Kẻ HD, HE lần lượt vuông góc với AB, AC (D thuộc AB, E thuộc AC). Chứng
minh BD.DA + CE.EA = AH2.
c) Lấy diểm M nằm giữa E và C, kẻ AI vuông góc với MB tại I. Chứng minh:
\[\sin \widehat {AMB}\,.\,\sin \widehat {ACB} = \frac{{HI}}{{CM}}\].
Cho hình chữ nhật ABCD có (AD < AB). Qua C kẻ đường thẳng vuông góc với đường chéo AC tại C, cắt đường thẳng AD, AB lần lượt tại M, N.
a) Chứng minh rằng AB.AN = AD.AM.
b) Cho AD = 3 cm, AB = 4 cm. Tính DM và SAMN.
c) Chứng minh CD.CB = AB.AD.
d) Gọi E là trung điểm của MC, kẻ CH vuông DB tại H. Cho EB cắt CH tại K. Chứng minh K là trung điểm của CH.
Cho đường tròn tâm O đường kính BC, điểm A thuộc đường tròn. Vẽ bán kính OK song song với BA (K và A nằm cùng phía đối với BC) tiếp tuyến đường trong tâm O tại C cắt ở I , OI cắt tại H.
a) Chứng minh tam giác ABC là tam giác vuông tại A.
b) Chứng minh IA là tiếp tuyến của đường tròn tâm O.
c) Cho BC = 30 cm; AB = 18 cm, tính các độ dài OI và CI.
Chứng minh rằng trong tam giác ABC ta có các hệ thức:
a) sin A = sin B.cos C + sin C.cos B;
b) ha = 2R.sin B.sin C.
Cho hình chữ nhật ABCD có AB > BC. Qua B kẻ đường thẳng vuông góc với AC, đường thẳng này cắt AC tại H, cắt CD tại M.
a) Chứng minh ΔCMH ᔕ ΔCAD.
b) Chứng minh BC2 = CM.CD. Tính độ dài đoạn MC, biết AB = 8 cm, BC = 6 cm.
c) Kẻ MK vuông góc với AB tại K, MK cắt AC tại điểm I. Chứng minh \(\widehat {BIM} = \widehat {AMC}.\)
Cho tam giác ABC có các đường phân giác cắt nhau tại N cho ha, hb, hc là đường cao gọi r là khoảng cách từ N đến cạnh tam giác. Chứng minh rằng:
\[\frac{1}{{{h_a}}} + \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}} = \frac{1}{r}\]
