Cho hình chop đều SABC có cạnh bên bằng a hợp với đáy ABC một góc 60°. Tính thể tích hình chop SABC theo a.
Giải bởi Vietjack
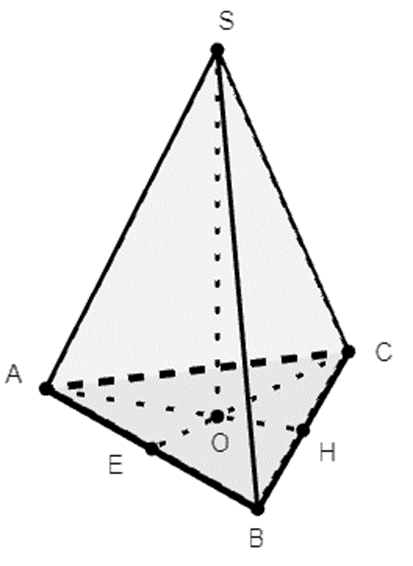
Gọi O là tâm của tam giác ABC
Suy ra \(SO \bot SABC\) (do SABC đều)
Khi đó góc hợp giữa SC và (ABC) là góc: \(\widehat {SCO} = 60^\circ \)
Xét ∆SOC vuông tại A.
\(SO = \sin 60^\circ .SC = \frac{{\sqrt 3 }}{2}a\)
\(OC = \cos 60^\circ .SC = \frac{1}{2}a\)
\( \Rightarrow CE = \frac{3}{2}OC = \frac{3}{4}a\) (tính chất của đường trung tuyến tam giác đều)
\( \Rightarrow AB = \frac{2}{{\sqrt 3 }}.CE = \frac{{2\sqrt 3 }}{4}a = \frac{{\sqrt 3 }}{2}a\)
\( \Rightarrow {V_{SABC}} = \frac{1}{3}.SO.{S_{ABC}} = \frac{1}{3}.\frac{{\sqrt 3 }}{2}a.\frac{1}{2}.\frac{3}{4}a.\frac{{\sqrt 3 }}{2}a = \frac{{3{a^3}}}{{32}}\).
Phân tích đa thức thành nhân tử: 12x2 + 5x – 12y2 + 12y – 10xy – 3
Năm nay Lan được 12 tuổi còn mẹ của Lan thì được 32 tuổi. Hỏi sau 8 năm nữa thì số tuổi của mẹ gấp mấy lần số tuổi của Lan?
Cho định lí "Cho số tự nhiên n, nếu n5 chia hết cho 5 thì n chia hết cho 5". Định lí này được viết dưới dạng P ⇒ Q.
Phát biểu định lí trên bằng các dùng thuật ngữ "điều kiện đủ".
Mẹ có một số kẹo. Nếu mẹ chia số kẹo thành 6 phần bằng nhau thì dư 3 cái.
a) Hỏi với số kẹo đó, mẹ có thể chia thành 3 phần bằng nhau hay không? Vì sao?
b) Với số kẹo đó, mẹ có thể chia thành 2 phần bằng nhau không? Vì sao?
Cô giáo cho một số kẹo. Nếu cô chia số kẹo đó thành 12 phần như nhau thì dư 6 chiếc. Hỏi cô có thể chia đều số kẹo thành 4 phần mà không còn dư hay không?
Cho trước hai điểm phân biệt A, B. Tìm tập hợp các điểm M thỏa mãn:
\(\left| {\overrightarrow {MA} } \right| = \left| {\overrightarrow {MB} } \right|\).
Giá trị nghiệm nguyên của phương trình:
12x2 + 6xy + 3y2 = 28(x + y).
Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM // OQ.
(M ∈ OP), IN // OP (N ∈ OQ). Chứng minh rằng:
1) Tam giác IMN cân tại I.
2) OI là đường trung trực của MN.
Cho tam giác ABC vuông tại A có \(\widehat B = 60^\circ \).
a) Tính số đo góc C.
b) Trên BC lấy E sao cho BE = BA, tia phân giác của góc B cắt AC tại D. Chứng minh: DE = AD.
Cho hai điểm B; C phân biệt. Tập hợp những điểm M thỏa mãn \(\overrightarrow {CM} .\overrightarrow {CB} = {\overrightarrow {CM} ^2}\) là:
Cho tứ giác ABCD có hai góc đối ở đỉnh B và D cùng bằng 90°. Gọi O là trung điểm của AC. Chứng minh bốn điểm A, B, C, D cùng thuộc đường tròn đường kính AC.
Tìm nghiệm của phương trình sau trong khoảng đã cho:
\(\sin 2x = \frac{{ - 1}}{2}\), x ∈ (0; π).
