Cho hình chóp S.ABCD có AD không song song với BC, lấy I ∈ SA so cho SA = 3IA, lấy J ∈ SC; M là trung điểm SB.
a. Tìm giao tuyến của (SAD) và (SBC).
b. Tìm giao điểm E của AB và (IJM).
c. Tìm giao điểm F của BC và (IJM).
d. Tìm giao điểm N của SD và (IJM).
e. Gọi H = MN ∩ BD. Chứng minh rằng: H, E, F thẳng hàng.
 Giải bởi Vietjack
Giải bởi Vietjack
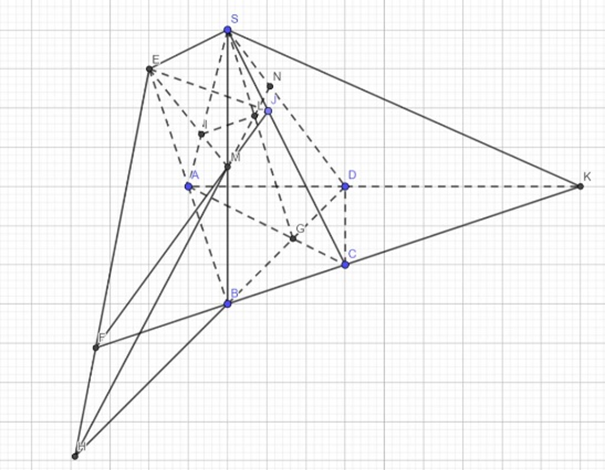
a. Gọi \(AD \cap BC = K \Rightarrow \left( {SAD} \right) \cap \left( {SBC} \right) = SK\)
b. Gọi \(IM \cap AB = E \Rightarrow AB \cap \left( {IJM} \right) = E\)
c. Gọi \(JM \cap BC = F \Rightarrow BC \cap \left( {IJM} \right) = F\)
d. Gọi \(AC \cap BD = G,AG \cap IJ = L,ML \cap SD = N \Rightarrow N = SD \cap \left( {IJM} \right)\)
e. Ta có: \(MN \cap BD = H \Rightarrow H \in \left( {MIJ} \right),H \in \left( {ABCD} \right) \Rightarrow H \in \left( {MNJ} \right) \cap \left( {ABCD} \right)\)(Hay H thuộc giao tuyến của \(\left( {MNJ} \right);\left( {ABCD} \right)\)
Lại có \(E \in \left( {MIJ} \right) \Rightarrow E \in \left( {MNJ} \right),E \in AB \Rightarrow E \in \left( {ABCD} \right)\)
\(F \in MJ \Rightarrow F \in \left( {MNJ} \right) \cap \left( {ABCD} \right)\)⇒ H, E, F thẳng hàng (cùng thuộc giao tuyến của (MNJ) và (ABCD).
Cho đường tròn (O; R) và dây AB = 1,6R. Vẽ 1 tiếp tuyến song song AB cắt các tia OA, OB theo thứ tự tại M và N. Tính \({S_{_{\Delta OMN}}}\) theo R.
Cho đường tròn (O) đường kính BC và 1 điểm A nằm trên đường tròn (A ≠ B và C). Qua O, kẻ tia Ox // AC, tia Ox cắt AB tại D.
a. Chứng minh: OD ⊥ AB và từ đó suy ra D là trung điểm của AB.
b. Tiếp tuyến tại B của (O) cắt tia Ox tại E. Chứng minh: EA cũng là tiếp tuyến của (O).
c. Tia CA cắt tia BE tại F. Chứng minh: Tia CE đi qua trung điểm I của đường cao AH.
Cho hình bình hành ABCD có AD = 2AB. Từ C kẻ CE ⊥ AB, nối E với trung điểm M của AD, từ M kẻ MF ⊥ CE, MF ∩ BC = N.
a. Hỏi MNCD là hình gì?
b. ∆EMC là tam giác gì?
c. Chứng minh \(\widehat {BAD} = 2\widehat {AEM}\)
Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho AM = BN = CP = DQ < AB. Chứng minh tứ giác MNPQ là hình vuông.
Cho hình chữ nhật ABCD, vẽ ∆AEC vuông tại E. Chứng minh năm điểm A, B, C, D, E cùng thuộc một đường tròn.
Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và đáy bằng 30°. Thể tích khối chóp S.ABC bằng ?
Cho đường tròn tâm O, đường kính AB = 10 cm. Trên đường tròn tâm O lấy điểm C sao cho AC = 6 cm . Kẻ CH ⊥ AB tại H.
a. So sánh dây AB và dây BC.
b. ∆ABC là tam giác gì? Vì sao?
c. Từ O kẻ OI ⊥ BC tại I. Tính độ dài OI.
d. Tiếp tuyến tại A của đường tròn (O) cắt tia BC tại E.
Chứng minh CE × CB = AH × AB.
Cho hình bình hành ABCD và điểm M tùy ý.
Chứng minh rằng \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \).
Cho ∆ABC. Chứng minh rằng: \(\cot A + \cot B + \cot C = \frac{{{a^2} + {b^2} + {c^2}}}{{4S}}\).
Trong mặt phẳng tọa độ (Oxy), cho phép biến hình F có biểu thức tọa độ \(x' = \frac{{ - 3x + 4y}}{5};y' = \frac{{4x + 3y}}{5}\). Ảnh của \(\Delta :x + y = 0\) qua phép biến hình F là ?
Cho ∆ABC. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Cho diện tích ∆ABC bằng 24 cm2. Tính diện tích ∆MNP.
Cho hình bình hành ABCD và điểm E bất kì.
Chứng minh \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = \overrightarrow {AE} \).
Tìm m để phương trình 3cot2x – 2m = 0 có nghiệm trong khoảng \(\left( {0;\frac{\pi }{4}} \right)\).