Hai sọt cam nặng tổng cộng 76,65kg. Nếu lấy 4kg ở sọt thứ nhất chuyển sang sọt thứ hai thì sọt thứ hai nặng hơn sọt thứ nhất 1,85kg. Hỏi mỗi sọt cam nặng bao nhiêu ki–lô–gam ?
Giải bởi Vietjack
Sau khi chuyển sọt thứ nhất là:
(76,65 – 1,85) : 2 = 37,4 (kg)
Lúc đầu sọt thứ nhất nặng là :
37,4 +4 = 41,4 (kg)
Lúc đầu sọt thứ hai nặng là :
76,65 – 41,4 = 35,25 (kg)
Cho đường tròn (O; R) có đường kính AB, lấy điểm M thuộc đường tròn (O) sao cho AM < MB. Tiếp tuyến tại A của đường tròn (O) cắt tia OM tại S. Đường cao AH của tam giác SAO (H thuộc SO) cắt đường tròn (O) tại D.
1. Chứng minh SD là tiếp tuyến của đường tròn (O).
2. Kẻ đường kính DE của đường tròn (O). Gọi r là bán kính đường tròn nội tiếp tam giác SAD. Chứng minh M là tâm đường tròn nội tiếp tam giác SAD và tính độ dài đoạn thẳng AE theo R và r.
3. Cho AM = r. Gọi K là giao điểm của BM và AD. Chứng minh: \(\frac{{M{D^2}}}{6} = KH.KD\).
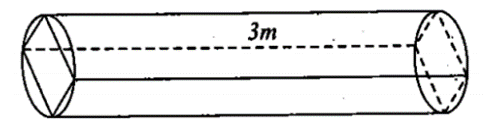
Một khúc gỗ hình trụ có chiều cao 3m, đường kính đáy 80 cm. Người ta cưa 4 tấm bìa để được một khối lăng trụ đều nội tiếp trong khối trụ. Tổng thể tích của 4 tắm bìa bị cưa là (xem mạch cửa không đáng kể).
Cho đường tròn (O ; R) và một điểm A sao cho OA = 2R vẽ các tiếp tuyến AB, AC với (O; R) , B và C là các tiếp điểm. Vẽ đường kính BOD.
a) Chứng minh 4 điểm A, B, O, C cùng thuộc một đường tròn.
b) Chứng minh DC song song với OA.
c) Đường trung trực của BD cắt AC và CD lần lượt tại S và E. Chứng minh OCEA là hình thang cân.
Tìm hai số biết tổng của hai số đó là 56,9; nếu thêm vào số bé 6,25 đơn vị và bớt ở số lớn đi 6,25 đơn vị thì được hai số bằng nhau.
Mua 0,5 kg nho và 1 kg táo phải trả 60 000 đồng. Mua 1 kg nho và 0,5 kg táo phải trả 72 000 đồng. Tính giá tiền mua 1 kg nho và giá tiền mua 1 kg táo.
Cho tam giác ABC đều cạnh 2a, d là đường thẳng qua A và song song BC. Khi M di động trên d thì giá trị nhỏ nhất của \(\left| {\overrightarrow {MA} + 2\overrightarrow {MB} - \overrightarrow {MC} } \right|\) là?
Tổng của hai số lẻ bằng 64. Tìm 2 số đó,biết rằng giữa chúng có 5 số chẵn liên tiếp.
Một thùng mì chính có 60 gói , mỗi gói nặng 453g. Hỏi 25 thùng mì chính như thế nặng bao nhiêu kg ?
Cứ 4 vỏ chai nước ngọt thì có thể đổi được 1 chai nước ngọt. Nếu bạn có 32 vỏ chai nước ngọt thì bạn có thể đổi được bao nhiêu chai nước ngọt?
Cho biểu thức P = \(\left( {\frac{{{x^2}}}{{{x^3} - 4x}} + \frac{6}{{6 - 3x}} + \frac{1}{{x + 2}}} \right):\left( {x - 2 + \frac{{10 - {x^2}}}{{x + 2}}} \right)\).
a) Rút gọn P.
b) Tính giá trị của biểu thức P khi \(\left| x \right| = \frac{3}{4}\).
c) Với giá trị nào của x thì P = 7.
d) Tìm giá trị nguyên của x để P có giá trị nguyên.
Cho đường tròn (O; R) có đường kính BC. Lấy A thuộc (O) sao cho AB < AC, vẽ đường cao AH của tam giác ABC.
a) Chứng minh: AH.BC = AB.AC.
b) Tiếp tuyến tại A của (O) cắt đường thẳng BC tại M. Chứng minh rằng: MA2 = MB.MC.
c) Kẻ HE vuông góc với AB (E thuộc AB) và HF vuông góc với AC (F thuộc AC). Chứng minh AM song song với EF.
Hai kho thóc chứa tất cả 1,45 tấn thóc ,biết nếu chuyển 0,12 tấn thóc từ kho A sang kho B thì lúc này số thóc ở kho A bằng \(\frac{2}{3}\)số thóc ở kho B. Hỏi lúc đầu mỗi kho chứa tất cả bao nhiêu tấn thóc ?
Một khu vườn hình chữ nhật có chiều dài hơn chiều rộng 15m. Nếu người ta bớt chiều dài đi \(\frac{2}{3}\) và bớt chiều rộng đi \(\frac{5}{9}\) thì khu vườn trở thành hình vuông. Tính diện tích khu vườn.
Cho hình vuông ABCD, O là giao điểm hai đường chéo AC và BD. Gọi M và N lần lượt là trung điểm của OB và CD.
a) CMR: \(\widehat {AMN} = 90^\circ \). Từ đó suy ra bốn điểm A, M, N, D cùng thuộc một đường tròn.
b) So sánh AN và MD.
Một lớp học có 28 nam và 24 nữ . Có bao nhiêu cách chia đều học sinh thành các tổ với số tổ nhiều hơn 1 sao cho số nam trong các tổ bằng nhau và số nữ trong các tổ cũng bằng nhau ? Cách chia nào để mỗi tổ có số học sinh ít nhất ?
