Cho đường tròn (O; R) và điểm A cách O một khoảng 2R. Từ A vẽ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Đường thảng vuông góc với OB tại O cắt AC tại N. Đường thẳng vuông góc với OC tại O cắt AB tại M. Chứng minh: MN là tiếp tuyến của đường tròn.
Giải bởi Vietjack
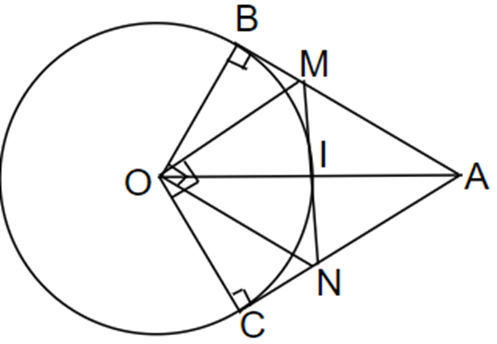
Do AB là tiếp tuyến của (O)
Þ OB ^ AB
Mà OB ^ ON
Þ AB // ON (từ vuông góc suy ra song song) hay AM // ON
Chứng minh tương tự
Þ AN // OM
Do 2 tiếp tuyến AB và AC cắt nhau tại A
Þ OA phân giác góc BAC (tính chất tiếp tuyến) hay OA phân giác góc \[\widehat {MAN}\]
Xét tứ giác AMON có: AM // ON, AN // OM, OA phân giác góc \[\widehat {MAN}\]
Þ AMON là hình thoi
Đặt I là trung điểm OA
Þ \[OI = \frac{{OA}}{2} = \frac{{2R}}{2} = R\]hay OI là bán kính của (O)
Do AMON là hình thoi
Þ OA vuông góc với MN tại I (t/c) hay OI vuông góc với MN tại I
Mà OI là bán kính của (O)
Þ MN là tiếp tuyến của (O)
Vậy MN là tiếp tuyến của (O).
Cho các số: 13,1; 13,10; 1,3.103; 1,30.103; 1,3.10−3; 1,30.10−3. Có mấy số có hai chữ số có nghĩa.
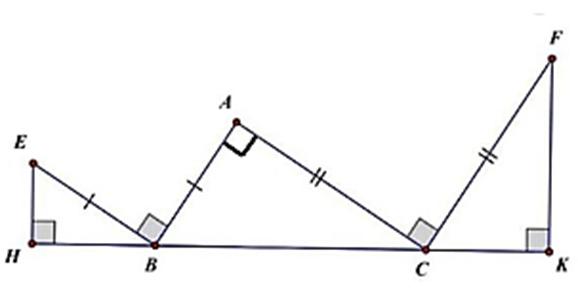
Hình vẽ bên có BE ^ BA, CF ^ CA, EH ^ BC, FK ^ BC, BE = BA và CA = CF. Chứng minh: BH = CK.
Trong không gian Oxyz, cho hai điểm A(2; 2; 1), \[B\left( {\frac{{ - 8}}{3};\frac{4}{3};\frac{8}{3}} \right)\]. Viết phương trình đường thẳng đi qua tâm đường tròn nội tiếp tam giác OAB và vuông góc với mặt phẳng (OAB).
Biết tổng các hệ của khai triển (x² + 1)n bằng 1024. Hãy tìm hệ số của x¹² trong khai triển trên.
Cho hình chữ nhật ABCD (AB > BC). Từ B kẻ BH vuông góc với AC tại H. Lấy E sao cho H là trung điểm BE, lấy Q đối xứng với C qua H. Tứ giác BCEQ là hình gì? Vì sao?
Từ điểm M nằm ngoài đường tròn (O), vẽ cát tuyến MCD không đi qua tâm O và hai tiếp tuyến MA, MB đến đường tròn (O) sao cho C nằm giữa M và D. Gọi I là trung điểm của CD. Gọi K là giao điểm của các tiếp tuyến tại C và D của đường tròn (O). Chứng minh: A, B, K thẳng hàng.
Lớp 6A có \[\frac{4}{5}\] số học sinh yêu thích môn Toán, \[\frac{7}{{10}}\] số học sinh yêu thích môn ngữ văn, \[\frac{{12}}{{25}}\] số học sinh yêu thích môn Tiếng anh. Hỏi trong 3 môn học trên môn học nào được các bạn lớp 6A thích nhất?
Từ điểm M nằm ngoài đường tròn (O), vẽ cát tuyến MCD không đi qua tâm O và hai tiếp tuyến MA, MB đến đường tròn (O) sao cho C nằm giữa M và D. Gọi I là trung điểm của CD. Chứng minh: M, A, O, I, B cùng nằm trên 1 đường tròn.
Bạn Lâm có một tờ giấy màu hình chữ nhật có chiều dài 6 dm, chiều rộng 4 dm. Bạn Lâm cắt các lá cờ hình tam giác vuông có hai cạnh góc vuông là 8cm và 10 cm. Hỏi bạn Lâm cắt được bao nhiêu lá cờ như vậy?
Tìm m để hai đồ thị hàm số y = 2x – 1 và y’ = –x + m cắt nhau tại 1 điểm có hoành độ bằng 2.
Cho nửa đường tròn (O) đường kính AB và K là điểm chính giữa cung AB. Trên cung KB lấy một điểm M (khác K; B). Trên tia AM lấy điểm N sao cho AN = BM. Kẻ dây BP song song với KM. Gọi Q là giao điểm của các đường thẳng AP, BM. Chứng minh ΔKMN vuông cân.
Có 2 đoàn xe chở xi măng vào kho, đoàn xe thứ nhất có 9 xe, đoàn xe thứ hai có 7 xe. Đoàn xe thứ nhất chở nhiều hơn đoàn xe thứ hai 148 bao xi măng. Hỏi mỗi đoàn xe chở bao nhiêu bao xi măng? Biết mỗi xe chở số bao xi măng như nhau.
Một tấm vải dài 36 m, lần đầu người ta cắt ra 16 mảnh vải, mỗi mảnh vải dài \[1\frac{1}{5}\] m, lần thứ hai người ta cắt được 6 mảnh vải dài như nhau thì vừa hết tấm vải. Hỏi mỗi mảnh vải cắt ra ở lần 2 dài bao nhiêu mét?
Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DE. Gọi I, J lần lượt là trung điểm MP, NQ. Chứng minh IJ // AE và \[IJ = \frac{1}{4}AE\].
Trong hệ tọa độ Oxy cho tam giác ABC có A(3; 5); B(1; 2) và C(5; 2). Tìm tọa độ trọng tâm G của tam giác ABC.
