Cho hình vuông ABCD có AC cắt BD tại O. M là điểm bất kỳ thuộc cạnh BC (M khác B, C). Tia AM cắt đường thẳng CD tại N. Trên cạnh AB lấy điểm E sao cho BE = CM.
a) Chứng minh: ∆OEM vuông cân.
b) Chứng minh: ME // BN.
c) Từ C kẻ CH vuông góc BN (H thuộc BN). Chứng minh rằng ba điểm O, M, H thẳng hàng.
Giải bởi Vietjack
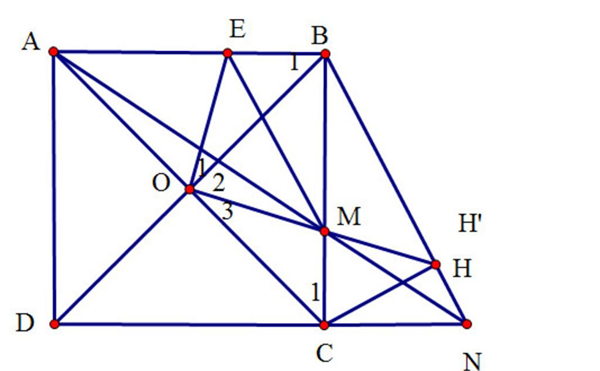
a) Xét ∆OEB và ∆OMC
Vi ABCD là hình vuông nên ta có: OB = OC
Và \[\widehat B = \widehat C = 45^\circ \]
BE = CM (gt)
Þ ∆OEB = ∆OMC (c.g.c)
Þ OE = OM và \({\widehat O_1} = {\widehat O_3}\)
Lại có: \({\widehat O_1} + {\widehat O_2} = \widehat {BOC} = 90^\circ \) vì tứ giác ABCD là hình vuông
\({\widehat O_1} + {\widehat O_2} = \widehat {EOM} = 90^\circ \) kết hợp với OE = OM
Þ ∆OEM vuông cân tại O.
b) Tứ giác ABCD là hình vuông Þ AB = CD và AB // CD
AB // CD Þ AB // CN \( \Rightarrow \frac{{AM}}{{MN}} = \frac{{BM}}{{MC}}\) (Theo định lý Ta-lét) (*)
Mà BE = CM (gt) và AB = CD Þ AE = BM thay vào (*)
Ta có: \[\frac{{AM}}{{MN}} = \frac{{AE}}{{EB}} \Rightarrow ME\;{\rm{//}}\;BN\] (theo định lý đảo Ta-lét)
c) Gọi H¢ là giao điểm của OM và BN
Từ ME // BN \[ \Rightarrow \widehat {OME} = \widehat {OH'E}\] (Cặp góc ở vị trí so le trong)
Mà \[\widehat {OME} = 45^\circ \] vì ∆OME vuông cân tại O
\( \Rightarrow \widehat {MH'B} = 45^\circ = \widehat {{C_1}}\)
Þ ∆OMC = ∆BMH¢ (g.g)
\( \Rightarrow \frac{{OM}}{{OB}} = \frac{{MH'}}{{MC}}\), kết hợp \( \Rightarrow \widehat {OMB} = \widehat {CMH'}\) (hai góc đối đỉnh)
Þ ∆OMB = ∆CMH¢ (c.g.c) \( \Rightarrow \widehat {OBM} = \widehat {MH'C} = 45^\circ \)
Vậy \(\widehat {BH'C} + \widehat {BH'M} + \widehat {MH'C} = 90^\circ \Rightarrow CH' \bot BN\)
Mà CH ^ BN (H Î BN) Þ H = H¢ hay 3 điểm O, M, H thẳng hàng (đpcm).
Rút gọn biểu thức: cos2 10° + cos2 20° + cos2 30° + ... + cos2 180°.
Cho tam giác ABC có \(\widehat {ABC} = 30^\circ \), AB = 5, BC = 8. Tính \[\overrightarrow {BA} \,.\,\overrightarrow {BC} \].
Cho tam giác ABC nhọn, đường cao AH. Gọi M, N lần lượt là hình chiếu của H lên AB và AC
a) Chứng minh AM.AB = AN.AC.
b) Chứng minh tam giác AMN đồng dạng tam giác ACB.
Cho nửa đường tròn tâm O đường kính AB, M là một điểm bất kỳ thuộc nửa đường tròn (M khác A, B). Tiếp tuyến tại M cắt các tiếp tuyến Ax và By của nửa đường tròn đó lần lượt tại C và D. Gọi K là giao điểm của BM với Ax. Tìm giá trị nhỏ nhất của tổng diện tích hai tam giác ACM và BDM.
Cho hình vuông ABCD có AC cắt BD tại O. Gọi E và F theo thứ tự là các điểm đối xứng với O qua AD và BC .
a) Chứng minh rằng các tứ giác AODE, BOCF là hình vuông
b) Nối EC cắt DF tại I. Chứng minh rằng OI ^ CD
c) Biết diện tích hình lục giác ABFCDE = 6. Tính độ dài các cạnh của hình vuông ABCD
d) Lấy K là 1 điểm bất kì trên BC. Gọi G là trọng tâm của tam giác AIK. Chứng minh G thuộc 1 đường thẳng cố định khi K di chuyển trên BC
Cho hình chữ nhật ABCD. Gọi E là điểm đối xứng của B và C.
a) Chứng minh tứ giác ACED là hình bình hành.
b) Gọi M là trung điểm của BC. Tia AM cắt tia DC tại F. Chứng minh tứ giác BDEF là hình thoi.
c) Gọi I là giao điểm của AE và DC. Tia BI cắt tia DE tại . Chứng minh \(KI = \frac{1}{6}AE.\)
Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của cạnh huyền BC. Chứng minh tam giác MAB vuông cân.
Cho hình chữ nhật ABCD. Vẽ điểm E đối xứng với B qua điểm C; vẽ F đối xứng với điểm D qua C.
a) Chứng minh tứ giác BDEF là hình thoi.
b) Chứng minh AC = DE.
c) Gọi H là trung điểm của CD, K là trung điểm của EF. Chứng minh HK // AC.
d) Biết diện tích tam giác AEF bằng 30 cm2. Tính diện tích hình chữ nhật ABCD.Cho x + y + z = 0. Rút gọn: \(A = \frac{{{x^2} + {y^2} + {z^2}}}{{{{\left( {x - y} \right)}^2} + {{\left( {y - z} \right)}^2} + {{\left( {z - x} \right)}^2}}}\).
Gọi S là tập hợp các số tự nhiên có 6 chữ số. Chọn ngẫu nhiên một số từ S, tính xác suất để các chữ số của số đó đôi một khác nhau và phải có mặt chữ số 0 và 1.
Cho tam giác nhọn ABC, \(\widehat B > \widehat C\). Gọi H là hình chiếu của A trên BC. Sắp xếp các đoạn thẳng AB, AH, AC theo thứ tự độ dài tăng dần.
Cho nửa đường tròn (O) đường kính AB. M là trung điểm OA. N là điểm bất kỳ thuộc nửa đường tròn. Qua N kẻ đường thẳng vuông góc với MN cắt các tiếp tuyến tại A và B tại C và D. Tìm vị trí của N để diện tích tam giác DMC min.
Cho tam giác ABC.
a) Hãy xác định điểm M để \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \).
b) Chứng minh rằng với mọi điểm O ta có: \(\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = 4\overrightarrow {OM} \).
Giải phương trình:
a) sin 5x + sin 8x + sin 3x = 0;
b) \(4{\cos ^3}x + 3\sqrt 2 \sin 2x = 8\cos x\).
