Cho đường tròn (O; R) có đường kính BC. Lấy A thuộc (O) sao cho AB < AC, vẽ đường cao AH của tam giác ABC.
a) Chứng minh: AH.BC = AB.AC.
b) Tiếp tuyến tại A của (O) cắt đường thẳng BC tại M. Chứng minh rằng: MA2 = MB.MC.
c) Kẻ HE vuông góc với AB (E thuộc AB) và HF vuông góc với AC (F thuộc AC). Chứng minh AM // EF.
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
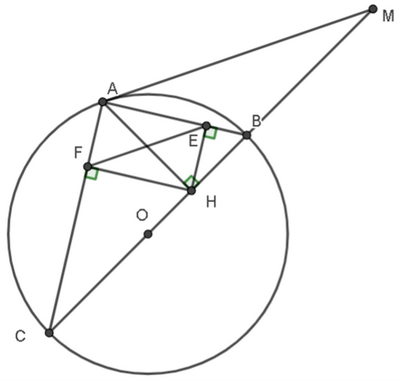
a) Ta có \(\widehat {BAC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn (O)).
Tam giác ABC vuông tại A có AH là đường cao: AH.BC = AB.AC (Hệ thức lượng trong tam giác vuông).
Vậy ta có điều phải chứng minh.
b) Xét ∆MAB và ∆MCA, có:
\(\widehat {AMB}\) chung;
\(\widehat {MAB} = \widehat {MCA}\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung).
Do đó (g.g).
Suy ra \(\frac{{MA}}{{MC}} = \frac{{MB}}{{MA}}\).
Vậy MA2 = MB.MC (điều phải chứng minh).
c) Tam giác ABH vuông tại H có HE là đường cao:
AH2 = AE.AB (Hệ thức lượng trong tam giác vuông).
Chứng minh tương tự, ta được AH2 = AF.AC.
Khi đó ta có AE.AB = AF.AC.
Xét ∆AEF và ∆ACB, có:
\(\widehat {FAE}\) chung;
\(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\) (AE.AB = AF.AC).
Do đó (g.g).
Suy ra \(\widehat {AFE} = \widehat {ABC}\) (cặp góc tương ứng) (1)
Ta có tam giác AOC cân tại O (do OA = OC = R).
Suy ra \(\widehat {OAC} = \widehat {OCA}\) (2)
Lại có \(\widehat {OCA} + \widehat {ABC} = 90^\circ \) (3)
Từ (1), (2), (3), suy ra \(\widehat {OAC} + \widehat {AFE} = 90^\circ \).
Khi đó AO ⊥ EF.
Mà AM ⊥ AO (do AM là tiếp tuyến của (O)).
Vậy AM // EF.
Cho tam giác ABC, lấy các điểm M, N, P sao cho \(\overrightarrow {MB} = 3\overrightarrow {MC} \); \(\overrightarrow {NA} + 3\overrightarrow {NC} = \vec 0\) và \(\overrightarrow {PA} + \overrightarrow {PB} = \vec 0\).
a) Tính \(\overrightarrow {PM} ,\,\,\overrightarrow {PN} \) theo \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
b) Chứng minh rằng: M, N, P thẳng hàng.
Cho tam giác ABC vuông tại A, có AH là đường cao, AM là đường trung tuyến. Qua B kẻ đường thẳng vuông góc với AM tại I cắt AC tại E.
a) Chứng minh BI.BE = 2BH.BM.
b) Chứng minh \(\frac{1}{{A{B^2}}} = \frac{1}{{B{E^2}}} + \frac{1}{{B{C^2}}}\).
Cho tam giác ABC. Gọi I là điểm trên cạnh BC sao cho 2CI = 3BI và J là điểm trên BC kéo dài sao cho 5JB = 2JC. Gọi G là trọng tâm tam giác.
a) Biểu diễn \(\overrightarrow {AB} ,\overrightarrow {AC} \) theo hai vectơ \(\overrightarrow {AI} ,\overrightarrow {AJ} \) và biểu diễn \(\overrightarrow {AJ} \) qua \(\overrightarrow {AB} ,\overrightarrow {AC} \).
b) Biểu diễn \(\overrightarrow {AG} \) theo hai vectơ \(\overrightarrow {AI} ,\overrightarrow {AJ} \).
Cho nửa đường tròn (O; R) đường kính AB, vẽ hai tiếp tuyến Ax, By với nửa đường tròn. Trên tia Ax lấy điểm E (E khác A, AE < R), trên nửa đường tròn lấy điểm M sao cho EM = EA, đường thẳng EM cắt tia By tại F.
a) Chứng minh EF là tiếp tuyến của đường tròn (O).
b) Chứng minh tam giác EOF là tam giác vuông.
c) Chứng minh AM.OE + BM.OF = AB.EF.
d) Tìm vị trí điểm E trên tia Ax sao cho \({S_{\Delta AMB}} = \frac{3}{4}{S_{\Delta EOF}}\).
Trong lớp 10C có 16 học sinh giỏi Toán, 15 học sinh giỏi Lí, 11 học sinh giỏi Hóa. Biết rằng có 9 học sinh vừa giỏi Toán và Lí, 6 học sinh vừa giỏi Lí và Hóa, 8 học sinh vừa giỏi Hóa và Toán, trong đó có 11 học sinh giỏi đúng 2 môn. Hỏi có bao nhiêu học sinh trong lớp:
a) Giỏi cả ba môn.
b) Giỏi đúng 1 môn.