Cho hai dãy ghế đối diện nhau mỗi dãy có 5 ghế. Xếp ngẫu nhiên 10 học sinh, gồm 5 nam, 5 nữ ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ.
A. \(\frac{1}{{252}}\);
B. \(\frac{1}{{945}}\);
C. \(\frac{8}{{63}}\);
D. \(\frac{4}{{63}}\).
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Số phần tử của không gian mẫu là n(Ω) = 10!
Gọi A là biến cố “Xếp 5 nam và 5 nữ ngồi đối diện nhau”
Đánh số cặp ghế đối diện nhau là: C1; C2; C3; C4; C5
• Xếp 5 bạn nam và 5 cặp ghế có 5! cách.
• Xếp 5 bạn nữ vào 5 cặp ghế có 5! cách.
Ở mỗi cặp ghê, ta có 2 cách xếp một cặp nam, nữ ngồi đối diện.
Suy n(A) = 5!.5!.25 = 460 800
\( \Rightarrow P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{460\,\,800}}{{10!}} = \frac{8}{{63}}\).
Cho tam giác đều ABC cạnh a, điểm M là trung điểm BC. Dựng các vectơ sau và tính độ dài của chúng.
a) \(\frac{1}{2}\overrightarrow {CB} + \overrightarrow {MA} \);
b) \(\overrightarrow {BA} - \frac{1}{2}\overrightarrow {BC} \);
Cho hình bình hành ABCD, giao điểm của hai đường chéo là O. Tìm mệnh đề sai trong các mệnh đề sau:
Gọi S là tập hợp tất cả các số tự nhiên có 3 chữ số được lập từ tập hợp X = {0; 1; 2; 3; 4; 5; 6; 7}. Rút ngẫu nhiên một số thuộc tập S. Tính xác suất để rút được số mà trong số đó, chữ số đứng sau luôn lớn hơn hoặc bằng chữ số đứng trước.
Trong các hàm số sau đây, hàm số nào xác định với mọi giá trị thực của x?
Cho nửa đường tròn tâm O đường kính AB. Ax là tia tiếp tuyến của nửa đường tròn (Ax và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB), từ điểm C trên nửa đường tròn (C khác A, B) vẽ tiếp tuyến CM cắt Ax tại M. Chứng minh MA2 = MQ.MB.
Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau mà các chữ số đều là số chẵn?
Tìm m để đường thẳng y = mx + 1 cắt đồ thị hàm số \(y = \frac{{x + 1}}{{x - 1}}\) tại hai điểm thuộc nhánh của đồ thị.
Ba số hạng đầu tiên theo lũy thừa tăng dần của x trong khai triển của
(1 + 2x)10 là
Cho hàm số y = (x – m)3 – 3x + m2 có đồ thị là (Cm) với m là tham số thực. Biết điểm M(a; b) là điểm cực đại của (Cm) ứng với một giá trị m thích hợp, đồng thời là điểm cực tiểu của (Cm) ứng với một giá trị khác của m. Tổng S = 2018a + 2020b bằng
Tìm m để phương trình 2sin2x – (2m + 1)sinx + m = 0 có nghiệm \(x \in \left( {\frac{{ - \pi }}{2};0} \right)\).
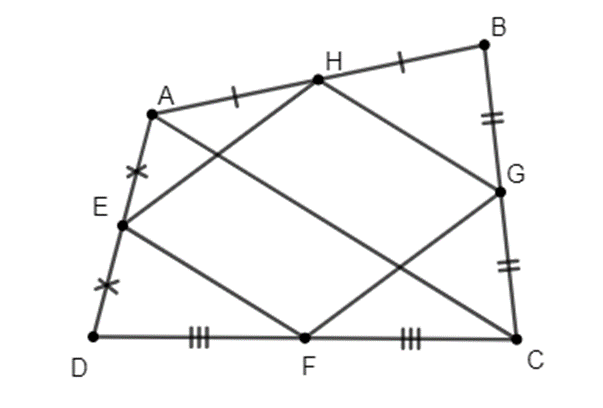
Cho tứ giác ABCD như hình dưới đây: Điểm E là trung điểm của đoạn thẳng AB. Điểm F là trung điểm của đoạn thẳng BC. Điểm G là trung điểm của đoạn thẳng DC. Điểm H là trung điểm của đoạn thẳng AD. Hỏi tứ giác EFGH là hình gì? Chứng minh điều đó.
Gọi S là tập hợp tất cả các số tự nhiên có 3 chữ số được lập từ tập X = {0; 1; 2; 3; 4; 5; 6; 7}. Rút ngẫu nhiên một số thuộc tập S. Tính xác suất để rút được số mà trong số đó, chữ số đứng sau luôn lớn hơn hoặc bằng chữ số đứng trước
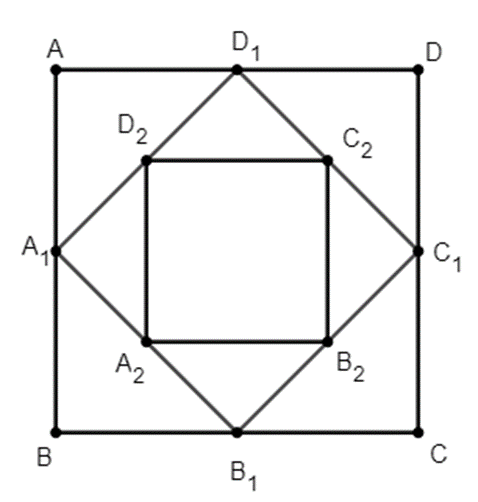
Cho hình vuông ABCD có cạnh bằng a và có diện tích S1. Nối 4 điểm A1; B1; C1; D1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích S2. Tiếp tục làm như thế, ta được hình vuông thứ ba là A2B2C2D2 có diện tích S3, … và cứ tiếp tục làm như thế, ta tính được các hình vuông lần lượt có diện tích, … , S100 (tham khảo hình bên). Tính tổng S = S1 + S2 + S3 + … + S100.
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số \(y = \left| {\frac{1}{4}{x^4} - 14{x^2} + 48x + m - 30} \right|\) trên đoạn [0; 2] không vượt quá 30. Tổng giá trị các phân tử của tập S bằng
Hỏi có bao nhiêu giá trị m nguyên trong đoạn [−2017; 2017] để phương trình logmx = 2log(x + 1) có nghiệm duy nhất?