Cho hình chóp S.ABCD có ABCD là hình thang, đáy lớn BC với BC = 2a, AD = AB = a, mặt bên (SAD) là tam giác đều. Lấy điểm M trên cạnh AB sao cho MB = 2AM. Mặt phẳng (α) đi qua M và song song với SA, BC. Xác định thiết diện của hình chóp bị cắt bởi mặt phẳng (α) và tính diện tích của thiết diện đó.
 Giải bởi Vietjack
Giải bởi Vietjack
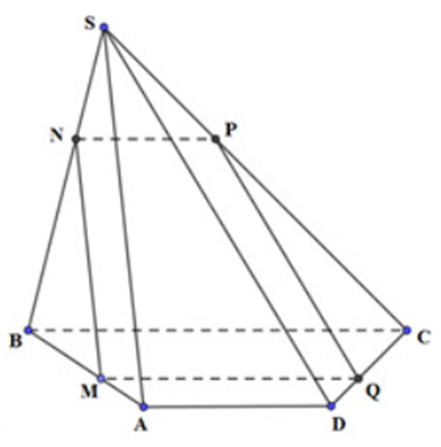
+) Dựng thiết diện:
Qua M kẻ MQ song song BC (Q ∈ DC), kẻ MN song song SA (N ∈ SB)
Qua N kẻ NP song song BC (P ∈ SC)
Khi đó, (MNPQ) là mặt phẳng qua M và song song BC, SA
⇒ (MNPQ) ≡ (α)
Thiết diện của hình chóp bị cắt bởi mặt phẳng (α) là tứ giác MNPQ.
+) Tính diện tích thiết diện:
Ta có: NP // MQ (cùng song song BC) ⇒ MNPQ là hình thang
ΔSAD đều ⇒ SA = SD = AD = a
ABCD là hình thang, MQ // BC ⇒ \(\frac{{CQ}}{{DC}} = \frac{{BM}}{{AB}} = \frac{{BN}}{{SB}} = \frac{2}{3}\)
MN // SA ⇒ \(\frac{{MN}}{{SA}} = \frac{{BM}}{{AB}} = \frac{2}{3}\) ⇒ \(MN = \frac{2}{3}SA = \frac{2}{3}a\)
NP // BC ⇒ \(\frac{{NP}}{{BC}} = \frac{1}{3}\) ⇒ \(NP = \frac{1}{3}BC = \frac{2}{3}a\) và \(\frac{{PC}}{{SC}} = \frac{{NB}}{{SB}} = \frac{2}{3}\) ⇒ \(\frac{{PC}}{{SC}} = \frac{{CQ}}{{DC}} = \frac{2}{3}\)
⇒ \(\frac{{PQ}}{{SD}} = \frac{2}{3}\) ⇒ \(PQ = \frac{2}{3}SD = \frac{2}{3}a.\)
Gọi I, J lần lượt là trung điểm của BM và CQ.
Giả sử MQ có độ dài bằng x. Khi đó, do IJ là đường trung bình của hình thang BCQM
⇒ \(IJ = \frac{{MQ + BC}}{2} = \frac{{x + 2a}}{2}\)
Do MQ là đường trung bình của hình thang IJDA ⇒ 2MQ = IJ + AD
⇔ \(2x = \frac{{x + 2a}}{2} + a\) ⇔ 4x = x + 2a + 2a ⇔ \(x = \frac{4}{3}a\)
⇒ \(MQ = \frac{4}{3}a\)
Xét hình thang MNPQ có: NP = MN = PQ = \(\frac{2}{3}a,\) \(MQ = \frac{4}{3}a\) ⇒ MNPQ là hình thang cân.
Kẻ MH, NK vuông góc với PQ (H, K ∈ PQ)
⇒ \(QH = PK = \frac{{PQ - MN}}{2} = \frac{{\frac{4}{3}a - \frac{2}{3}a}}{2} = \frac{a}{3}\)
⇒ \(MH = \sqrt {M{Q^2} - Q{H^2}} = \sqrt {{{\left( {\frac{2}{3}a} \right)}^2} - {{\left( {\frac{1}{3}a} \right)}^2}} = \sqrt {\frac{{{a^2}}}{3}} = \frac{{a\sqrt 3 }}{3}.\)
Diện tích hình thang MNPQ: \(S = \frac{1}{2}\left( {MN + PQ} \right).MH = \frac{1}{2}.\left( {\frac{2}{3}a + \frac{4}{3}a} \right).\frac{{a\sqrt 3 }}{3} = \frac{{{a^2}\sqrt 3 }}{3}.\)
Cho tam giác đều ABC tâm O, M là điểm bất kỳ trong tam giác. Hình chiếu của M xuống ba cạnh của tam giác lần lượt là D, E, F. Hệ thức giữa các vectơ \(\overrightarrow {MD} ,\overrightarrow {ME} ,\)\[\overrightarrow {MF} ,\] \(\overrightarrow {MO} \) là gì?
Tìm giá trị nhỏ nhất của hàm số \(y = 3x + \frac{4}{{{x^2}}}\) trên khoảng (0; +∞).
Trên một kệ sách có 5 quyển sách Toán, 4 quyển sách Lí, 3 quyển sách Văn. Các quyển sách đều khác nhau. Hỏi có bao nhiêu cách sắp xếp các quyển sách trên:
a) Một cách tuỳ ý?
b) Theo từng môn và sách Toán nằm ở giữa?
Từ 1 điểm A nằm ngoài đường tròn (O; R), kẻ 2 tiếp tuyến AB, AC với (O; R) (B và C là 2 tiếp điểm).
a) Chứng minh 4 điểm A, B, O, C cùng thuộc 1 đường tròn và AO ⊥ BC tại H.
b) Vẽ đường kính BD. Đường thẳng qua O và vuông góc với AD cắt tia BC tại E. Chứng minh: DC // OA.
Giải phương trình: \(3{\log _3}\left( {1 + \sqrt x + \sqrt[3]{x}} \right) = 2{\log _2}\left( {\sqrt x } \right).\)
Cho nửa đường tròn (O), đường kính AB. Kẻ 2 tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi C là một điểm thuộc tia Ax, kẻ tiếp tuyến CM với nửa đường tròn (M là tiếp điểm). CM cắt By tại D. Gọi I là giao điểm của OC và AM, K là giao điểm của OD và MB.
a) Tính \(\widehat {COD}.\)
b) Tứ giác OIMK là hình gì?
c) Chứng minh AC.BD không đổi khi C di chuyển trên Ax.
d) Chứng minh AB là tiếp tuyến của đường tròn đường kính CD.
Có bao nhiêu cặp số nguyên (x; y) thỏa mãn 0 ≤ x ≤ 2020 và log3(3x + 3) + x = 2y + 9y?
Trên một kệ sách có 5 quyển sách Toán, 4 quyển sách Lí, 3 quyển sách Văn. Các quyển sách đều khác nhau. Hỏi có bao nhiêu cách sắp xếp các quyển sách trên theo từng môn?
Cho phương trình \(\left( {2\log _3^2x - {{\log }_3}x - 1} \right)\sqrt {{5^x} - m} = 0\) (m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt?
Đồ thị hàm số y = ax3 + bx2 + cx + d có hai điểm cực trị là A(1; −7); B(2; −8). Tính y(−1).
Cho a, b, c là ba số thực dương và khác 1. Đồ thị các hàm số y = ax, y = logbx, y = logcx được cho trong hình dưới đây:
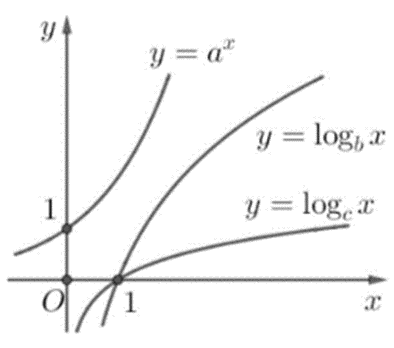
Mệnh đề nào dưới đây đúng?
Cho hàm số \(y = \frac{{2x + 1}}{{2x - 1}}\) có đồ thị (C) và đường thẳng d: y = x + 2. Tìm tọa độ giao điểm của đồ thị (C) và đường thẳng d.
Tìm tọa độ giao điểm của hai đường thẳng y = x + 2 và \(y = - \frac{3}{4}x + 3.\)
Tìm tất cả các giá trị của tham số m để hàm số y = x3 − mx2 + (2m − 3)x − 3 đạt cực đại tại điểm x = 1.