Tìm các giá trị nguyên của m để phương trình \({\cos ^2}x + \sqrt {\cos x + m} = m\) có nghiệm.
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có: \({\cos ^2}x + \sqrt {\cos x + m} = m\) ⇒ m ≥ 0.
Đặt \(\sqrt {\cos x + m} = t,t \ge 0.\)
Phương trình trở thành: \(\left\{ {\begin{array}{*{20}{c}}{{{\cos }^2}x + t = m}\\{{t^2} - \cos x = m}\end{array}} \right.\)
⇒ (cos2x – t2) + (t + cos x) = 0
⇔ (cos x + t)(cos x – t + 1) = 0
⇔ \(\left[ {\begin{array}{*{20}{c}}{\cos x = - t}\\{\cos x - t + 1 = 0}\end{array}} \right.\)
TH1: cos x = -t
⇒ \(\sqrt {\cos x + m} = - \cos x\) ⇔ \(\left\{ {\begin{array}{*{20}{c}}{\cos x \le 0}\\{{{\cos }^2}x - \cos x = m}\end{array}} \right.\)
Đặt u = cos x (-1 ≤ u ≤ 0)
Xét hàm số f(u) = u2 – u trên đoạn [-1; 0], có hoành độ đỉnh \(x = \frac{1}{2} \notin \left[ { - 1;0} \right]\) và bảng biến thiên:
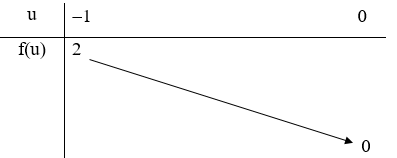
Để phương trình có nghiệm thì m ∈ [0; 2]. Vì m ∈ ℤ nên m ∈ {0; 1; 2}.
TH2: cos x – t + 1 = 0
⇔ \(\sqrt {\cos x + m} = 1 + \cos x\)
⇔ cos2x + cos x + 1 = m
Đặt v = cos x, -1 ≤ v ≤ 1. Ta có m = v2 + v + 1 = g(v)
Hàm số bậc hai g(v) có hoành độ đỉnh \(v = \frac{1}{2} \in \left[ { - 1;1} \right]\) và có bảng biến thiên:
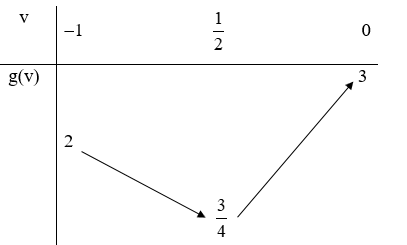
Để phương trình có nghiệm thì \(m \in \left[ {\frac{3}{4};3} \right].\) Vì m ∈ ℤ nên m ∈ {1; 2; 3}.
Vậy có tất cả 4 số nguyên m thỏa mãn bài toán.
Cho tam giác đều ABC tâm O, M là điểm bất kỳ trong tam giác. Hình chiếu của M xuống ba cạnh của tam giác lần lượt là D, E, F. Hệ thức giữa các vectơ \(\overrightarrow {MD} ,\overrightarrow {ME} ,\)\[\overrightarrow {MF} ,\] \(\overrightarrow {MO} \) là gì?
Tìm giá trị nhỏ nhất của hàm số \(y = 3x + \frac{4}{{{x^2}}}\) trên khoảng (0; +∞).
Trên một kệ sách có 5 quyển sách Toán, 4 quyển sách Lí, 3 quyển sách Văn. Các quyển sách đều khác nhau. Hỏi có bao nhiêu cách sắp xếp các quyển sách trên:
a) Một cách tuỳ ý?
b) Theo từng môn và sách Toán nằm ở giữa?
Từ 1 điểm A nằm ngoài đường tròn (O; R), kẻ 2 tiếp tuyến AB, AC với (O; R) (B và C là 2 tiếp điểm).
a) Chứng minh 4 điểm A, B, O, C cùng thuộc 1 đường tròn và AO ⊥ BC tại H.
b) Vẽ đường kính BD. Đường thẳng qua O và vuông góc với AD cắt tia BC tại E. Chứng minh: DC // OA.
Giải phương trình: \(3{\log _3}\left( {1 + \sqrt x + \sqrt[3]{x}} \right) = 2{\log _2}\left( {\sqrt x } \right).\)
Cho nửa đường tròn (O), đường kính AB. Kẻ 2 tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi C là một điểm thuộc tia Ax, kẻ tiếp tuyến CM với nửa đường tròn (M là tiếp điểm). CM cắt By tại D. Gọi I là giao điểm của OC và AM, K là giao điểm của OD và MB.
a) Tính \(\widehat {COD}.\)
b) Tứ giác OIMK là hình gì?
c) Chứng minh AC.BD không đổi khi C di chuyển trên Ax.
d) Chứng minh AB là tiếp tuyến của đường tròn đường kính CD.
Có bao nhiêu cặp số nguyên (x; y) thỏa mãn 0 ≤ x ≤ 2020 và log3(3x + 3) + x = 2y + 9y?
Trên một kệ sách có 5 quyển sách Toán, 4 quyển sách Lí, 3 quyển sách Văn. Các quyển sách đều khác nhau. Hỏi có bao nhiêu cách sắp xếp các quyển sách trên theo từng môn?
Cho phương trình \(\left( {2\log _3^2x - {{\log }_3}x - 1} \right)\sqrt {{5^x} - m} = 0\) (m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt?
Đồ thị hàm số y = ax3 + bx2 + cx + d có hai điểm cực trị là A(1; −7); B(2; −8). Tính y(−1).
Cho a, b, c là ba số thực dương và khác 1. Đồ thị các hàm số y = ax, y = logbx, y = logcx được cho trong hình dưới đây:
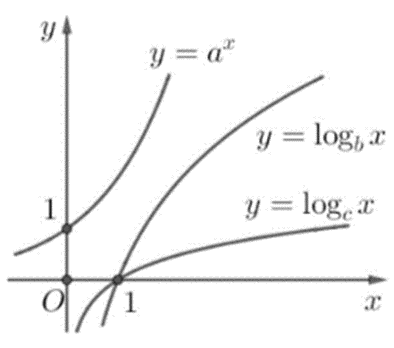
Mệnh đề nào dưới đây đúng?
Cho hàm số \(y = \frac{{2x + 1}}{{2x - 1}}\) có đồ thị (C) và đường thẳng d: y = x + 2. Tìm tọa độ giao điểm của đồ thị (C) và đường thẳng d.
Tìm tọa độ giao điểm của hai đường thẳng y = x + 2 và \(y = - \frac{3}{4}x + 3.\)
Tìm tất cả các giá trị của tham số m để hàm số y = x3 − mx2 + (2m − 3)x − 3 đạt cực đại tại điểm x = 1.