Cho đường tròn (O; R). Từ một điểm M nằm ngoài đường tròn kẻ các tiếp tuyến ME, MF đến đường tròn với (E; F là tiếp điểm). Đoạn OM cắt đường tròn (O; R) tại I. Kẻ đường kính ED của (O; R). Hạ FK vuông góc với ED. Gọi P là giao điểm của MD và FK. Chọn câu đúng:
A. Các điểm M, E, O, F cùng thuộc một đường tròn.
B. Điểm I là tâm đường tròn nội tiếp tam giác MEF.
C. Điểm I là tâm đường tròn ngoại tiếp tam giác MEF.
D. Cả A, B đều đúng.
Giải bởi Vietjack
Đáp án đúng: D
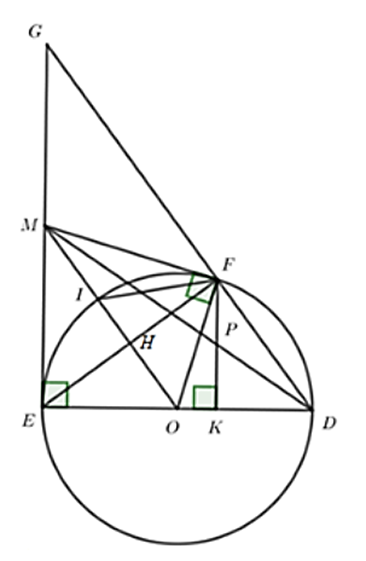
* Vì ME là tiếp tuyến của (O) nên ME vuông góc với OE, suy ra tam giác MOE nội tiếp đường tròn đường kính MO (1)
Vì MF là tiếp tuyến của (O) nên MF vuông góc với OF, suy ra tam giác MOF nội tiếp đường tròn đường kính MO (1)
Từ (1) và (2) suy ra M, E, O, F cùng thuộc một đường tròn nên A đúng
* Gọi MO ∩ EF = {H}
Vì M là giao điểm của hai tiếp tuyến ME và MF của (O)
⇒ ME = MF (tính chất) mà OE = OF = R (gt)
⇒ MO là đường trung trực của EF
⇒ MO ⊥ EF ⇒ \(\widehat {IFE} + \widehat {OIF} = 90^\circ \)
Vì OI = OF = R nên tam giác OIF cân tại O
⇒ \(\widehat {OIF} = \widehat {OFI}\) mà \(\widehat {MFI} + \widehat {OFI} = 90^\circ ;\widehat {IFE} + \widehat {OIF} = 90^\circ \)
⇒ \(\widehat {MFI} = \widehat {IFE}\)
⇒ FI là phân giác của \(\widehat {MFE}\)(1)
Vì M là giao điểm của hai tiếp tuyến ME và MF của (O)
⇒ MI là phân giác của \(\widehat {EMF}\) (tính chất) (2)
Từ (1) và (2) ⇒ I là tâm đường tròn nội tiếp tam giác MEF.
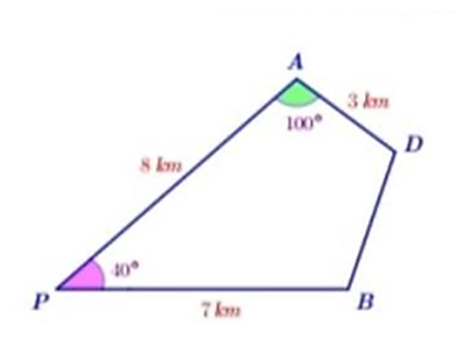
Hai bạn An và Hưng cùng xuất phát từ điểm P, đi theo hai hướng khác nhau và tạo với nhau một góc 40)° để đến đích là điểm D. Biết rằng họ dừng lại để ăn trưa lần lượt tại A và B (như hình vẽ minh hoạ). Hỏi Hưng phải đi bao xa nữa để đến được đích?
Cho mặt cầu S(O; R) và một điểm A, biết OA = 2R. Qua A kẻ cát tuyến cắt (S) tại B và C sao cho BC = \(R\sqrt 3 \). Tính khoảng cách từ O đến BC.
Cho tam giác ABC có AB = AC. Gọi I là trung điểm của BC, trên tia đối của tia IA lấy điểm D sao cho ID = IA.
a) Chứng minh ∆ABI = ∆ACI.
b) Chứng minh AC // BD.
c) Kẻ IK vuông góc với AB (K thuộc AB), IH vuông góc với CD (H thuộc CD). Chứng minh IK = IH.
Cho hình chữ nhật ABCD có AB = 3cm; BC = 5cm. Tính độ dài véctơ \(\overrightarrow {AC} \)?
Trong mặt phẳng với hệ trục tọa độ Oxy cho tam giác ABC có A(–1;1), B(1;3) và trọng tân là G\(\left( { - 2;\frac{2}{3}} \right)\). Tìm tọa độ điểm M trên tia Oy sao cho tam giác MBC vuông tại M.
Cho điểm A nằm ngoài đường tròn (O; R). Vẽ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là các tiếp điểm). Vẽ đường kính CD của đường tròn (O).
a) Chứng minh rằng: OA vuông góc BC và OA // BD.
b) Gọi E là giao điểm của AD và đường tròn (O) (E khác D), H là giao điểm của OA và BC. Chứng minh rằng: AE. AD = AH. AO.
Cho tam giác ABC có AB = AC. Lấy hai điểm D, E thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE.
a) Chứng minh \(\widehat {EAB}\) = \(\widehat {DAC}\).
b) Gọi M là trung điểm của BC. Chứng minh AM là phân giác của góc \(\widehat {DAE}\).
c) Gỉa sử \(\widehat {DAE} = 60^\circ \). Tính các góc còn lại của tam giác ADE.
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh: ∆MAB = ∆MDC.
b) Chứng minh: AB // CD và ∆ABC = ∆CDA.
c) Chứng minh: ∆BDC là tam giác vuông.
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của AC , trên tia đối của tia MB lấy điểm D sao cho MD =MB.
1) Chứng minh AD = BC.
2) Chứng minh CD vuông góc với AC.
3) Đường thẳng qua B song song với AC cắt tia DC tại N. Chứng minh tam giác ABM = tam giác CNM.
Tính diện tích hình thang có đáy lớn 54m, đáy bé bằng \(\frac{2}{3}\) đáy lớn và bằng \(\frac{3}{2}\) chiều cao.
Cho tam giác ABC vuông cân tại C, M là điểm bất kỳ trên cạnh AB. Vẽ MF vuông góc BC tại F, ME vuông góc AC tại E. Gọi D là trung điểm AB. Chứng minh rằng tam giác DEF vuông cân.
Cho đường tròn tâm (O) bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC.
Một cửa hàng có 3,125 tấn gạo. Ngày thứ nhất bán được 24%số gạo. Ngày thứ hai bán được 32% số gạo còn lại. Hỏi ngày thứ hai cửa hàng bán được bao nhiêu ki lô gam gạo?
Tính bằng cách thuận tiện: \(\frac{1}{4}:0,25 - \frac{1}{8}:0,125 + \frac{1}{2}:0,5 - \frac{1}{{10}}\).
