Cho hàm số y = f(x) xác định trên ℝ và có đạo hàm \(f'\left( x \right)\) thỏa mãn \(f'\left( x \right) = \left( {1 - x} \right)\left( {x + 2} \right)g\left( x \right) + 2018\) trong đó g(x) < 0, ∀x ∈ ℝ. Hàm số y = f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào?
 Giải bởi Vietjack
Giải bởi Vietjack
Vì \(f'\left( x \right) = \left( {1 - x} \right)\left( {x + 2} \right)g\left( x \right) + 2018\)
⇒ \(f'\left( {1 - x} \right) = \left( {1 - \left( {1 - x} \right)} \right)\left( {\left( {1 - x} \right) + 2} \right)g\left( {1 - x} \right) + 2018\)
\( = x\left( {3 - x} \right)g\left( {1 - x} \right) + 2018\)
Ta có: y = f(1 – x) + 2018x + 2019
⇒ \(y' = f'\left( {1 - x} \right).{\left( {1 - x} \right)^\prime } + 2018 = - f'\left( {1 - x} \right) + 2018\)
\( = - \left[ {x\left( {3 - x} \right)g\left( {1 - x} \right) + 2018} \right] + 2018 = x\left( {x - 3} \right)g\left( {1 - x} \right)\)
Mà g(x) < 0, ∀x ∈ ℝ, suy ra, để hàm số nghịch biến thì x(x – 3) ≥ 0
⇔ \(\left[ {\begin{array}{*{20}{c}}{x \le 0}\\{x \ge 3}\end{array}} \right.\)
Vậy hàm số y = f(x) nghịch biến trên các khoảng (-∞; 0), (3; +∞).
Biết phương trình \(\log _2^2x - 2{\log _2}\left( {2x} \right) - 1 = 0\) có hai nghiệm x1, x2. Tính x1x2.
Cho (O, R), lấy điểm A cách O một khoảng 2R. Kẻ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp điểm). Đoạn thẳng OA cắt đường tròn (O) tại I. Đường thẳng qua O và vuông góc với OB cắt AC tại K.
a) Chứng minh tam giác OBA vuông tại B và tam giác OAK cân tại K.
b) Đường thẳng KI cắt AB tại M. Chứng minh KM là tiếp tuyến của đường tròn (O).
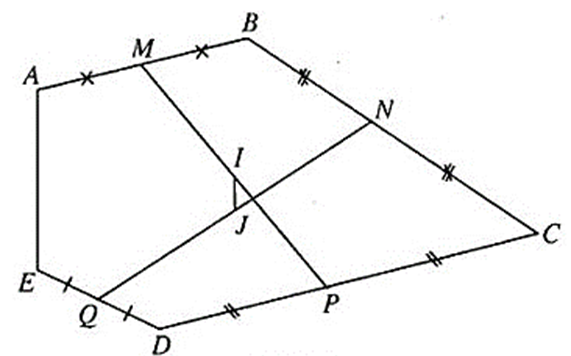
Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DE. Gọi I, J lần lượt là trung điểm MP, NQ. Chứng minh IJ // AE và AE = 4IJ.
Người ta dùng 100m rào để rào một mảnh vườn hình chữ nhật để thả gia súc. Biết một cạnh của hình chữ nhật là bức tường (không phải rào). Tính diện tích lớn nhất của mảnh vườn để có thể rào được.
Hỏi có bao nhiêu giá trị m nguyên trong [-2017; 2017] để phương trình log(mx) = 2.log(x + 1) có nghiệm duy nhất?
Cho hình chóp S.ABC có SA = SB = SC = \(a\sqrt 3 ,\) AB = AC = 2a, BC = 3a. Thể tích của khối chóp S.ABC bằng
Có 5 cái bánh, chia đều cho 8 em. Hỏi mỗi em được bao nhiêu phần cái bánh?
Tìm tất cả các giá trị của tham số m để phương trình x4 – 10x2 + m = 0 có 4 nghiệm phân biệt lập thành một cấp số cộng.
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, SA = SB = SD = a, \(\widehat {BAD} = 60^\circ .\) Góc giữa đường thẳng SA và mặt phẳng (SCD) bằng
Cho hàm số \(y = x\sqrt {4 - {x^2}} .\) Gọi M, m lần lượt là GTLN, GTNN của hàm số. Tính M + m.
Tìm tất cả các giá trị của tham số m để phương trình \(4{\left( {{{\log }_2}\sqrt x } \right)^2} - {\log _{\frac{1}{2}}}x\) + m = 0 có nghiệm thuộc khoảng (0; 1).
Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của SA, BC và P là điểm nằm trên cạnh AB sao cho \(AP = \frac{1}{3}AB.\) Gọi Q là giao điểm của SC và (MNP). Tính tỉ số \(\frac{{SQ}}{{SC}}.\)
Phương trình \(\left( {{2^x} - 5} \right)\left( {{{\log }_2}x - 3} \right) = 0\) có hai nghiệm \({x_1},{x_2}\left( {{x_1} < {x_2}} \right).\) Tính giá trị của biểu thức \(K = {x_1} + 3{x_2}.\)
Cho hình vuông ABCD cạnh a. Tính \(\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right).\left( {\overrightarrow {BC} + \overrightarrow {BD} } \right).\)