Cho tứ giác ABCD. Gọi E, F lần lượt là giao điểm của AB và CD; M, N, P, Q lần lượt là thuộc các cạnh AF, EC, BF, DE và . Khi đó MNPQ là hình gì? Khẳng định nào sau đây là đúng nhất?
A. Hình bình hành
B. Hình thang vuông
C. Hình thang cân
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
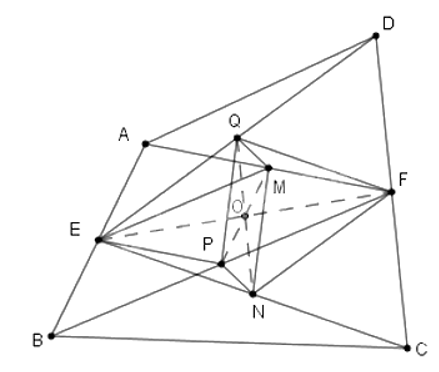
Nối EF; EP, FQ, EM, PM, QN. Gọi O là giao của QN và EF.
Xét tam giác CED ta có:
Þ NFQE là hình bình hành nên hai đường chéo QN và EF giao nhau tại trung điểm của mỗi đường. Suy ra O là trung điểm của QN và EF (1)
Xét tam giác ABF ta có:
Þ EMFB là hình bình hành nên hai đường chéo PM và EF giao nhau tại trung điểm của mỗi đường. Mà O là trung điểm của EF nên O cũng là trung điểm của PM (2)
Từ (1) và (2) suy ra: tứ giác QMNP có hai đường chéo QN, PM giao nhau tại trung điểm O mỗi đường nên QMNP là hình bình hành.
Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D. Khẳng định nào sau đây là sai?
Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D. Biết , số đo góc BDC là
Cho hình bình hành ABCD. Qua giao điểm O của các đường chéo, vẽ một đường thẳng cắt các cạnh đối BC và AD theo thứ tự E và F (đường thẳng này không đi qua trung điểm của BC và AD). Khẳng định nào sau đây là đúng?
Chu vi của hình bình hành ABCD bằng 10 cm, chu vi của tam giác ABD bằng 9 cm. Khi đó độ dài BD là
Tỉ số độ dài hai cạnh của hình bình hành là 3 : 5. Còn chu vi của nó bằng 48cm. Độ dài cạnh kề của hình bình hành là
Hãy chọn câu đúng. Cho hình bình hành ABCD, gọi E là trung điểm của AB, F là trung điểm của CD. Khi đó:
Cho hình bình hành ABCD. Gọi H, K lần lượt là hình chiếu của A, C trên đường thẳng BD. Khẳng định nào sau đây là đúng?
Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm E và F sao cho . Khẳng định nào sau đây là đúng?