Cho hình tứ diện ABCD. Gọi I, J lần lượt thuộc cạnh AD, BC sao cho IA = 2ID, JB = 2JC. Gọi (P) là mặt phẳng qua IJ và song song với AB. Khẳng định nào đúng?
A. CD cắt (P);
B. (P) // CD;
C. IJ // CD;
Giải bởi Vietjack
Đáp án đúng là: B
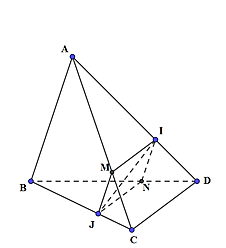
Kẻ MJ // AB, M Î AC và NI // AB, N Î BD.
Suy ra M, N, I, J đồng phẳng và (MINJ) º (P)
Thiết diện của mặt phẳng (P) và tứ diện ABCD là tứ giác MINJ, có:
Do nên suy ra MI // CD
Mà MI Ì (P) nên suy ra (P) // CD.
Do đó CD không thể cắt (P).
Ta có MI // CD mà IJ cắt MI tại I và MI, IJ Ì (P) nên suy ra IJ không song song với CD.
Lại có: nên suy ra IN // AB
Mà IJ cắt IN tại I và IN, IJ Ì (P) nên suy ra IJ không song song với AB.
Cho hai số phức z1, z2 thỏa mãn các điều kiện |z1| = |z2| = 2 và |z1 + 2z2| = 4. Tính giá trị của |2z1 − z2|.
Cho tứ diện ABCD. Gọi I, J lần lượt thuộc các cạnh AD, BC sao cho IA = 2ID và JB = 2JC. Gọi (P) là mặt phẳng qua IJ và song song với AB. Tìm thiết diện của mặt phẳng (P) và tứ diện ABCD.
Cho x > 0, y > 0 thỏa mãn xy = 6. Tìm giá trị nhỏ nhất của biểu thức:
.
Cho đoạn thẳng AB và M là điểm nằm trên đoạn AB sao cho . Tìm k trong .
Cho 4 điểm A(1; −2); B(0; 3); C(−3; 4); D(−1; 8). Ba điểm nào trong 4 điểm đã cho là thẳng hàng?
