Cho tam giác ABC cân tại A, góc và AB = 4 cm. Tính thể tích khối tròn xoay lớn nhất có thể khi ta quay tam giác ABC xung quanh đường thẳng chứa một cạnh của tam giác ABC.
 Giải bởi Vietjack
Giải bởi Vietjack
Áp dụng định lí cosin trong tam giác ABC, ta có:
Gọi H là trung điểm của BC.
Khi quay tam giác ABC quanh cạnh BC ta được 2 hình nón có chung bán kính đáy AH, đường cao lần lượt là BH và CH với:
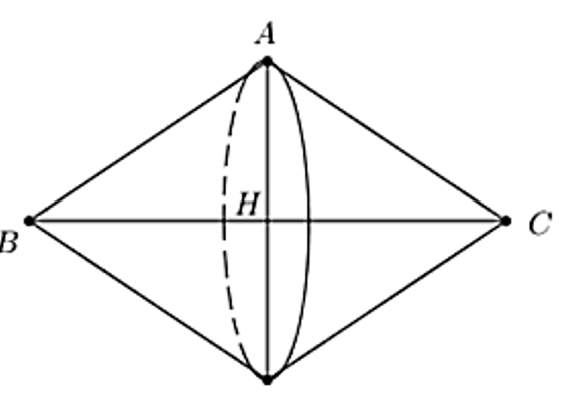
AH = AB.cos 60° = 2
Khi quay tam giác ABC quanh AB ta được khối tròn xoay như sau:
Gọi D là điểm đối xứng C qua AB, H là trung điểm của CD.
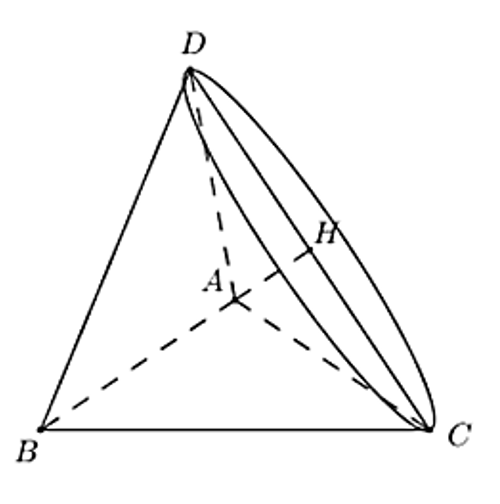
Ta có:
Do điểm B và C có vai trò như nhau nên khi quay tam giác ABC quanh AC ta cũng nhận được khối tròn xoay có thể tích bằng 16p.
Vậy thể tích lớn nhất có thể được khi quay tam giác ABC quanh một đường thẳng chứa cạnh của tam giác ABC là 16π.
Cho tam giác ABC. Hãy xác định các điểm I, J, K, L thoả các đẳng thức sau:
a)
b)
c)
d)
Cho khối chóp đều S.ABC có cạnh bên bằng a và các mặt bên hợp với đáy một góc 45°. Tính thể tích của khối chóp S.ABC theo a.
Cho hình chóp S.ABCD, gọi M là trung điểm SB và N là điểm thuộc cạnh SC sao cho SN = 2NC. Tính tỉ số .
Cho hình lập phương ABCD.A'B'C'D'. Tính góc giữa các cặp đường thẳng sau đây:
a) AB và B'C'
b) AC và B'C'
c) A'C' và B'C
Sắp xếp 6 nam sinh và 4 nữ sinh vào một dãy ghế hàng ngang có 10 chỗ ngồi. Tính số cách xếp sao cho các nữ sinh luôn ngồi cạnh nhau.
Trong mặt phẳng Oxy, cho tam giác ABC có đường cao AH, trung tuyến CM và phân giác trong BD có phương trình x + y − 5 = 0, biết H(−4; 1), . Tọa độ đỉnh A là:
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AD, BC
a) Chứng minh:
b) Xác định điểm O sao cho .
Cho hình chữ nhật ABCD, AB = 3, AD = 4. Hãy tính độ lớn của
a)
b)
Cho ∆ABC. Hãy xác định các điểm I, J, K, L thoả các đẳng thức sau:
a)
b)
c)
d)
Cho hình thang ABCD có hai đáy AB và CD với AB = 2CD. Từ C vẽ .
a) Chứng minh I là trung điểm AB và ;
b) Chứng minh .