Cho điểm M nằm ngoài đường tròn ( O; R ) sao cho OM = 2R. Từ M kẻ các tiếp tuyến MA, MB với đường tròn O (A, B là các tiếp điểm ). Kẻ đường kính AC của đường tròn (O). Gọi H là giao điểm của AB và OM.
a) Chứng minh 4 điểm : O, A, B, M cùng thuộc 1 đường tròn.
b) Tính tỉ số .
c) Gọi E là giao điểm của CM và đường tròn (O). Chứng minh HE vuông góc với BE.
Giải bởi Vietjack
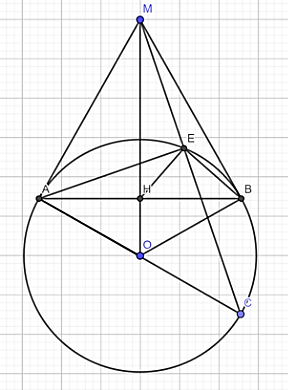
a) Vì MA, MB là tiếp tuyến của (O)
⇒ MA ⊥ OA ⇒ = 90°
⇒ MB ⊥ OB ⇒ = 90°
= 90° + 90° = 180°
⇒ OAMB là tứ giác nội tiếp
⇒ O, A, B, M cùng thuộc 1 đường tròn (đpcm)
b) Vì MA, MB là tiếp tuyến của (O) kẻ từ M
⇒ M cách đều A, B mà O cách đều A, B
⇒ MO là trung trực của AB
⇒ MO ⊥ AB tại H , H là trung điểm AB
Tam giác OAM vuông tại A có đường cao AH
Suy ra: OA2 = OH.OM
⇒ OH =
⇒
c) Áp dụng hệ thức lượng trong tam giác MAO vuông có: MA2 = MH.MO (1)
MA là tiếp tuyến nên: (cùng chắn cung AE)
Xét ∆MAE và ∆MCA có:
chung
Suy ra: ∆MAE ~ ∆MCA (g.g)
⇒ hay MA2 = MC.ME (2)
Từ (1) và (2): MC.ME = MH.MO
⇒
Xét ∆MHE và ∆MCO có:
chung
⇒ ∆MHE ~ ∆MCO (c.g.c)
⇒
⇒ 180° – = 180° – hay
Lại có: BEAC là tứ giác nội tiếp (O) do 4 điểm đều nằm trên đường tròn nên (cùng nhìn cạnh BC)
Lại có theo phần a: OBMA là tứ giác nội tiếp nên ;
Suy ra:
Lại có: (Cùng phụ với )
Mà
Suy ra:
= 90°
Vậy HE vuông góc với BE.
Một quả bóng cầu thủ sút lên rồi rơi xuống theo quỹ đạo là parabol. Biết rằng ban đầu quả bóng được sút lên từ độ cao so với mặt đất sau đó giây nó đạt độ cao và sau giây nó ở độ cao. Hỏi độ cao cao nhất mà quả bóng đạt được là bao nhiêu mét?
Cho hình bình hành ABCD có AB = 2BC. Gọi E và F theo thứ tự là trung điểm của AB, CD.
a) Chứng minh DEBF là hình bình hành.
b) Chứng minh ADFE là hình thoi.
c) Gọi M là giao điểm của DE và AF, N là giao điểm của CE và BF. Chứng minh EMFN là hình chữ nhật.
cho tam giác ABC vuông tại A. Gọi M là trung điểm của AC , trên tia đối của tia MB lấy điểm D sao cho MD = MB.
1) Chứng minh AD = BC.
2) Chứng minh CD vuông góc với AC.
3) Đường thẳng qua B song song với AC cắt tia DC tại N. Chứng minh ∆ABM = ∆CNM.
Cho hình vuông ABCD có cạnh bằng a. Gọi E là trung điểm cạnh BC, F là trung điểm cạnh AE. Tìm độ dài đoạn thẳng DF.
Một công ty cần thuê xe để chở 120 người và 6,5 tấn hàng. Nơi thuê xe có hai loại xe A và B, trong đó loại xe A có 9 chiếc và loại xe B có 8 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu đồng. Biết rằng mỗi chiếc xe loại A có thể chở tối đa 20 người và 0,5 tấn hàng; mỗi chiếc xe loại B có thể chở tối đa 10 người và 2 tấn hàng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí bỏ ra là thấp nhất?
Cho hình chóp S.ABCD đáy là hình thang (đáy lớn AB). Gọi M, N là trung điểm BC; SB. P thuộc AD sao cho 2PD = PA. Chứng minh MN // (SCD), tìm giao điểm của SA và (MNP).
Có bao nhiêu giá trị nguyên của tham số m để hàm số:
y = xác định trên ℝ?
Một mảnh vườn hình chữ nhật có chu vi là 80m và chiều rộng bằng chiều dài
a) Tính diện tích thửa ruộng đó.
b) Ở giữa mảnh vườn người ta đào một cái ao thả cá. Tính diện tích của ao,biết diện tích của ao chiếm diện tích mảnh vườn.
Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 3,6 cm HC = 6,4 cm.
a) Tính AB, AC, AH.
b) Kẻ HE vuông góc AB, HF vuông góc AC. Chứng minh AB.AE = AC.AF.
